La solution de Kaluza au problème d’Ehrenfest
Published in D. Flament, ed., Dimension, dimensions (I), Paris, Maison des sciences de l’homme, 1999

L’histoire de la relativité passe souvent par un rappel des aspects saillants de deux théories découvertes par Albert Einstein : la relativité restreinte (1905) et la relativité générale (1915). Nous nous intéressons ici à une autre théorie, sortie entre les deux : la théorie de l’espace-temps à quatre dimensions d’Hermann Minkowski. Disparu pendant les premières années de la relativité, en janvier 1909, Minkowski a eu le temps d’enclencher le processus de géométrisation du principe de relativité qui a mené à la relativité générale. Afin d’éclairer un aspect technique de ce processus, nous comparerons trois études du disque tournant, qui s’appuient chacune sur une théorie relativiste : la première théorie d’Einstein, la théorie des électrons, ou la théorie de l’espace-temps de Minkowski.

1 Hermann Minkowski et le formalisme quadridimensionnel

Pour commencer, nous voudrions rappeler quelques éléments historiques nécessaires à la compréhension du problème d’Ehrenfest en physique relativiste. Nos remarques se limiteront aux rapports de la théorie de Minkowski avec celles de ses prédécesseurs, et à la réception scientifique de son formalisme. Celle-ci sera regardée uniquement à travers notre étude bibliométrique, qui complète les lectures plus détaillées de cette réception par Pyenson (1985) et Walter (1999).

La théorie de la relativité de Minkowski, publiée le 5 avril 1908, adopta plusieurs aperçus formels avancés indépendamment par Henri Poincaré et Albert Einstein dès 1905. Minkowski souligna comme ces prédécesseurs le fait que les transformations de Lorentz forment un groupe, et que les équations de Maxwell ne changent pas leur forme sous l’action de ce groupe. Avec Poincaré, Minkowski interprétait les transformations de Lorentz comme des rotations dans un espace à quatre dimensions avec une coordonnée imaginaire. Il reprenait également la notion du quadrivecteur introduite par Poincaré.

Minkowski développa ces éléments dans une théorie de l’électrodynamique des milieux en mouvement, exprimée dans un nouveau langage vectoriel à quatre dimensions. Les scientifiques de l’époque étaient nombreux à voir dans le formalisme quadridimensionnel de Minkowski un nouveau cadre pour la théorie de la relativité. Plusieurs théoriciens, dont Arnold Sommerfeld et Max Laue, sentaient que ce cadre convenait mieux que tout autre à l’exigence de covariance des lois par rapport à la transformation de Lorentz.

La théorie de l’électrodynamique des milieux en mouvement était largement saluée à l’époque, même si on discutait certaines questions de définition. On voyait dans les équations fondamentales de Minkowski toute l’électrodynamique atomistique de l’époque. En plus, comme Laue le fit remarquer (1911b, 88), la preuve de leur respect des principes de conservation de l’énergie et du mouvement, et du principe de relativité, découlait immédiatement de leur forme.

Dans un appendice de son article, Minkowski tenta une reformulation en quatre dimensions de la mécanique relativiste. C’est ici, notamment, que Minkowski introduisit un concept qui par la suite se révéla utile aux développements dans ce domaine. Il définit ce qu’il appela die Eigenzeit, ou le temps propre, $\tau$ (1908, 100) :

$$\tau=\int d\tau=\int\sqrt{dt^{2}-dx^{2}-dy^{2}-dz^{2}}$$

Le temps propre est le paramètre de la ligne décrite par un point matériel dans l’espace-temps, ou de ce qu’on appelle la ligne d’Univers. Ces deux concepts formels–le temps propre et la ligne d’Univers–seront essentiels à la solution minkowskienne du problème d’Ehrenfest, comme nous le verrons dans la troisième section.

Une étude bibliométrique de l’ensemble des publications relativistes entre 1905 et 1915 nous permet de suivre l’évolution de l’activité des chercheurs dans ce domaine. Elle nous fournit, en même temps, une image de la pénétration du formalisme minkowskien dans la pratique des théoriciens. Mais pour construire cette image d’une manière objective, il faut distinguer entre l’ensemble d’applications du formalisme minkowskien sans rapport direct à la gravitation, et l’ensemble qui s’y rapporte. Nous introduisons donc dans notre étude un critère d’exclusion de tout article qui porte principalement sur la théorie de la gravitation.

Dans le domaine relativiste hors gravitation, nous prenons en compte tout article qui paraît sur le principe de relativité entre 1905 et 1915 dans l’une des langues de l’Europe occidentale. Notre base de données bibliographiques est construite à partir de la bibliographie de Lecat & Lecat-Pierlot (1924), avec des références supplémentaires de Hentschel (1990) et de notre propre recherche. Elle fait état de 628 articles publiés dans 131 périodiques, complétés par 60 articles provenant de volumes reliés, ou 688 articles au total. Nous établissons en outre une distinction entre les publications “minkowskiennes,” dans lesquelles l’auteur se sert du formalisme quadridimensionnel (4D), et celles où ce formalisme est absent.

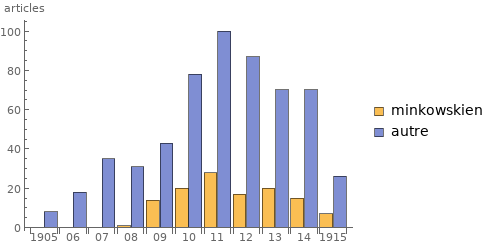
L’évolution dans le temps du nombre de publications se voit dans la figure 1, qui montre en même temps la part des articles minkowskiens (4D) par rapport au nombre d’articles relativistes où ce formalisme est absent. Elle représente dix-huit pour cent de l’ensemble pour la période de 1905 à 1915, et même vingt-trois pour cent pour la période entre janvier 1910 et décembre 1915.

En ce qui concerne les périodiques, presqu’un article sur deux paraît dans un journal allemand (303 sur 628), mais presque trois articles minkowskiens sur quatre paraissent en Allemagne dans la même période (74 sur 111). La domination des périodiques allemands se compare avec le nombre de chercheurs relativistes en Allemagne (chercheurs “allemands”) : on compte 98 chercheurs allemands parmi les 241 chercheurs répertoriés dans tous les pays. Si on regarde l’ensemble des auteurs minkowskiens, on trouve une proportion un peu plus grande de chercheurs allemands, ou vingt-trois sur quarante-huit. Dans les deux cas, l’Allemagne compte bien davantage de chercheurs que les autres pays.

L’analyse disciplinaire nous révèle que lorsque les journaux de physique publient presque la moitié des articles relativistes (294 sur 628) ou minkowskiens (56 sur 111), les journaux de mathématiques, pour leur part, accueillent un article relativiste sur douze, et un article minkowskien sur cinq.

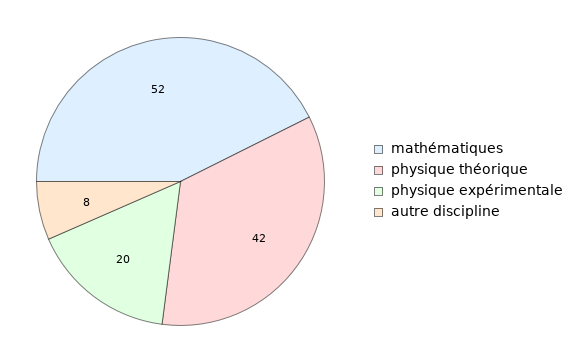
Une image de la structure disciplinaire de ces publications est formée au moyen d’une corrélation avec l’affiliation professionnelle des auteurs. Le critère principal d’affiliation est institutionnel : pour les besoins de cette étude, l’intitulé de la chaire universitaire détermine l’appartenance disciplinaire de tous ceux qui en dépendent, y compris les enseignants non titulaires. Le nombre de contributions de mathématiciens, de physiciens (théoriciens et non théoriciens), et de chercheurs appartenant à d’autres disciplines (y compris les chercheurs sans affiliation) est comparé (Figure 2) pour l’ensemble d’articles sur le principe de relativité hors gravitation et le sous-ensemble des applications minkowskiennes (Figure 3). On sait d’ailleurs que dans le domaine de la relativité hors gravitation, neuf articles sur dix sont rédigés par un mathématicien ou par un physicien pendant la période de 1905 à 1916. Les mathématiciens sont responsables d’un article sur quatre dans ce domaine, et de deux applications minkowskiens sur cinq. Ils produisent presqu’autant d’articles sur la relativité (183) que les physiciens théoriciens (223) ou les physiciens non théoriciens (221), et dominent le champ des applications minkowskiennes dans la théorie de la relativité hors gravitation, avec 52 publications, contre 42 et 20, respectivement.

Figure 1. Articles sur la relativité (hors gravitation), 1905–1915 ($N=688$).

Figure 2. Distribution d’articles relativistes par discipline, 1908–1915 ($N=688$).

Figure 3. Distribution d’articles minkowskiens par discipline, 1908–1915 ($N=122$).

2 Le mouvement rigide de Born

Dès son introduction, la théorie d’Einstein dut faire face aux incertitudes par rapport à sa cohérence interne, lorsque les physiciens essayèrent de déterminer les limites de son domaine de validité. Le physicien Walter Kaufmann, par exemple, observa que la contrainte imposée par la théorie de Lorentz-Einstein aux référentiels inertiels voulait dire que son pouvoir d’explication était assez réduit dans le monde réel. Einstein lui-même reconnut que si le principe de relativité s’appliquait à l’électrodynamique, on ne disposait toujours pas d’une dynamique relativiste du corps rigide en mouvement rectiligne (1907a, 381).

Nous avons mentionné en amont comment la démarche de Minkowski en électrodynamique aboutit à une tentative de reformulation quadridimensionnelle de la mécanique, à travers la notion du temps propre. La mécanique classique, disait-il alors, n’était que le cas limite de la nouvelle mécanique caractérisée par le groupe de Lorentz, quand on faisait grandir son paramètre jusqu’à l’infini (1908, 513-4; 1909, 105).

Cette relation de limite entre l’ancienne et la nouvelle mécanique rappelait chez quelques savants celle établie en géométrie par Felix Klein aux début des années 1870. S’appuyant sur les travaux du mathématicien de Cambridge Arthur Cayley en géométrie projective métrique, Klein découvrit comment élaborer le rapport entre la géométrie euclidienne et ce qu’il appelait la géométrie elliptique et hyperbolique (Cayley 1859; Klein 1871). En bref, la géométrie euclidienne devint un cas à la limite de la géométrie non euclidienne ; il s’agissait de prendre la limite à l’infini du paramètre de la formule de la distance, dont la réciproque de signe opposé était la courbure scalaire de Riemann (Bonola 1955, 162-3).

L’analogie entre l’ancienne et la nouvelle mécanique, d’une part, et entre la géométrie euclidienne et non euclidienne, d’autre part, à travers un rapport à la limite, était souvent invoquée dans les exposés de la relativité d’avant-guerre ; ce phénomène s’explique en partie par une connaissance généralisée des principes du programme d’Erlangen. Ces principes étaient bien présents à l’esprit des chercheurs à Göttingen, et en particulier, à celui de Max Born.

Après des études à Zurich avec Hurwitz, et à Göttingen avec Hilbert, Klein, Minkowski et Voigt, Born passa sa thèse avec Carl Runge en mathématiques appliquées en janvier 1907. Il étudia la physique expérimentale à Cambridge et à Breslau (Wrocklaw), et devint l’assistant de Minkowski quelques semaines avant la mort de celui-ci.

Pendant l’été 1909, Born mit l’analogie de la géométrie non euclidienne à l’œuvre dans une lettre au physicien théoricien Paul Ehrenfest, afin de le persuader de la validité générale du principe de relativité :

In mehr als einjähriger Arbeit habe ich mich nämlich davon überzeugt, daß das sog. "Relativitätsprincip" der Ausdruck für eine verallgemeinerte Kinematik ist, die die gewöhnliche in allen ihren Zweigen als Grenzfall in sich enthält und zu ihr etwa in demselben Verhältnis steht, wie eine hyperbolische Caylei’sche Maßbestimmung (nichteuklidische Geometrie mit negativem Krümmungsmaß) zu der gewöhnlichen euklidischen Geometrie.

L’adoption de cette interprétation du principe de relativité–en tant qu’une cinématique généralisée à travers la géométrie de Cayley-Klein–se fait sans ambages chez Born, formé (comme Ehrenfest) en mathématiques et en physique à Göttingen.

La cinématique généralisée dont parlait Born prenait la forme d’une définition covariante du corps rigide, qui s’appuyait sur des contraintes formelles sur son mouvement dans l’espace-temps. En bref, Born définit le corps rigide comme celui dont les points correspondaient à un faisceau de lignes d’Univers avec une distance invariante entre elles dans l’espace-temps, où la distance entre lignes d’Univers se mesurait sur des hyperplans du genre espace, orthogonaux au vecteur tangent. Born présenta son travail à la réunion de l’Association allemande à Salzburg en septembre 1909.

À la fin du mois, Ehrenfest critiqua la définition de Born dans les pages du Physikalische Zeitschrift ; il en releva deux conséquences. Il constata d’abord qu’un observateur au repos trouverait que les éléments tangents à la circonférence d’un cylindre rigide (au sens de Born) en rotation uniforme serait plus courts que les mêmes éléments d’un cylindre au repos, tel que $2\pi R^{\prime}<2\pi R$. Ehrenfest observa ensuite que le rayon du cylindre en rotation ne se modifierait pas ($R^{\prime}=R$), parce qu’il n’y a pas de composante de mouvement dans ce sens (en accord avec l’interprétation canonique de la transformation de Lorentz pour les cadres de référence en mouvement uniforme rectiligne). Les deux énoncés, souligna Ehrenfest, se contredisent.

L’argument d’Ehrenfest ne concernait pas la théorie d’Einstein, dont le domaine de validité se limitait au mouvement uniforme de translation. En revanche, il mettait explicitement en cause la définition du corps rigide de Born et, à travers elle, la théorie de l’espace-temps de Minkowski dans son application au mouvement non uniforme. Ehrenfest souligna donc le contraste entre le système de mesure d’un observateur au repos (au sens d’Einstein) et la métrique minkowskienne, qui introduisait, selon Ehrenfest, “un continuum d’observateurs infinitésimaux.”

Sans connaître l’article d’Ehrenfest, l’ancien Privatdozent à Göttingen Gustav Herglotz, alors professeur de mathématiques à Leipzig, fit aussi une étude de la définition de Born. Se servant du formalisme quadridimensionnel, Herglotz interpréta la transformation de Lorentz comme un déplacement dans l’espace hyperbolique, et il trouva la définition de Born inadéquate, parce qu’un corps rigide au sens de Born n’a que trois degrés de liberté en général, au lieu des six du corps rigide en mécanique classique. Néanmoins, Herglotz considérait qu’un corps rigide au sens de Born pourrait tourner autour d’un point avec une vitesse constante.

En fait, l’étude de Herglotz, à la différence de celle de Fritz Noether, ne prit pas en considération le cas précis soulevé par Ehrenfest. Ancien élève d’Aurel Voss à Munich, Noether n’utilisa pas le formalisme de Minkowski, alors peu connu. Le problème avec la définition de Born, selon Noether, c’était qu’elle ne permettait que la rotation uniforme et la translation.

Dans une lettre à Herglotz (publiée aux Annalen der Physik), le mathématicien de Padoue Tullio Levi-Cività remarqua à propos de la définition de Born que du “point de vue physique”, la considération des corps rigides dans la théorie de la relativité nécessitait un postulat de l’homogénéité de l’espace (1910, 240). Autrement dit, Levi-Cività croyait, semble-t-il, que le mouvement rigide de Born n’était pas compatible avec une courbure variable de l’espace.

C’est ainsi que, pour la première fois dans le contexte relativiste, et en rapport direct avec une étude minkowskienne, la possibilité d’une courbure variable de l’espace fut abordée. La lettre de Levi-Cività lui-même ne fit que signaler que les corps rigides de Born ne pouvaient exister dans un espace riemannien. Comme nous le verrons, trois études prêtèrent confort à cette thèse, en montrant–implicitement–sa validité par rapport au cas du disque tournant.

3 La géométrie du disque tournant

Deux physiciens à Cambridge, Harold Donaldson et Gilbert Stead publièrent deux études du problème du disque tournant, dont seulement la seconde fit intervenir la géométrie non euclidienne. Ils commencèrent leur première étude avec une simplification du problème posé par Ehrenfest ; en effet, ils aplatirent son cylindre afin d’en faire un disque. Comme Ehrenfest, ils supposèrent que la longueur des éléments tangents à la rotation rétrécit, lorsque celle des éléments dans le sens radial reste inchangée par rapport aux mêmes éléments au repos.

La contraction des éléments tangents à la rotation, selon Donaldson et Stead, entraînait des tensions dans le disque, qui prenait donc la forme d’une coupe. Or, l’idée selon laquelle l’accélération d’un disque au repos à un état de rotation uniforme induisait des tensions avait été suggérée par Planck (1910), mais les deux physiciens de Cambridge semblaient ignorer ce travail. Ils supposèrent d’ailleurs que la distance de la surface intérieure de la coupe à l’axe de rotation était égale à $r(1-v^{2}/c^{2})^{-1/2}$, où r signifie le rayon du disque au repos, et ils considéraient (comme Ehrenfest) la géométrie du disque uniquement du point de vue d’un observateur au repos. Leur “solution quantitative” du problème (modifié) d’Ehrenfest nécessitait un changement dans la forme du disque, qui était observable, au moins en principe (1910, 92, 95).

L’analyse de Donaldson et Stead suscita des critiques acerbes de la part des chercheurs en Angleterre et en Allemagne. Au cours d’un échange polémique avec Ehrenfest sur la possibilité de mettre un disque en rotation rigide, un physicien de la firme optique Leitz à Wetzlar, Vladimir von Ignatowsky se demanda pourquoi la surface du disque serait déformée. Le raisonnement de Donaldson et Stead, décida-t-il, ne pouvait pas être valide. En Angleterre, la supposition d’une déformation du disque était critiquée par un maître de conférences de physique à Sheffield, W. F. G. Swann. La déformation du disque en dehors du plan de rotation, selon Swann, contredisait le principe de relativité (1911, 342).

Trois mois après la publication de leur premier essai, Donaldson et Stead révisèrent leur analyse de la géométrie du disque tournant. Ils retinrent la coupe inventée auparavant, mais ils décidèrent qu’il s’agissait d’un modèle de la vraie géométrie du disque. Car, si le disque ne se déforme pas quand on le met en rotation, alors

we should have, owing to the lessening of the circumference and the invariability of the radius, a change in the value of the “constant” $\pi$, whereby we are transformed to a “real curved space.” This cuplike representation of our disk is a method of representing the contracted disk in ordinary space, and the results obtained by considering it will still hold good, even if the disk really remain plane.

La rectification de la géométrie du disque ne changea en rien leurs calculs, parce qu’ils assumèrent partout que la surface de la coupe dans l’espace ordinaire était une image adéquate de la véritable géométrie non euclidienne du disque tournant.

Cependant, l’avantage qu’ils tiraient de la géométrie non euclidienne était réel, parce qu’ils ne supposèrent plus que les éléments du disque sortent du plan de rotation. Ils éliminèrent ainsi la cible des critiques mordantes lancées à leur encontre par von Ignatowsky et Swann, comme nous l’avons vu plus haut.

L’adoption de la géométrie non euclidienne chez Donaldson et Stead s’accompagnait d’une autre innovation par rapport à leur premier essai. Auparavant, ils suivirent la même méthode qu’Ehrenfest, qui ne prit en considération que le point de vue d’un observateur au repos. Leur second essai introduisit le point de vue d’un observateur en rotation. À travers cette démarche, toutefois, le modèle de la coupe se révéla insatisfaisant. D’après le modèle, la longueur d’une circonférence du disque en rotation se contracte par rapport à celle du disque au repos. Or, selon Donaldson et Stead, les observateurs au repos et ceux en rotation uniforme s’accordent sur le nombre de révolutions accomplies pendant une durée déterminée, ce qui veut dire que l’unité du temps sur la coupe s’agrandit en proportion inverse à la contraction de la circonférence (1911, 320).

Ce dernier résultat s’accordait d’une façon qualitative avec l’interprétation orthodoxe du comportement des horloges idéales dans un système de référence en mouvement uniforme rectiligne. Donaldson et Stead s’en félicitaient, en disant qu’avec le modèle de la coupe on disposait d’une méthode “directe et très fiable pour passer des unités de longueur aux unités de temps”. Le modèle de la coupe, reconnurent-ils toutefois, ne se prête pas à la démonstration du phénomène de contraction des longueurs, mais pour eux il s’agissait d’un défaut mineur, parce qu’une telle démonstration avait été établie déjà ailleurs pour le cas du mouvement rectiligne. Leur opinion de la validité de la théorie de la relativité ne changea pas–cette théorie s’appliquait sans contradiction au cas de rotation uniforme.

À Londres, le professeur de mathématiques appliquées, et théoricien de l’atome John W. Nicholson applaudit leur solution “ingénieuse” du problème d’Ehrenfest, à travers la déformation du disque tournant. En effet, Nicholson affirma que c’était là la seule façon de représenter les phénomènes en “géométrie ordinaire”. Nicholson reprit un travail de Swann, qui avait cherché en vain une transformation qui permettrait de passer des équations de Maxwell en coordonnées stationnaires aux coordonnées en rotation uniforme (Swann 1911). Plus habile que Swann, Nicholson suivit, lui aussi, la méthode introduite par Joseph Larmor et Hendrik-Antoon Lorentz pour le cas de mouvement uniforme rectiligne. Son étude du disque tournant lui fit croire, comme Donaldson et Stead, que sa géométrie est non euclidienne. Mais pour garder intacte la forme des équations de Maxwell, il dut introduire une transformation différentielle de la coordonnée temporelle, en accord avec celle du système stationnaire au premier ordre en $v/c$. Nicholson renonça aussitôt sa tentative de dérivation du principe de relativité à partir des coordonnées en rotation, puisqu’il croyait qu’une transformation “plus complète” des coordonnées était hors de portée (1912, 825).

Il semble bien que Nicholson ne connaissait pas la solution au problème d’Ehrenfest proposée en septembre 1910 par Theodor Kaluza. Fils de Max Kaluza, le Geheimrat professeur de langue et littérature anglaises à Königsberg (Kaliningrad), Theodor Kaluza obtint un doctorat à Königsberg sous la direction de W. Franz Meyer en 1907. Il continua ses études avec Minkowski à Göttingen, avant de revenir à Königsberg, où il reçut l’habilitation en mathématiques pures et appliquées en 1909 (Folkerts 1977; Laugwitz 1986).

Tout comme les physiciens de Cambridge, Kaluza regarda le problème du disque tournant à travers la géométrie analytique. À partir des études du mouvement rigide d’Herglotz et de Noether, il voyait le besoin de revoir les fondements géométriques du mouvement dans l’espace-temps, comme il remarqua au début de son analyse :

Dem Relativitätsprinzip gemäß wird man als “Eigengeometrie” eines irgendwie bewegten Körpers (zu einer bestimmten Eigenzeit) im allgemeinen die Geometrie des betreffenden Orthogonalschnittes des Weltlinienbündels anzusehen haben. [1910, 977]

En ce qui concerne les corps en mouvement uniforme rectiligne, Kaluza observa que cette géométrie est euclidienne, mais Herglotz et Noether lui avaient montré que la géométrie des corps en rotation rigide est différente : sur le disque tournant, les lignes d’Univers des points fixes se laissent représenter par des hélices non orthogonales dans l’espace-temps à trois dimensions. La notion de “géométrie propre” (Eigengeometrie) ne s’applique pas au disque entier, précisa-t-il. Toutefois, continua Kaluza, elle a lieu lorsqu’il s’agit de la géométrie locale d’un point du disque tournant.

L’analyse de Kaluza surmonta à deux problèmes, à savoir la détermination de la géométrie intrinsèque du disque tournant, et de ce qu’il appela les “lois de comparaison du temps”. Kaluza ne fournit pas la métrique qui correspondait à son analyse d’une façon explicite. Néanmoins, nous pouvons la reconstruire à partir des conditions énoncées, dont l’essentielle est celle-ci : les droites hélicoïdales décrites par un point fixe du disque tournant dans l’espace-temps doivent coïncider avec les droites de la géométrie spatiale qui traversent ce même point. Les géodésiques spatiales du disque tournant, autrement dit, sont les projections des lignes d’Univers décrites par les points du disque sur un plan normal à l’axe de rotation. Il s’agit donc d’une métrique de la forme $ds^{2}=c^{2}dT^{2}-d\ell^{2}$, où dT désigne le temps local de l’observateur sur le disque tournant, et $d\ell$ signifie la longueur d’arc. L’expression pour la longueur d’arc elle-même est compatible avec une application de la contraction de FitzGerald-Lorentz, ce que Kaluza ne dit pas. En coordonnées polaires, Kaluza exprima la longueur d’arc

$$s=\int\sqrt{1+\frac{r^{2}}{1\pm r^{2}}\left(\frac{d\varphi}{dr}\right)^{2}}dr,$$

où l’ambiguïté de signe reflète la possibilité mathématique de vitesses plus rapides que la vitesse de propagation de la lumière. Il l’identifia aussitôt comme celle d’une géométrie lobachevskienne particulière, et laissa à ses lecteurs le soin de tirer leur propre conclusion vis-à-vis du problème d’Ehrenfest, qu’il ne mentionna jamais. À partir de l’expression de la longueur d’arc, la détermination de l’équation des géodésiques est un exercice de géométrie analytique ; sur un plan normal à l’axe de rotation, Kaluza trouva la formule

$$\varphi-\varphi_{0}=\arccos\frac{r_{0}}{r}\pm r_{0}\sqrt{r^{2}-r_{0}^{2}},$$

où $r_{0}$ serait la distance à l’origine, ce qui coïncide dans ce cas avec l’axe de rotation.

Si l’on cherche la droite qui passe entre deux points, observa Kaluza, on tombe sur l’expression “connue en astronomie comme ‘l’équation de Kepler”’,

$$\Phi=\Psi\pm R\sin\Psi.$$

Kaluza a-t-il donc considéré que la géométrie riemannienne du disque tournant se rapportait à la loi des forces centrales, ou aux forces centrifuges de la mécanique classique ? Dans ce sens, Einstein aurait été un précurseur, lorsqu’il postula l’équivalence du champ de gravitation avec le champ d’accélération. Mais Einstein ne postula cette équivalence qu’à propos des systèmes de références uniformément accélérés en mouvement rectiligne (1907, 454). Chez Kaluza, de toute façon, la géométrisation des forces reste implicite, et une fois données les formules de la longueur d’arc et des géodésiques, Kaluza termina son étude de la géométrie spatiale du disque tournant.

Il lui restait, bien sûr, la question du temps. Kaluza observa d’abord que le temps de l’observateur en rotation dépend de son chemin, ce qui fait qu’une horloge synchronisée de proche en proche autour d’un circuit fermé montre une “erreur de fermeture” (Schlußfehler) par rapport au temps propre. Kaluza précisa que l’erreur de fermeture est égale à l’intégrale curviligne

$$\int\frac{r^{2}d\varphi}{\sqrt{1\pm r^{2}}}.$$

Si nous introduisons les constantes supprimées par Kaluza, cette expression s’évalue à $2\omega A/c^{2}$ au premier ordre d’approximation, où A signifie l’aire de la projection du circuit sur le plan normal à l’axe de rotation.

Le sens de l’expression de l’erreur de fermeture se laisse reconstruire de la façon suivante. Prenons le carré de la longueur d’arc s, et réécrivons-le dans la forme :

$$d\ell^{2}=dr^{2}+\frac{r^{2}d\varphi^{2}}{(1-r^{2}\omega^{2}/c^{2})}.$$

Alors par substitution, la métrique spatio-temporelle implicite de Kaluza, $ds^{2}_{K}$, s’écrit :

$$ds^{2}_{K}=c^{2}dT^{2}-dr^{2}-\frac{r^{2}d\varphi^{2}}{(1-r^{2}\omega^{2}/c^{2})}.$$

Le temps local sur le disque tournant, dT, s’exprime dans les coordonnées du laboratoire dt à travers une transformation. Il s’agit d’une méthode précoce, dont on se servira plus tard en relativité générale (Einstein l’employa dans un cahier vers 1912, voir Einstein 1995, Doc. 10, p. 8). Réécrivons la métrique de Minkowski en coordonnées polaires ($r^{\prime}$, $\varphi^{\prime}$, $t^{\prime}$),

$$ds^{2}=c^{2}dt^{\prime 2}-dr^{\prime 2}-r^{\prime 2}d\varphi^{\prime 2},$$

et désignons les coordonnées stationnaires du système tournant $r$, $\varphi$, $t$. Introduisons la transformation $r^{\prime}=r$, $\varphi^{\prime}=\varphi+\omega t$, $t^{\prime}=t$, pour obtenir la métrique en coordonnées inertielles, désignée $ds^{2}_{I}$ :

$$ds^{2}_{I}=(c^{2}-\omega^{2}r^{2})dt^{2}-2\omega r^{2}d\varphi dt-dr^{2}-r^{2}d\varphi^{2}.$$

L’équivalence des métriques $ds^{2}_{K}$ et $ds^{2}_{I}$ nous permet d’écrire une expression différentielle pour le temps local :

$$dT=\sqrt{1-\frac{\omega^{2}r^{2}}{c^{2}}dt+\frac{\omega r^{2}/c^{2}}{\sqrt{1-\omega^{2}r^{2}/c^{2}}}d\varphi}.$$

Cette différentielle n’est pas exacte, mais elle respecte l’isotropie locale de la propagation de la lumière pour les observateurs en rotation (voir Langevin 1935 ; Dieks 1991). Le premier terme à droite de l’égalité est le temps propre en coordonnées polaires. Le second terme est une ‘correction’ spatiale liée à la rotation ; elle est égale à l’erreur de fermeture de Kaluza, pourvu qu’on choisisse les constantes telles que $\omega=c=1$, et $r\omega<c$.

L’existence d’une erreur de fermeture signala à Kaluza la possibilité de mettre en évidence la rotation terrestre. Un signal optique envoyé autour de la Terre à l’équateur, prédit-il, montre une erreur de fermeture de vingt microsecondes. Il prit soin de préciser qu’une confirmation de l’effet ne mettrait pas en cause la théorie de la relativité.

Publié dans le Physikalische Zeitschrift sous un titre générique–“La théorie de la relativité”–l’article de Kaluza n’attira pas l’attention des savants. Cette indifférence apparente s’explique sans difficulté par des circonstances internes et externes. La concision extrême de son exposé (y compris l’argument, l’expression mathématique et l’absence de références), et sa considération peu orthodoxe de vitesses au-dessus de celle de la propagation de la lumière exigeaient de ses lecteurs un niveau extraordinaire de raffinement mathématique, d’attention, et de tolérance. Une indulgence de ce genre aurait été accordée difficilement à un jeune Privatdozent de mathématiques sans la moindre publication en physique, et apparemment sans soutien dans la communauté de physique théorique.

La réception des idées de Kaluza a sans doute souffert aussi du déclin d’intérêt dans le problème de rotation rigide. Quelques mois avant la publication de l’article de Kaluza, et dans la même revue, Max Planck fit face au problème révélé par Ehrenfest. Planck annonça que le concept du corps rigide était une “abstraction” dont la théorie de la relativité n’avait pas besoin, parce que la déformation d’un corps accéléré se laissait aborder comme un problème d’élasticité. Évidemment, par rapport à la théorie de l’élasticité, ce qu’un commentateur appela la “géométrie supérieure” (higher geometry) de la solution de Kaluza aurait semblé trop exotique même aux physiciens théoriciens les plus adroits en mathématiques.

4 Discussion

Les différences entre les trois cas soulevés ici sont manifestes, d’abord dans le choix de cadre théorique, d’où chacun puisait les concepts relativistes et mathématiques à mettre en œuvre, et ensuite dans l’habilité du maniement de ces concepts. Cette diversité théorique pose un obstacle à qui veut comprendre ces trois cas par rapport au seul cadre théorique de la relativité restreinte. En ce qui concerne le problème de rotation uniforme, un tel cadre est absent jusqu’aux années 1920. La comparaison des contributions de Donaldson et Stead avec l’“interprétation einsteinienne”, par exemple, relève de l’anachronisme. De même, pour la période qui nous concerne, on ne peut parler d’un canon d’interprétation pour le cas de la rotation uniforme, ni par rapport à la théorie des électrons, ni par rapport à la théorie de l’espace-temps. Avec cette mise en garde, tentons tout de même de situer chacun des trois cas par rapport aux cadres théoriques de l’époque, sans perdre de vue les circonstances des individus.

Les deux articles des physiciens de Cambridge ne révèlent aucune connaissance des techniques de la théorie des électrons, du formalisme minkowskien, ou de la géométrie riemannienne. Sans doute, leur formation ne leur laissa pas d’alternative à la méthode adoptée au début, c’est-à-dire, l’étude de la géométrie d’une surface dans l’espace ordinaire. Néanmoins, dans les deux cas, ces chercheurs trouvèrent que la géométrie spatiale du disque tournant est non euclidienne. Donaldson et Stead arrivèrent à cette conclusion à partir du fondement étroit des conventions de mesure einsteiniennes pour des référentiels en mouvement uniforme rectiligne, sans l’aide de la relativité minkowskienne ou de la géométrie riemannienne.

À la différence de Donaldson et Stead, John Nicholson avait une formation et une culture mathématique qui le mettaient parmi les meilleurs théoriciens anglais de l’époque. Sa connaissance de la théorie des électrons et de la géométrie riemannienne l’a aidé à développer la géométrie intrinsèque du disque tournant. Il avait entendu parler sans doute de la théorie d’Einstein et du formalisme minkowskien, sans s’en servir lui-même. Nous avons vu que Nicholson était incapable de relier convenablement son expression de la géométrie intrinsèque du disque à la coordonnée temporelle. L’application de la métrique minkowskienne aurait suffit dans ce cas, mais à l’évidence, Nicholson ne connaissait pas cette technique.

Le travail de Kaluza fit abstraction de la matière du disque, pour n’en retenir que son aspect cinématique. Il est donc naturel que la théorie des électrons n’y figure pas. En ce qui concerne la théorie d’Einstein, elle n’y paraît pas non plus, même si la métrique spatiale de Kaluza correspond à la convention de mesure d’Einstein. Kaluza fit preuve d’une aisance dans l’application de la théorie de Minkowski dans un référentiel tournant, bien que sa considération des vitesses superluminales soit excentrique par rapport à la pratique minkowskienne. Son étude est la seule des trois qui applique le formalisme minkowskien, et la seule à aboutir à une expression exacte de la géométrie spatio-temporelle du disque tournant.

5 Épilogue

Malgré les différences dans les points de départ, les trois cas présentés ici participaient tous dans le programme d’extension du principe de relativité. Pour Einstein, l’un des buts de ce programme était de pouvoir considérer “la rotation [comme] au repos”. Le travail de Kaluza semble avoir fait du progrès dans ce sens, mais il laissa entier le problème dynamique du disque tournant. C’était à ce problème dynamique qu’Einstein s’intéressait.

Einstein croyait que la théorie de la relativité généralisée et de la gravitation qu’il publia en 1913 avec le mathématicien zurichois Marcel Grossmann lui permettait d’obtenir des force centrifuges à partir du champ métrique d’un référentiel tournant (avec les conventions de mesure de la relativité restreinte). Plus tard, Einstein se rendit compte qu’il ne s’agissait pas d’une conséquence des équations du champ, mais on sait qu’il avait raison de croire que les phénomènes de gravitation–comme les forces centrifuges–sont des effets métriques, qu’il faut comprendre par rapport à la courbure de l’espace-temps par la matière.

À la place de l’espace-temps de Minkowski, Einstein et Grossmann mirent un espace-temps riemannien, où les intervalles indiqués par des barres et les horloges standardisées dépendent aussi bien de la distribution de la matière que du mouvement de l’observateur. Certes, l’emploi en physique d’un espace-temps riemannien en 1913 ne représente plus une grande nouveauté, comme nous l’avons vu par rapport au travail de Kaluza. D’ailleurs, la nécessité d’une métrique riemannienne pour sa théorie de la gravitation, remarqua Einstein plus tard, était indiquée par la géométrie du disque tournant (Stachel 1989, 55-56). En revanche, le fait de relier la courbure de l’espace-temps à la distribution de la matière, et l’emploi du calcul absolu de Ricci et Levi-Cività sont des innovations considérables.

Pendant les années 1910, Kaluza maintenait son intérêt à la relativité, et en 1921 publia une théorie d’unification des forces électromagnétiques et gravitationnelles en cinq dimensions, appelée aujourd’hui la théorie de Kaluza-Klein (Kaluza 1921, 966). Il semble même avoir suivi une démarche similaire à celle de sa théorie du disque tournant. Cette ressemblance méthodologique concerne la décomposition spatio-temporelle de la métrique du disque tournant, et celle de la théorie d’unification : dans celle-ci, la métrique à cinq dimensions est composée d’une métrique de l’espace-temps à quatre dimensions, et un vecteur de potentiel électromagnétique à quatre dimensions. Kaluza envoya son manuscrit à Einstein, qui lui fit part, en réponse, de son admiration pour “l’unité formelle” de la théorie.

Remerciements

Cet article reprend en partie un chapitre de notre thèse (Université Paris 7–Denis Diderot), rédigée avec le soutien d’une allocation de recherche (MESR). Sa forme a pu évoluer grâce aux commentaires et aux suggestions de plusieurs chercheurs, qui en sont vivement remerciés : Olivier Darrigol, Christian Houzel, Arthur Miller, Michel Paty, David Rowe et Andrew Warwick.

Notes

• ¹ Sur l’électrodynamique relativiste de Poincaré voir Cuvaj 1968 ; Darrigol 1994 ; Miller 1973 et 1981. Pour des comparaisons des contributions relativistes de Minkowski et d’Einstein voir Holton 1964, Galison 1979, Pyenson 1985, Walter 1999.
• ² Le formalisme quadridimensionnel est exposé dans Sommerfeld 1910a, 1910b ; Laue 1911b.
• ³ Notre critère d’inclusion est sémantique, et touche tout article portant mention de la relativité, de la cinématique d’Einstein, ou des transformations de Lorentz, ainsi que les variants comme, par exemple, les “transformations de Poincaré,” lorsque la référence à la relativité est évidente. Pour les détails de l’étude bibliométrique voir notre thèse (Paris 7, 1996), chapitre 4.
• ⁴ Voir, par exemple, Ehrenfest 1907, 204 ; Einstein 1907, 206 ; Sommerfeld 1907, 841.
• ⁵ Physikalische Zeitschrift 7, 1906, 761.
• ⁶ Voir les notes de Fritz Noether, dans le quatrième volume du texte de Klein et Sommerfeld, Über die Theorie des Kreisels (Klein et al. 1910, 939ff.) ; Frank & Rothe 1910, 616 ; Study 1914, ix, 108 ; Klein 1926, Vol. 2, p. 28.
• ⁷ Sur la carrière de Born, voir Richard Staley, "Max Born and the German physics community: the education of a physicist," unpublished Ph.D. dissertation, Cambridge University, 1992.
• ⁸ Born à Ehrenfest, 05.07.09, d’après Staley, op. cit., 153.
• ⁹ Born 1909a ; 1909b ; 1910, 233. Sur le mouvement rigide de Born dans la relativité restreinte et générale, voir Earman 1989.
• ¹⁰ Ehrenfest 1909, 918. Selon Born, l’impossibilité de mettre un corps rigide en rotation a été abordée par Einstein et Sommerfeld lors de la réunion de l’Association allemande à Salzburg. Einstein fit part de son intérêt dans le problème de rotation dans une lettre à Sommerfeld du 29.09.09, et nota une relation avec son étude des référentiels en mouvement rectiligne accéléré, publiée dans le Jahrbuch der Radioaktivität (Einstein 1993, Doc. 179; Stachel 1989). Pais (1982, 216) remarque dans le travail de Born un certain caractère riemannien ; la suggestion selon laquelle Einstein y trouva de l’inspiration pour la métrique non euclidienne de sa théorie de la gravitation est développée par Maltese et Orlando (1995).
• ¹¹ Cette contradiction a été appelée un paradoxe par Varicak (1911).
• ¹² Herglotz 1910 ; Noether 1910, 932. Quand la note d’Ehrenfest a été publiée, Herglotz expliqua aux lecteurs du Physikalische Zeitschrift que même s’il ne connaissait pas l’argument d’Ehrenfest lorsqu’il soumettait son travail sur le mouvement rigide de Born aux Annalen der Physik, ses résultats étaient compatibles avec la conclusion d’Ehrenfest (Herglotz 1909, 997). Herglotz et Ehrenfest se sont liés d’amitié pendant leur jeunesse à Vienne, où ils avaient suivi les cours de Boltzmann (Klein 1970, 36; Pyenson 1985, 106).
• ¹³ Sur les travaux de Donaldson et Stead voir Miller (1981, 269) et Warwick 1993.
• ¹⁴ M. Klein 1970, 153-4 ; Einstein 1993, 251 ; von Ignatowsky 1910, 630.
• ¹⁵ Donaldson et Stead 1911, 319-20.
• ¹⁶ Donaldson et Stead 1911, 324.
• ¹⁷ Nicholson 1912. Classé 12${}^{ème}$ Wrangler dans les Mathematical Tripos de 1904, Nicholson enseigna au laboratoire Cavendish avant d’être nommé en 1911 à une chaire de mathématiques à l’Université de Londres (Wilson 1956).
• ¹⁸ Stachel 1989.
• ¹⁹ La géométrie propre de Kaluza ne s’applique pas en général sur le disque tournant, parce qu’aucune série d’hypersurfaces successives n’existe pour laquelle les lignes d’Univers soient orthogonales.
• ²⁰ Max von Laue (1921, vol. 2, 163) déduisit cette métrique de la façon suivante. Prenons un système $S^{\prime}$ tournant avec une vitesse $\omega$ par rapport au référentiel au repos S, et deux points voisins en coordonnées polaires ($r$, $\varphi$) et ($r$, $\varphi$ + $d\varphi$). Pour mesurer la distance entre ces points, un observateur dans $S^{\prime}$ se sert d’une barre rigide de longueur $rd\varphi$ dans S ; sa vitesse est $v=r\omega$ par rapport à S. Pourvu que la transformation de Lorentz reste valable en $S^{\prime}$, la longueur de la barre $y$ est réduite par ($1-r^{2}\omega^{2}/c^{2})^{-1/2}$, où c signifie la vitesse de propagation de la lumière in vacuo (Kaluza mit $\omega$ et c égales à 1). L’observateur dans $S^{\prime}$ trouve donc que les deux points sont séparés par une distance $rd\varphi(1-r^{2}\omega^{2}/c^{2})^{-1/2}$. La métrique spatiale s’écrit alors selon la loi de Pythagore : $d\ell^{2}=dr^{2}+r^{2}d\varphi^{2}(1-r^{2}\omega^{2}/c^{2})^{-1/2}$. Du point de vue purement cinématique, la vitesse des éléments tangents à la rotation dépasse celle de la lumière lorsque $r\omega>1$ ; l’ambiguïté de signe se résout dès qu’on précise la longueur du rayon et la vitesse de rotation.
• ²¹ Dans le domaine réel ($r\omega<c$), la métrique spatiale de Kaluza correspond à une géométrie hyperbolique dans laquelle la courbure varie avec la distance de l’origine des coordonnées. On voit aisément que le rapport de la circonférence au rayon est plus grand que $2\pi$.
• ²² L’ambiguïté de signe disparaît lorsqu’on choisit r et $\omega$. Kaluza ne révèle pas comment il obtint cette expression ; pour la dérivation d’une formule équivalente, voir Arzeliès 1955, §102. Après la réintroduction des constantes, l’expression des géodésiques a la forme $\varphi-\varphi_{0}=\arccos r_{0}/r\pm r_{0}\omega^{2}/c^{2}(r^{2}-r_{0}^{2})^{-1/2}$.
• ²³ L’analogie emploie la substitution $\Psi=\arccos r_{0}/r$, tel que $R\sin\Psi=\pm R/r(r^{2}-r_{0}^{2})^{-1/2}$, et $R=rr_{0}$.
• ²⁴ Albert A. Michelson signala l’existence d’un effet optique de rotation du premier ordre en $v/c$ (appelé aujourd’hui l’effet Sagnac) en 1904, mais une erreur de calcul lui fit prévoir la moitié de l’effet de Kaluza. Une source probable de l’expérience de Kaluza est Fritz Noether, qui suggère en 1910 de revoir l’expérience de Michelson et Morley (1887) du point de vue de la rotation rigide. Paul Langevin (1935, 51) retrouva l’erreur de fermeture de Kaluza, ainsi que sa grandeur en cas de circumduction terrestre à l’équateur. Sur les applications récentes de l’effet, voir Soffel et Herold (1988).
• ²⁵ Le travail de Kaluza n’aurait pas plu au professeur de physique théorique à Königsberg Paul Volkmann, qui assimila la théorie de Minkowski à la métaphysique (1910, 149).
• ²⁶ Planck 1910 ; Ishiwara 1912, 644. L’intérêt physique du corps rigide de Born s’effaça davantage lorsque Max Laue montra que l’existence d’une vitesse maximale de propagation de signaux implique l’attribution d’un nombre infini de degrés de liberté au corps rigide lorsqu’on le met en mouvement (Laue 1911a, 85 ; Pauli 1958, 131). Les théoriciens se sont mis alors à l’étude de la théorie relativiste de l’élasticité ; voir von Ignatowsky 1911, et Herglotz 1911.
• ²⁷ Science Abstracts-Physics 1911, 78.
• ²⁸ Warwick 1993, 21.
• ²⁹ Un collègue de Nicholson à Birmingham, S. B. McLaren employait le formalisme minkowskien dès 1912 ; voir McLaren (1913).
• ³⁰ Einstein à Besso, 26.03.12, dans Einstein 1993, Doc. 377.
• ³¹ Selon Norton (1984, 142-3), quand Einstein reconnut que les équations du champ de la théorie de 1913 ne s’appliquent pas en cas de rotation uniforme, il reprit l’étude des équations de covariance générale. Sur la reconstruction du raisonnement d’Einstein, voir Janssen (à paraître).
• ³² Sur l’emploi de la géométrie non euclidienne en physique avant 1912, voir Walter 1998.
• ³³ Pais 1982, 330.

Bibliographie

Arzeliès, Henri. La cinématique relativiste (Paris : Gauthier-Villars, 1955).
Bonola, Roberto. Non-Euclidean Geometry, trad. H. S. Carslaw (New York : Dover Publications, 1955).
Born, Max. "Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips," Annalen der Physik 30 (1909a): 1-56.
—. "Über die Dynamik des Elektrons in der Kinematik des Relativitätsprinzips," Physikalische Zeitschrift 10 (1909b): 814-817.
—. "Über die Definition des starren Körpers in der Kinematik des Relativitätsprinzips," Physikalische Zeitschrift 11 (1910): 233-234.
Cayley, Arthur. "A sixth memoir upon quantics," Philosophical Transactions of the Royal Society of London 149 (1859): 61-90.
Cuvaj, Camillo. "Henri Poincaré’s mathematical contributions to relativity and the Poincaré stresses," American Journal of Physics 36 (1968): 1102-1113.
Darrigol, Olivier. "Henri Poincaré’s criticism of fin de siècle electrodynamics," Studies in History and Philosophy of Modern Physics 26B (1995): 1-44.
Dieks, Dennis. "Physics and geometry: the beginnings of relativity theory," in Kaczér, Jan (éd.), EPS-8: Trends in Physics (Prague : Czech Mathematicians and Physicists, 1991), pp. 969-982.
Donaldson, Harold et Stead, Gilbert. "The problem of uniform rotation treated on the principle of relativity," Philosophical Magazine 21 (1911): 319-324.
Earman, John. World Enough and Space-Time. Absolute vs. Relational Theories of Space and Time (Cambridge : MIT Press, 1989).
Ehrenfest, Paul. "Die Translation deformierbarer Elektronen und der Flächensatz," Annalen der Physik 23 (1907b): 204-206.
—. "Gleichförmige Rotation starrer Körper und Relativitätstheorie," Physikalische Zeitschrift 10 (1909): 918.
Einstein, Albert. "Zur Elektrodynamik bewegter Körper," Annalen der Physik 17 (1905): 891-921.
—. "Über die vom Relativitätsprinzip geforderte Trägheit der Energie," Annalen der Physik 23 (1907a): 371-384.
—. "Bemerkungen zu der Notiz von Paul Ehrenfest," Annalen der Physik 23 (1907b): 206-208.
—. "Relativitätsprinzip und die aus demselben gezogenen Folgerungen," Jahrbuch der Radioaktivität und Elektronik 4 (1907c): 411-462.
—. The Collected Papers of Albert Einstein, Vol. 5. The Swiss Years: Correspondence, 1902-1914 (Princeton : Princeton University Press, 1993).
Einstein, Albert et Grossmann, Marcel. Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation (Leipzig : Teubner, 1913).
Folkerts, Menso. "Kaluza, Theodor," in Neue Deutsche Biographie, Vol. 11 (Duncker & Humblot : Berlin, 1977): 76.
Frank, Philipp et Rothe, Hermann. "Über eine Verallgemeinerung des Relativitätsprinzips und die dazugehörige Mechanik," Sitzungsberichte der Kaiserlichen Akad. der Wiss. Wien IIA 119 (1910): 615-630.
Galison, Peter. "Minkowski’s spacetime: From visual thinking to the absolute world," Historical Studies in the Physical Sciences 10 (1979): 85-121.
Goenner, Hubert, Jürgen Renn, Jim Ritter and Tilman Sauer, eds. Einstein Studies Vol. 7 (Boston/Basel: Birkhäuser, 1999).
Hentschel, Klaus. Interpretationen und Fehlinterpretationen (Basel : Birkhäuser, 1990).
Herglotz, Gustav. "Bewegung ‘starrer’ Körper und Relativitätstheorie," Physikalische Zeitschrift 10 (1909): 997.
—. "Über den vom Standpunkt des Relativitätsprinzips aus als ’starr’ zu bezeichnenden Körper," Annalen der Physik 31 (1910): 393-415.
—. "Über die Mechanik des deformierbaren Körpers vom Standpunkt der Relativitätstheorie," Annalen der Physik 36 (1911): 493-533.
Holton, Gerald. "The metaphor of space-time events in science," Eranos Jahrbuch 34 (1965): 33-78.
Howard, Don et Stachel, John (éds). Einstein Studies, Volume 1 : Einstein and the History of General Relativity (Boston : Birkhäuser, 1989).
von Ignatowsky, Vladimir S. "Der starre Körper und das Relativitätsprinzip," Annalen der Physik 33 (1910): 607-630.
—. "Zur Elastitätstheorie vom Standpunkte des Relativitätsprinzips," Physikalische Zeitschrift 12 (1911): 164-169.
Ishiwara, Jun. "Bericht über die Relativitätstheorie," Jahrbuch der Radioaktivität und Elektronik 9 (1912): 560-648.
Janssen, Michel. "Rotation as the Nemesis of Einstein’s ‘Entwurf’ theory," in H. Goenner et al., 1999.
Kaluza, Theodor. "Zur Relativitätstheorie," Physikalische Zeitschrift 11 (1910): 977-8.
—. "Zum Unitätsproblem der Physik," Sitzungsberichte der königliche preußischen Akad. der Wiss. (1921): 966-972.
Klein, Felix. "Über die sogennante nichteuklidische Geometrie," Mathematische Annalen 4 (1871): 573-625.
—. Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert, 2 vols. (Berlin : Springer, 1926-1927).
Klein, Felix, Noether, Fritz et Sommerfeld, Arnold. Über die Theorie des Kreisels, Vol. 4 (Leipzig/Berlin : Teubner), 1910.
Klein, Martin J. Paul Ehrenfest: The Making of a Theoretical Physicist, Vol. 1 ( Dordrecht : North-Holland, 1970).
Langevin, Paul. "Remarques au sujet de la Note de M. Prunier," Comptes Rendus des séances de l’Académie des Sciences 200 (1935): 48-52.
von Laue, Max. "Zur Diskussion über den starren Körper in der Relativitätstheorie," Physikalische Zeitschrift 12 (1911a): 85-87.
—. Das Relativitätsprinzip (Braunschweig : Vieweg, 1911b).
—. Die Relativitätstheorie, 2 vols. (Braunschweig : Vieweg, 1921).
Laugwitz, Detlef. "Theodor Kaluza 1885-1954," Jahrbuch Überblicke Mathematik 19 (1986): 179-187.
Lecat, Maurice et Lecat-Pierlot, M. Bibliographie de la Relativité (Bruxelles : Lamertin, 1924).
Levi-Cività, Tullio. "Über Lorentz-Einsteinsche starre Bewegungen. (Auszug aus einem Briefe an Hrn. Prof. G. Herglotz)," Annalen der Physik 32 (1910): 236-240.
Maltese, Giulio et Orlando, Lucia. "The definition of rigidity in the special theory of relativity and the genesis of the general theory of relativity," Studies in the History and Philosophy of Modern Physics 26 (1995): 263-306.
McLaren, Samuel Brace. "Æther, matter and gravity," in Proceedings of the Fifth International Congress of Mathematicians, Vol. 2, sous la direction d’E. W. Hobson et A. E. H. Love (Cambridge : Cambridge University Press, 1913), 264-269.
Michelson, Albert A. "Relative motion of Earth and Aether," Philosophical Magazine 8 (1904): 716-719.
Michelson, Albert A. et Morley, Edward W. "On the relative motion of the Earth and the luminiferous Æther, Philosophical Magazine 24 (1887): 449-463.
Miller, Arthur I. "A study of Henri Poincaré’s ’Sur la dynamique de l’électron’," Archive for History of Exact Sciences 10 (1973): 207-328.
—. Albert Einstein’s Special Theory of Relativity: Emergence (1905) and Early Interpretation (Reading : Addison-Wesley, 1981).
Minkowski, Hermann. "Die Grundgleichungen für die electromagnetischen Vorgänge in bewegten Körpern," Nachrichten von der Kgl. Ges. d. Wiss. zu Göttingen (1908): 53-111; Mathematische Annalen 68 (1910): 472-525.
Nicholson, John William. "On uniform rotation, the principle of relativity, and the Michelson-Morley experiment," Philosophical Magazine 24 (1912): 820-827.
Norton, John D. "How Einstein found his field equations: 1912-1915," Historical Studies in the Physical Sciences 14 (1984): 253-316; in Howard et Stachel (1989): 101-159.
Pais, Abraham. ’Subtle is the Lord…’–the Science and the Life of Albert Einstein (Oxford: Oxford University Press, 1982).
Pauli Jr., Wolfgang. "Relativitätstheorie," Encyklopädie der mathematischen Wissenschaften 5 (1921): 539-775; trad. angl., Pauli (1958).
—. The Theory of Relativity (Oxford : Pergamon, 1958).
Planck, Max. "Gleichförmige Rotation und Lorentz-Kontraktion," Physikalische Zeitschrift 11 (1910): 294.
Poincaré, Henri. "Sur la dynamique de l’électron," Comptes Rendus des séances de l’Académie des Sciences 140 (1905); in Poincaré (1924), pp. 77-81.
—. "Sur la dynamique de l’électron," Rendiconti del Circolo Matematico di Palermo 21 (1906); Poincaré (1924), pp. 18-76.
—. La mécanique nouvelle (Paris : Gauthier-Villars, 1924).
Pyenson, Lewis. The Young Einstein: The Advent of Relativity (Bristol : Hilger, 1985).
Reich, Karin. Die Entwicklung des Tensorkalküls (Basel : Birkhäuser, 1994).
Soffel, M. et Herold, H. "Reference frames in relativistic space-time," in Babcock, Alice K. et Wilkins, George A. (éds.), The Earth’s Rotation and Reference Frames for Geodesy and Geodynamics (Dordrecht, 1988), pp. 99-103.
Sommerfeld, Arnold. "Ein Einwand gegen die Relativtheorie der Elektrodynamik und seine Beseitigung," Physikalische Zeitschrift 8 (1907): 841.
—. "Zur Relativitätstheorie. I. Vierdimensionale Vektoralgebra," Annalen der Physik 32 (1910a): 749-776.
—. "Zur Relativitätstheorie. II. Vierdimensionale Vektoranalysis," Annalen der Physik 33 (1910b): 649-689.
Stachel, John J. "The rigidly rotating disk as the "missing link" in the history of general relativity," in Howard & Stachel (1989), pp. 48-62.
Stead, Gilbert et Donaldson, Harold. "The problem of uniform rotation treated on the relativity principle," Philosophical Magazine 20 (1910): 92-95.
Study, Eduard. Die realistische Weltansicht und die Lehre vom Raume (Braunschweig : Vieweg, 1914).
Swann, William Francis Gray. "The problem of uniform rotation of a circular cylinder in its connexion with the principle of relativity," Philosophical Magazine 21 (1911): 342-348.
Volkmann, Paul. Erkenntnistheoretische Grundzüge der Naturwissenschaften (Leipzig & Berlin : Teubner, 1910).
Walter, Scott. "La vérité en géométrie : sur le rejet de la doctrine conventionnaliste, " Philosophia Scientiae 2 (1998): 103-135.
—. Minkowski, mathematicians, and the mathematical theory of relativity, in H. Goenner, J. Renn, J. Ritter, and T. Sauer (eds), The Expanding Worlds of General Relativity, Einstein Studies Vol. 7, Boston/Basel: Birkhäuser, 1999, 45–86.
Warwick, Andrew C. "Cambridge mathematics and Cavendish physics: Cunningham, Campbell and Einstein’s relativity 1905-11. Part II : Comparing traditions in Cambridge physics." Studies in History and Philosophy of Science 24 (1993): 1-25.
Wilson, William. "John William Nicholson." Biographical Memoirs of Fellows of the Royal Society 2 (1956): 209-214.