Poincaré on clocks in motion
Studies in History and Philosophy of Modern Physics
47(1), 2014, 131–141, doi:10.1016/j.shpsb.2014.01.003
Abstract:
Recently-discovered manuscripts throw new light on Poincaré’s discovery of the Lorentz group, and his ether-based interpretation of the Lorentz transformation. At first, Poincaré postulated longitudinal contraction of bodies in motion with respect to the ether, and ignored time deformation. In April, 1909, he acknowledged temporal deformation due to translation, obtaining thereby a theory of relativity more compatible with those of Einstein and Minkowski.
Contents
1 Introduction
In the month of May, 1905, Henri Poincaré (1905) was arguably the first scientist to express the principle of relativity in terms of the form-invariance of laws of physics with respect to transformations that form a particular group. This insight had several consequences for Poincaré’s understanding of what he called the “new mechanics” of relativity. Notably, following a method outlined by Lie and Scheffers (1893, 669), Poincaré identified invariants of the Lorentz transformation directly from the fact that the transformation is a rotation about the coordinate origin in four-dimensional space (with one imaginary axis). Any transformation of the Lorentz group, he noted further, may be decomposed into a dilation and a linear transformation leaving invariant the quadratic form , where light velocity is rationalized to unity. Poincaré naturally associated this quadratic form with the propagation of light, and gravitational action (Poincaré, 1906b, §§ 4, 8).
While historians agree that Poincaré discovered – and christened – the modern form of the Lorentz transformation, no consensus has formed on how Poincaré interpreted these same transformations in kinematic and dynamic settings. To some extent, the lack of consensus is a consequence of the state of the relevant textual sources, which are inconsistent at crucial junctures. The proximity of Einstein’s contributions to relativity and the theory’s rapid conceptual and formal evolution in its early years render the project of isolating the approach of either Poincaré or Einstein all the more difficult (Darrigol, 2004). In such a situation, there appears to be little prospect for the emergence of a common reading of Poincaré’s theory of relativity.
The situation has changed in the last year, as long-lost manuscripts have come to light which point the way to a new reading of Poincaré’s interpretation of the Lorentz group. This reading is presented here chronologically, beginning with a short history of local time, and an account of Poincaré’s lectures of 1906, in which he first considered the locus of light wavefronts in the context of Lorentz’s electron theory. Next, Poincaré’s adoption of a form of time deformation in 1909 is discussed, and is related to a reinterpretation of the Lorentz group employing clocks in motion. The final section takes up Poincaré’s mature presentation of the light-locus problem in lectures delivered in June, 1912. The paper closes with a discussion of Poincaré’s changing attitude toward the synchronization of clocks in motion, and situates his view in the context of spacetime conventionalism.
2 From Ortszeit to temps local
The theoretical foundations of classical electron dynamics were worked out by H.-A. Lorentz and Joseph Larmor beginning in 1895, and by 1900, electron theory was understood to represent the most sophisticated approach to a wide range of phenomena at the forefront of physics, from cathode rays and magneto-optics to blackbody radiation and the electrodynamics of moving bodies (Buchwald, 1985). After lecturing at the Sorbonne in 1899 on the theories of Lorentz and Larmor, Poincaré made a signal contribution to Lorentz’s electron theory, as Darrigol observes (1995). Lorentz’s theory explained the absence of measurable effects of uniform motion on electromagnetic phenomena to first order in (velocity over the vacuum speed of light), provided that one transformed the time variable according to spatial displacement and frame velocity to obtain :
| (1) |
or what Lorentz referred to as “Ortszeit” (Lorentz, 1895), and which Poincaré (1900a, 273), following Alfred Liénard, called “temps local”, or local time. In Poincaré’s mind, Lorentz’s local time took on an operational meaning, as the time read by a clock in uniform motion of velocity with respect to the ether, synchronized by crossed light signals with other identical comoving clocks, assuming isotropic propagation velocity. The difference between local time and “true” time for terrestrial clocks separated by one kilometer, according to Poincaré’s calculation, would be a third of a nanosecond, assuming an ether at rest with respect to the sun (Poincaré, 1901, 530).
In fact, Poincaré’s definition implies that measurement of the spatial separation of two clocks at relative rest is performed in the comoving frame, such that the local time transformation would be expressed as follows:
| (2) |
where . For terrestrial observers, the difference between (1) and (2) was insensible, which may explain its neglect.
First-order agreement with observed optical phenomena was unable to account for Michelson and Morley’s precise measurements of fringe shifts, which required the absence of terms up to third order in (Michelson and Morley, 1887). G.-F. FitzGerald and Lorentz suggested that a previously-unnoticed contraction of solids in the direction of their motion with respect to the ether would explain the null result of the Michelson-Morley ether-drag experiment, but it bothered Poincaré that independent hypotheses were required to explain the absence of first-order and second-order effects. He wondered aloud if the principle of relativity would not prove absolutely valid (Poincaré, 1900b, 1172).
At the same time, results obtained by a student of Gabriel Lippmann, Victor Crémieu, led Poincaré to doubt the validity of Maxwellian electrodynamics, or at least, the reality of the magnetic effect of electric convection. Lorentz and other theorists were convinced that if Rowland’s effect did not exist, this would spell ruin for both Maxwell’s theory and its successors, including Lorentz’s own electron theory. Crémieu’s attempt to reproduce the Rowland effect was unsuccessful, and in Poincaré’s considered opinion, the young experimenter had “rendered very doubtful a conclusion that seemed definitively established” (Poincaré, Rapport sur la thèse de V. Crémieu, 30.05.1901, in Walter et al., 2007, §2-62-6).
Poincaré’s confidence in Crémieu’s results stemmed in part from his conventionalist philosophy of science, which recognized the importance of observation and experiment in determining the direction of scientific research. Unlike his former student Pierre Duhem, Poincaré believed in the “crucial experiment”, the result of which determines the viability of theoretical options, or even of entire classes of theories. The investigations of the magnetic effect of charge convection performed by Crémieu, Pender and others provide an example of this type of experiment, inasmuch as a null result might have overturned the Maxwellian tenet of closed current loops, and with it, the electron theories of Larmor, Lorentz, and Max Abraham.
After a dramatic face-off in 1903 with Rowland’s student Harold Pender in Edmond Bouty’s laboratory at the Sorbonne, where the two experimenters labored in tandem to measure the Rowland effect, Crémieu recognized the effect’s reality, bringing the three-year controversy to a close (Walter et al., 2007, §2-17). It was an inglorious moment for Crémieu, and also for Poincaré, who since the early 1890s had been the leading exponent and expert on Maxwell’s theory in France (Darrigol, 1993).
Following the face-off, Poincaré silently rewrote the passage concerning the Rowland effect in the second edition of his popular collection of essays, La science et l’hypothèse:
Seemingly, the edifice of electrodynamics was definitively elaborated, at least in its principal aspects. This tranquil state of affairs was troubled recently by Mr. Crémieu’s experiments, which seemed for a moment to contradict the result obtained some time ago by Rowland. These experiments were disconfirmed by subsequent investigations, and Lorentz’s theory emerged victorious from the ordeal. (Poincaré, 1906a, 281)
In later editions of Poincaré’s book, the cited remark is nowhere to be found. But then Poincaré had no interest in reminding readers of Crémieu’s challenge to Maxwell-Lorentz theory, or of his own role in mounting and overcoming this challenge.
While Lorentz’s theory survived the charge-convection test, there would be others for it to pass. One of these tests was mentioned by Poincaré in September, 1904, a little more than a year after the resolution of the Crémieu-Pender controversy. Along with Gaston Darboux, Émile Picard, Paul Langevin and others, Poincaré was a member of the French delegation to the Congress of Arts and Science held during the World’s Fair in St. Louis. What threatened Lorentz’s theory in St. Louis was the notion of local time. Poincaré imagined the existence of non-luminous signals with hyperlight velocity, that we would use to verify the synchronization of light-synchronized timekeepers. Any difference in the result of the synchronization process would reveal the common motion of the clocks, in patent contradiction of the principle of relativity. The existence of such signals was not far-fetched, as Poincaré reminded his audience of Laplace’s calculation of the propagation velocity of gravitational action, which put the speed of gravitation at a million times that of light (Poincaré, 1904, 312).
Along with the Laplacian estimate of the velocity of gravitational action, the stability of the contractile electron appeared to menace Lorentz’s theory in 1904. An analysis of the hypotheses underlying electron theory led the Göttingen Privatdozent Max Abraham to point out that Lorentz’s theory was incomplete, insofar as it required a non-electromagnetic force for stability, and none had been proposed (McCormmach, 1970a, 51). With Abraham, a handful of theorists (including Paul Langevin, Alfred Bucherer, and Arnold Sommerfeld) were pursuing what Wilhelm Wien had called an “electromagnetische Weltbild”, or electromagnetic worldview, according to which, roughly stated, all physical interactions are of electromagnetic origin (McCormmach, 1970b). Abraham’s critique effectively excluded Lorentz’s theory from this attractive research program.
The exclusion of Lorentz’s electron theory from the electromagnetic worldview had no adverse effect on Poincaré’s view of the theory’s prospects, which he set out to improve in the spring of 1905. The motivation for Poincaré’s renewed interest in Lorentz’s theory is unknown, but may well be a consequence of his reading Lorentz’s recent papers on the topic, sent to him by Lorentz shortly before his visit to Paris at the end of April, 1905.11endnote: 1 Poincaré to Lorentz, ca. April 27, 1905 (Walter et al., 2007, §2-38-2). In addition to Lorentz’s papers, in the spring of 1905 Poincaré read Langevin’s theoretical study of electromagnetic inertia, where he developed formulas for velocity and acceleration waves issuing from an electron in motion.22endnote: 2 See (Langevin, 1905), referred to in (Poincaré, 1906b, 151).
Poincaré did not find the time to meet with Lorentz during the latter’s visit to Paris, but he did manage to perfect his electron theory. He announced his findings to Lorentz by letter soon after the latter left Paris. First of all, he corrected Lorentz’s current density transformation, such that charge is conserved. In doing so, he tried out three candidate transformations, corresponding to the electron models of Lorentz, Bucherer-Langevin, and Abraham. The latter model, in which an electron is likened to a rigid sphere, implied a property Poincaré was keen on preserving, but felt obliged to abandon:
You assume . Langevin assumes . I tried in order to preserve the unity of time, but this led me to inadmissible consequences.33endnote: 3 “Vous supposez . Langevin suppose . J’ai essayé pour conserver l’unité de temps, mais cela m’a conduit à des conséquences inadmissibles.” The symbols and were defined to be numerical constants: , where is the vacuum speed of light, and is frame velocity, while was defined by Lorentz to be a function of , for , differing from unity for small velocities by a second-order quantity at most (Lorentz, 1904, 813). (Poincaré to Lorentz, ca. May 1905, in Walter et al., eds., 2007, §2-38-3)
Abraham’s rigid-sphere electron theory preserved the unity of time, and required no non-electromagnetic forces for stability. But it was not compatible with the principle of relativity, and was discarded by Poincaré.
Lorentz’s reply to Poincaré has not been located, but after receiving it, Poincaré announced that his “ideas had changed”, and that he had come to a new understanding of the constant referred to in his previous letter. Rationalizing the velocity of light, Poincaré rewrote Lorentz’s transformation in a new, compact form:
and affirmed that this transformation forms a group if and only if . Where Lorentz had argued that on physical grounds, Poincaré expressed the principle of relativity in terms of group invariance: Lorentz’s transformation forms a group, and this transformation forms a group if and only if , therefore .
Not long afterwards, Einstein offered a derivation of what Poincaré called the “Lorentz transformations” from kinematic assumptions based on his twin postulates of relativity and light-speed invariance (Einstein, 1905, §3). To convince his readers of the compatibility of his postulates, Einstein showed that the equation of a spherical lightwave in one frame, say , has the same form when it is Lorentz-transformed. A spherical wave propagating with the speed of light in one frame, Einstein remarked, is thereby a spherical wave propagating with the speed of light in a second inertial frame. As the British mathematical physicist Ebenezer Cunningham pointed out later, form-invariance of the lightwave equation is all that is required for the derivation of the Lorentz transformation, along with a linearity constraint (Cunningham, 1907).
It is remarkable that Poincaré’s view of light propagation conflicted with that of Einstein and Cunningham, at least until 1909. Starting in the early 1970s, several commentators have noticed differences between Einstein’s and Poincaré’s views of light propagation, based on the latter’s diagrammatic model of the Lorentz transformation.44endnote: 4 See Cuvaj (1970, 74), Wright (1975, 453), Darrigol (1995; 2006; 2012), Damour (2005), Pierseaux (2005), and Rougé (2008). None of these contributions considers Poincaré’s view in its full chronological extent, i.e., from 1906 to 1912. To make matters more interesting, archival research turned up a long-lost manuscript, which throws new light on Poincaré’s model. The next section explores the latter source in detail.
3 Poincaré’s light ellipse and the limits of Newton’s laws (1906–07)
A few weeks after the above-mentioned exchange by mail with Lorentz, Poincaré communicated his results to the Paris Academy of Sciences (Poincaré, 1905). Following a trip to Scandinavia, and an audience with King Oscar II of Sweden, Poincaré finished a long memoir on the dynamics of the electron in July, 1905, which appeared in print the following January (Poincaré, 1906b). Curiously, for one who had engaged with the Riemann-Helmholtz-Lie problem of space, Poincaré avoided drawing consequences for the foundations of geometry from the “new mechanics” of the Lorentz group, with one exception. He observed that while previously, measurement of length implied the physical displacement of solids considered to be rigid,
this is no longer true in the current theory, if we admit the Lorentzian contraction. In this theory, two equal lengths, by definition, are two lengths spanned by light in the same lapse of time.
Light signals, in other words, constituted the new standard of both temporal and spatial measurement. But how was one to go about measuring lengths in a frame in motion, where measuring rods are Lorentz-contracted?
Poincaré’s measurement problem called for a solution, and after a while, Poincaré provided one. In lectures at the Sorbonne in 1906–1907, he interpreted the Lorentz transformation with respect to a geometric figure representing a meridional section of the wavefront of a light pulse, as judged by an observer at rest with respect to a luminous source in uniform motion. I will refer to Poincaré’s figure as a “light ellipse”. The light ellipse is a staple of Poincaré’s kinematics of relativity, in that he illustrated his view with this device on three occasions in public during the final six years of his life, from 1906 to July 12, 1912, and four times in print. A major change in Poincaré’s model of the Lorentz group took place in 1909, which will be the discussed in the next section.55endnote: 5 The three public presentations of the light ellipse are the following: (1) lectures at the Paris Faculty of Sciences, 1906–1907, student notes of which were edited by Marguerite Chopinet (1953), (2) a plenary lecture delivered at the annual meeting of the Association française pour l’avancement des sciences, published in two versions (Poincaré, 1909, 1910a), and (3) and lectures delivered at the École supérieure des postes et des télégraphes in Paris in June, 1912, published posthumously as (Poincaré, 1913). The light ellipse appeared first in print in a popular article on the dynamics of the electron (Poincaré, 1908a), reedited in the essay collection Science et méthode (Poincaré, 1908b).
From an historical standpoint, Poincaré’s view of the propagation of light from a source in uniform motion merits our attention for two reasons. His light ellipse was, first of all, a graphical illustration of kinematic relations in relativity theory, the first in a long line of techniques designed to display the relations of relativistic kinematics. Secondly, Poincaré’s model stands as the first of many attempts to reconcile an assumed Lorentz-covariance of physical laws with Galilean kinematics. These attempts have been largely neglected by historians, belonging as they do to a program that was increasingly marginalized by the success of Einstein-Minkowski relativity theory.66endnote: 6 For a notable exception, see (Chang, 1993).
While the inspiration for Poincaré’s light ellipse remains obscure, it may have been a response to Einstein’s derivation of the Lorentz transformation, mentioned above. A more likely source of inspiration is Langevin’s paper on electromagnetic inertia, also mentioned above, which features a discussion of the electromagnetic waves produced by an electron in motion with sublight velocity. Inventing such a diagram was not unusual for Poincaré, known for his skillful employment of diagrams to convey new ideas in mathematics and physics. Several of his figures gained notoriety over the years, including the disk and half-plane models of hyperbolic geometry, and the return map in systems dynamics.
The first known record of the light ellipse is found in notes taken by Henri Vergne, a student of Poincaré’s lectures in the 1906–1907 school year at the Paris Faculty of Sciences in the chair of Celestial Mechanics and Theoretical Astronomy.77endnote: 7 Henri Vergne (1879–1943) obtained his Ph.D. in mathematical sciences at the Paris Faculty of Sciences in 1909 (Vergne, 1909), and edited Poincaré’s 1910–1911 lectures on cosmogony for publication (Poincaré, 1911). Vergne later joined the faculty of the École Centrale in Paris, and served as president of the French Mathematical Society in 1939. Entitled “The limits of Newton’s laws”, these lectures were the first to present the principle of relativity in a university setting, but were not immediately edited. As Jean Chazy, a successor of Poincaré in the Chair of celestial mechanics, recounted the story in the preface to the publication, he asked Vergne if he could use the latter’s notes for his own lectures on the theory of relativity, and in response, Vergne made him a gift of the notes. Years later, Chazy sought to publish Vergne’s notes, and found in Marguerite Chopinet, astronomer at the Bordeaux Observatory, a willing editor. Chopinet’s edition of Vergne’s notes appeared in the Bulletin astronomique in 1953.
Chopinet’s edition of Vergne’s notebooks long served as the principal source for study of Poincaré’s 1906–1907 lessons. Until recently, it was the only source available, because the fate of Vergne’s notebooks was unknown. This was a particularly frustrating state of affairs, since Chazy had noted in his preface to Chopinet’s edition that the “mise au point” of Vergne’s notes was “delicate”. Comparison with Vergne’s recently-rediscovered notebooks reveals Chopinet’s numerous editorial additions, suppressions, and alterations, some of which are highly significant for historians of early-twentieth century physics and astronomy. A new, critical edition of Vergne’s notebooks is now forthcoming. In what follows, remarks on Poincaré’s 1906–1907 lectures refer only to Vergne’s notebooks.88endnote: 8 Vergne’s three notebooks were discovered in 2012 in the archives of the Bordeaux Observatory by Jérôme de la Noë, who arranged for their transfer to the Poincaré Archives.
In his Sorbonne lectures, Poincaré wanted to show that length and time measurements are transitive for inertial observers, transitivity being a sign of objectivity. To do so, he imagined a light source in uniform motion of velocity that passes through the coordinate origin at time . At a later time , the source reaches a point , such that the light-wave originating at time and propagating in all directions with speed has a spherical wavefront of radius . Figure 1, redrawn from Vergne’s notes, shows two light circles associated with three successive positions of the source: , , and . The larger light circle has center , and the smaller has center , as judged by an observer at rest with respect to the ether, with coordinate origin .
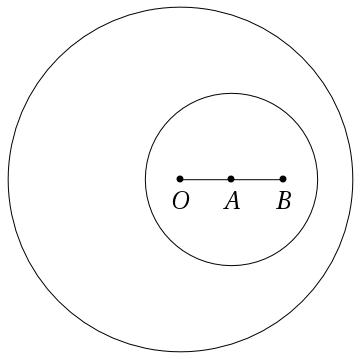
Poincaré then considered how a light sphere would appear if it were measured with rigid rods in uniform motion:
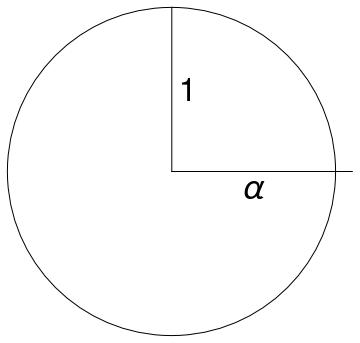
Now I take a rigorously spherical surface. I measure it with my meter stick, which will be contracted in the direction of motion by a factor , [such that] its true length will become . Therefore, my diameter in the direction of motion will have a measured length of . The measured length in the perpendicular direction will be 1. So a sphere will appear [as] an ellipsoid elongated in the direction of motion.99endnote: 9 “Alors je prends une surface rigoureusement sphérique. Je la mesure avec mon mètre: dans la direction du mouvement, mon mètre sera contracté de : sa longueur vraie sera devenue . Donc mon diamètre dans le sens du mouvement aura pour longueur mesurée . Dans le sens perpendiculaire la longueur mesurée sera 1. Donc une sphère paraîtra un ellipsoïde allongé dans le sens du mouvement.” The factor is defined to be , using modern notation. (Vergne, notebook 2, 49–50)
Vergne illustrated this measurement protocol with a diagram, featuring a circle with two line segments labeled “1” and “”, in the vertical and horizontal directions, respectively (Figure 2). [Note added on 2017-03-15: Figure 2 and the latter sentence have been modified to reflect the fact that in Vergne’s figure, is a line segment and not a radius.]
As it stands, Poincaré’s measurement protocol leaves us guessing about just who does the measuring, and this has led to some confusion.1010endnote: 10 For example, in Chopinet’s edition of Vergne’s diagram, the longitudinal radius is assigned length . Cuvaj, who referred to Chopinet’s edition, considered that measurement of the light shell was performed by comoving observers (Cuvaj, 1970, 74). It stands to reason, however, that Poincaré meant to measure a light shell with flying meter sticks, at a single instant of true time, as determined by a clock at rest with respect to the ether.1111endnote: 11 I agree here with Darrigol (2012). In order to demonstrate the transitivity of apparent time, Poincaré required ideal clocks at rest in the ether, rigid rods in motion, and light-point coincidences. The state of motion of the observer was incidental to the demonstration, in that the observer was assumed to be colocated with light-point coincidences. And while Vergne’s notes do not make explicit the latter assumption, they do employ the notion of a “point éclairé” or light point, and treat the distance between two such light points as null, or as an absolute invariant (Vergne, notebook 2, 51).
 |
Lorentz contraction | |
| Semimajor axis | ||
| Semiminor axis | ||
| Eccentricity | ||
| Focal length | ||
| Light path | ||
| Apparent displacement |
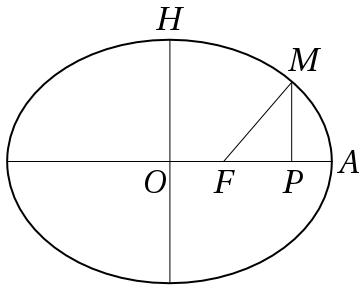
With these kinematic elements in place, Poincaré observed how the light path is related to apparent displacement. Poincaré’s argument proceeded as follows, based on the ellipse dimensions shown in Figure 3. From the diagram, Poincaré read off the standard relation for an ellipse with focus :
| (3) |
and then solved for :
| (4) |
the latter equation revealing the apparent time to be a linear function of apparent displacement , as desired.1212endnote: 12 Using the relations specified in Figure 3, we have Rearranging the latter expression in terms of , we find , and substituting the value of from (3) we obtain Poincaré’s expression (4) for apparent time, . The resemblance between (4) and (2) is remarkable, differing only by a factor . Poincaré seems not to have paid attention to this factor at first, but he did so in later years, as the next sections will show.
By simply rearranging (4), we obtain the transformation
| (5) |
and upon substitution for , we find in terms of :
| (6) |
The latter two equations appear in the same form (but with different notation) in Vergne’s notes, where their meaning is interpreted with respect to the light ellipse as follows:
Likewise, is the apparent time, since at two points the apparent time differs by a quantity proportional to the abscissa.1313endnote: 13 “De même est le temps apparent puisq’en 2 points le temps apparent diffère d’un quantité proport[ionnel] à l’abscisse.” (Vergne, notebook 2, p. 51)
The latter remark clearly refers to Poincaré’s equation (4). Consequently, the light ellipse was a means for Poincaré to convey not only the transitivity of time measurement in moving frames, but also the geometric and physical meaning of the Lorentz group.
Insofar as the light ellipse represented a locus of light for a single light pulse, it was ill-suited to represent the exchange of light signals between comoving observers. This was not an obstacle for Poincaré, who simply reversed the sign of the abscissæ difference:
I imagine that I’m realizing an exchange of signals: for the return [trip] from to :
Here we have
Therefore the difference is rigorously proportional to the abscissæ difference, without neglecting the square of aberration.1414endnote: 14 “Je suppose que je fasse l’échange des signaux: j’aurai p[ou]r le retour de en : (car l’abscisse a un signe). Ici . Donc la différence est rigoureusement proport[tionnel] à la différence des abscisses, et sans négliger le carré de l’abérration.” (Vergne, notebook 2, 50, original emphasis, and replaced by and )
Updating the notation, denoting the light time-of-flight from to by , and that from to by , and using (5), we can express the above expressions as:
Notice that Poincaré’s thought experiment involves observers in motion exchanging light signals, but does not involve clocks in motion, since light time-of-flight is measured in true time, , not apparent time, . Comoving observers have no access to true time, of course, which may be one reason why Poincaré never used this particular thought experiment again.
In summary, using a thought experiment, Poincaré compared the form of a light pulse for an observer at rest with respect to the ether, at a single instant of time in the ether frame, for two cases: (1) meter sticks at rest in the ether frame, and (2) meter sticks in uniform motion. He judged the form in the first case to be that of a sphere of radius , and in the second case, that of an ellipsoid of rotation, elongated in the direction of motion of the meter sticks, with semiminor axis of length , and semimajor axis of length . He associated the dimensions of the ellipsoid with the length and time variables of the Lorentz group, but did not interpret the light ellipse in terms of clocks in motion.

The foregoing reading of Poincaré’s light ellipse is passingly strange, in that it has Poincaré blithely mixing kinematic quantities from different inertial frames. Braving the risk of anachronism for a moment, let’s consider Poincaré’s thought experiment with a cognitive tool he did not dispose of: the three-dimensional Minkowski diagram. According to the interpretation of the Lorentz group in Vergne’s notes, the radius vector of the light ellipse corresponds to light points at an instant of time as read by clocks at rest in the ether frame. The representation of this situation on a Minkowski diagram is that of an ellipse contained in a spacelike plane of constant time (Figure 4). The ellipse center coincides with spacetime point , and the points , , , and lie on the major axis, such that is a semiminor axis of length . The light ellipse intersects the lightcone in two points, corresponding to the endpoints of the minor axis, and . There are no moving clocks in this reading, only measuring rods in motion with respect to the ether, and clocks at rest. (The -axis is suppressed in Figure 4 for clarity).
The abstract nature of Poincaré’s early interpretation of the Lorentz group is apparent in the Minkowskian representation, in that there are points on the light ellipse that lie outside the lightcone, these points representing locations in spacetime physically inaccessible to all inertial observers sharing a spacetime origin. In four-dimensional Minkowski spacetime, the intersection of the light sphere with center and the light ellipsoid with center , where and lie on a spacelike plane, is a circle of radius . On a three-dimensional Minkowski spacetime diagram, where one spatial dimension is suppressed, the corresponding circle with center and ellipse with center intersect in two points, labeled and , such that . The diagram shows that in Poincaré’s light-ellipse model of the Lorentz group, there are physical events bereft of any causal connection to observers that are nonetheless ascribed to these same observers.1515endnote: 15 In 1912, Poincaré singled out the set of events which can be neither the cause nor the effect of other given events, and attributed its discovery to the employment of a four-dimensional (3+1) vector space (Walter, 2009).
Minkowski diagrams were not at hand when Poincaré delivered his lectures at the Sorbonne, but other cognitive resources were available, which could be applied to Poincaré’s thought experiment. For example, for those who had been following the work of Einstein, there was the notion of time dilation. Yet this notion, too, is absent from Vergne’s notes. Instead of time dilation, what we find is a recapitulation of Poincaré’s operational (first-order) definition of local time, mentioned above, along with the following comment on Lorentz contraction and clock synchronization:
So Lorentz assumes that all bodies undergo a contraction in the direction of motion proportional to the square of velocity. Lengths are then altered, and durations are altered by the impossibility of setting watches truly, such that the apparent velocity of light is constant. Then we perform a Lorentz transformation: the Lorentz transformations must form a group, such that we have identically .1616endnote: 16 “Donc Lorentz suppose que tous les corps subissent dans la direction du mouvement une contraction proport. au carré de la vitesse. Alors les longueurs sont altérées, et les temps sont altérés par l’impossibilité de régler vraiment les montres, ce qui fait que la vitesse apparente de la lumière est constante. Alors nous effectuons une transformation de Lorentz : les transfor. de Lorentz doivent former un groupe, tel que l’on ait identiquement .” (Vergne, notebook 2, 52)
What Poincaré taught his students, in other words, was that clocks in motion cannot be set properly, and consequently, are unreliable timekeepers. This view of clocks in motion is consistent with his earlier operational definition of local time (mentioned above), according to which light-synchronized clocks in uniform motion are reliable only to first order in . It is also consistent with his light-ellipse interpretation of the Lorentz group, which puts meter sticks in motion to measure a light shell, but which does not put clocks in motion. Perhaps most compellingly, the strange blend of kinematic attributes from different frames of motion manifested in the Poincaré’s presentation of the light ellipse faithfully mirrors that of the terms in Poincaré’s formula for apparent time (4), where apparent time is the sum of true time and the product of velocity with apparent displacement, divided by the square of the speed of light. In the next section, I will show that Poincaré’s confidence in moving clocks increased over time, leading him to embrace time deformation.
4 Poincaré on time deformation
The light ellipse was known only to Poincaré and his students until he published an essay in the March, 1908 issue of Revue générale des sciences pures et appliquées. This essay recapitulated the presentation of the light ellipse found in Vergne’s notes, with one important exception. Where Vergne’s notes defined “apparent time” according to (4), and identified this time with the temporal variable appearing in the Lorentz transformation, in the Revue Poincaré called the quantity “apparent duration” (Darrigol, 2012, note 69). Despite this change in nomenclature, when discussing the light ellipse, Poincaré kept his clocks firmly planted in the ether, and his meter sticks flying by at constant velocity.
This change in nomenclature is linked to Poincaré’s growing appreciation of the fact that all inertial frames are physically equivalent, and that this equivalence extends to timekeepers. His discussion of the light ellipse in the Revue concluded with the following remark:
[I]t is impossible to escape the impression that the principle of relativity is a general law of nature, that we could never make manifest, by any means imaginable, anything other than relative motions, by which I mean not just velocities of bodies with respect to the ether, but velocities of bodies with respect to each other.1717endnote: 17 “[I]l est impossible d’échapper à cette impression que le principe de relativité est une loi générale de la Nature, qu’on ne pourra jamais par aucun moyen imaginable mettre en évidence que des vitesses relatives, et j’entends par là non pas seulement les vitesses des corps par rapport à l’éther, mais les vitesses des corps les uns par rapport aux autres.” (Poincaré, 1908a, 393)
One consequence of the equivalence of inertial frames – including the ether frame – is that if timekeepers can be synchronized in one frame, then they can be synchronized in every frame. Furthermore, if the ether is not to be distinguished by physical means from any other inertial frame, then mixing kinematic attributes from different frames, which is just what Poincaré did in the pages of the Revue, makes little sense. It is curious that Poincaré did not immediately revise his presentation of the light ellipse to reflect this understanding of the principle of relativity, but as I shall show in the next section, such a revision would soon be at hand.
The roots of Poincaré’s coming revision of the light ellipse are apparent in Poincaré’s change in nomenclature, an echo of which is to be found in his subsequent discussion of relative velocity. Poincaré’s approach to the question of relative velocity in the Revue is of particular interest. While he had previously disclosed the relativistic law of velocity addition, which he read off the infinitesimal generators of the Lorentz group (Poincaré, 1906b), he had not shown how to interpret this law operationally. The way to do this, Poincaré explained in a nutshell to the readers of the Revue, was to employ local time, instead of “true” time. The local time in question was not the first-order version Poincaré had advanced in 1900, but that of the modern Lorentz transformation, with a factor , as in (4). Furthermore, the evaluation of local time was not to be performed with flying rods and a light pulse, but with clocks in motion.
Poincaré imagined a pair of observers located at points and at relative rest, in motion with respect to a given frame , with velocity m/s, and a body with an equal velocity moving in the opposite direction, and passing successively through points and , such that the velocity difference of the observer pair and the body is m/s with respect to , well in excess of the speed of light. To judge the velocity of a body with respect to the pair of observers in the moving frame, Poincaré explained, it was necessary to refer to local time. The velocity of a body in motion relative to these observers was determined by
…noting the instant it passes through in the local time of , and the instant it passes through in the local time of , such that the trip duration will be , and the relative velocity: . And this is how the compensation happens.
Since the quantity in parentheses, , is equal to , it is just what Poincaré defined operationally as local time in 1900.1818endnote: 18 Poincaré denoted the true time at which the body reached point by , and the true time at which the body attained point by , such that the elapsed true time for the body’s displacement between points and is . By comparison with (4), , and since is the true elapsed time, , we have . Likewise, Poincaré denoted the times of passage of the body in terms of true time, . The time at which the body reaches point is for observer and for observer . The time at which the body reaches point is for observer , and for observer . Subtracting the time of the body’s passage through as marked by observer from the time of passage of the body through as marked by observer results in Poincaré’s value for trip duration from to , . Consequently, what Poincaré referred to here as the “trip duration” is just what he had called “apparent duration” in his discussion of the light ellipse a few pages earlier, or . The “compensation” mentioned by Poincaré refers to the difference in rate of the observers’ timekeepers, compared to that of timekeepers at rest in the ether, which mark “true” time.
Roughly a year later, Poincaré’s confidence in clocks in motion was on the rise. Much had happened in the previous year to motivate a new look at time deformation in relativity theory. Hermann Minkowski had proposed his theory of spacetime, based on the same four-dimensional vector space introduced by Poincaré. According to Minkowski’s theory, clocks in motion read “proper time”, defined to be the parameter of their worldline in spacetime (Minkowski, 1908). Einstein made a number of bold predictions concerning the behavior of atomic vibrations, including the manifestation of time dilation via a transverse Doppler effect in the spectrum of canal rays (Einstein, 1907b), and the redshift of spectral lines in a gravitational field (Einstein, 1907a).
The occasion Poincaré chose for a stronger embrace of time deformation was a significant one for Franco-German relations. In the fall of 1908, the mathematician David Hilbert invited Poincaré to deliver a series of lectures in Göttingen, sponsored by the Wolfskehl Foundation. Poincaré did not plan at first to speak about relativity, a field scientists in Göttingen followed closely, following their colleague Minkowski’s signal contributions. Minkowski and Hilbert were great friends, and the former’s sudden death in January, 1909, grieved Hilbert deeply, as the latter shared in a letter to Poincaré a few weeks after the sad event. Hilbert then asked Poincaré to consider supplementing the lectures he had scheduled for “Poincaré-week” with a talk on mathematical physics or astronomy. In response to Hilbert’s request, Poincaré delivered a talk in French on the “new mechanics”, which took up the theory of relativity and its consequences for astronomy.1919endnote: 19 Hilbert to Poincaré, 25 February, 1909, henripoincarepapers.univ-nantes.fr/chp/text/hilbert-1909-02-25.html. On research traditions in mathematics and mathematical physics in Göttingen at the turn of the twentieth century, see Rowe (1992) and Corry (2004).
On the opening day of Poincaré-week, Hilbert and his wife Käthe entertained Poincaré at their home in Göttingen, in the presence of Felix Klein and other guests. Klein turned sixty that day, and Hilbert jumped on the occasion to honor his colleague, and to pun upon a singular achievement of his recently-lost friend:
Your little ship is still moving ahead with youthful vigor at a full clip. Minkowski taught us that the concept of simultaneity (Gleichzeitigkeit) is relative. This applies even more so to the concept of age (Gleichaltrigkeit). (Cited by Rowe, 1986)
Hilbert’s joke about relative simultaneity had an edge to it, in that unlike Minkowski, Poincaré had not yet adopted the notion of frame-dependent time.
Three days later, in the course of his sixth and final Wolfskehl lecture, on 28 April, 1909, Poincaré returned to the topic of relative velocity that he had discussed in the pages of the Revue générale des sciences pures et appliquées, as mentioned above. This time, however, he introduced two observers and in relative motion, equipped not just with timekeepers, but with wireless transmitters and receivers. As a member of the French Bureau of Longitudes, and a leading expert on wireless telegraphy, Poincaré naturally equipped his observers with the means of transmitting time-stamped position data on the fly.2020endnote: 20 For a review of Poincaré’s activity at the Bureau of Longitudes, see Galison (2003), and for discussion of his engagement with contemporary technological issues, including wireless telegraphy, see Gray (2013, 177).
In spite of all this equipment, comoving observers were still unable to detect their absolute motion:
can believe he is at rest, and ’s apparent speed will be 400000 km/s. If knows the new mechanics he will say to himself: “ has a speed that he cannot attain, so it must be that I, too, am in motion.” It seems that he could determine his absolute situation. But he would have to be able to observe ’s motion. To make this observation, and begin by setting their watches, then sends telegrams to indicating his successive positions; putting these signals together, can give an account of ’s motion, and trace its curve. Well, the signals propagate at the speed of light; the watches marking apparent time vary at every instant and it all will go down as if ’s watch were fast.2121endnote: 21 “ peut se croire au repos et la vitesse apparente de sera, pour lui, 400000 kilomètres. Si connaît la mécanique nouvelle il se dira: a une vitesse qu’il ne peut atteindre, c’est donc que moi aussi je suis en mouvement. Il semble qu’il pourrait décider de sa situation absolue. Mais il faudrait qu’il puisse observer le mouvement de lui-même; pour faire cette observation et commencent par régler leurs montres, puis envoie à des télégrammes pour lui indiquer ses positions successives; en les réunissant, peut se rendre compte du mouvement de et tracer la courbe de ce mouvement. Or les signaux se propagent avec la vitesse de la lumière; les montres qui marquent le temps apparent varient à chaque instant et tout se passera comme si la montre de avançait.” (Poincaré, 1910b, 54–55)
The tabulation of telemetric data would, in principle if not yet in practice, suffice to show that the watches of the two observers in relative motion did not run at the same rate. This is the first time that Poincaré explicitly invoked the deformation of time due to translation, although as shown above, a year earlier he employed the notion in his algebraic analysis of relative motion for the Revue générale des sciences pures et appliquées.
The concept of time deformation employed by Poincaré in Göttingen and thereafter was quite distinct from that of Einstein and Minkowski. For the latter theorists, time dilation and length contraction were kinematic effects, or consequences of the four-dimensional (3+1) metric of spacetime, respectively. According to Poincaré, the velocity dependence of measured lengths and durations was best understood as a result of compensating deformations of meter sticks and timekeepers. In the wake of Minkowski spacetime, the absolute space and time of Newtonian mechanics took on a conventional nature for Poincaré, for whom the concept of Galilei spacetime had not lived out its utility for science, and would not do so for some time (Poincaré, 1912).
Henceforth for Poincaré, clocks could be put in motion and used to indicate the time of events for comoving observers. The rate of clocks in motion exceeds that of clocks at rest with respect to the ether by just the amount required by the principle of relativity. This was a significant step for Poincaré, and one that led him to adjust his account of the light ellipse. It also brought his theory into an apparent conflict with those of Einstein and Minkowski, where clocks in motion run slower than those at rest. This difference was linked to Poincaré’s reading of the light ellipse, as I will show in the next section.
Three months after Poincaré-week in Göttingen, Poincaré had another opportunity to speak to the topic of the new mechanics. He was invited to deliver the opening lecture of the Congress of the French Association for the Advancement of Sciences held in Lille, on the third of August, 1909, and used the occasion to rehearse his analysis of relative motion, and to explain how the light ellipse captures the behavior of clocks in motion.
In Lille, Poincaré once again considered the form of a light pulse for a source in uniform motion, and modeled light paths with the radius vector of an ellipse elongated in the direction of motion. Denoting the head and tail of the radius vector by and , respectively, Poincaré explained that clocks in motion could not reveal the motion to comoving observers:
Now let’s suppose that an observer is comoving with the luminous body. […] To this observer, wave surfaces would appear to be elongated in the direction of motion; they will appear to him to be ellipsoidal. All these ellipsoids will be mutually homothetic, and the luminous body will occupy a focus.
Under these conditions, a very elementary geometrical theorem shows that the apparent time required for light to travel from to , i.e., the difference between the local time at when the wave leaves and the local time at when the wave reaches , this apparent time, I say, is the same as if the translational motion did not exist, just as required by the principle of relativity.2222endnote: 22 “Supposons maintenant un observateur entraîné dans la même translation que le corps lumineux. […] Des surfaces d’onde sembleront donc à notre observateur allongées dans le sens du mouvement; elles lui paraîtront ellipsoïdales. Tous ces ellipsoïdes seront homothétiques entre eux, et le corps lumineux en occupera un foyer.
Dans ces conditions, un théorème de géométrie très simple montre que le temps apparent que la lumière mettra à aller de en , c’est-à-dire la différence entre le temps local en au moment du départ de , et le temps local en au moment de l’arrivée en , que ce temps apparent, dis-je, est le même que si la translation n’existait pas, ce qui est bien conforme au principe de relativité.” (Poincaré, 1909, 173–174, original emphasis)
Unlike earlier presentations of the light ellipse, the Lille version features comoving observers and clocks. These comoving observers record both the emission time of the light pulse at the focal point , and the time of detection of the pulse at a point . The “geometrical theorem” referred to here is the same as the one noted by Vergne, expressed in (3). Both the radius vector of the light ellipse and the radius of a light circle are supposed by Poincaré to represent light paths. But what remains unclear in Poincaré’s presentation is how the radius vector, the length of which varies with the angle formed with the ellipse axes, models the radius of a corresponding light circle. The details of this model were disclosed by Poincaré three years later (see below, section 5).
What led Poincaré to replace his flying rods and observers at rest in the ether by comoving observers and clocks? He never explained this remarkable revision of his light ellipse. My guess is that the lightcone structure of spacetime discovered by Minkowski led Poincaré to realize that his earlier presentation of the light ellipse was untenable, and that by replacing ether-fixed observers by comoving observers, he could obtain a satisfactory model of light propagation.
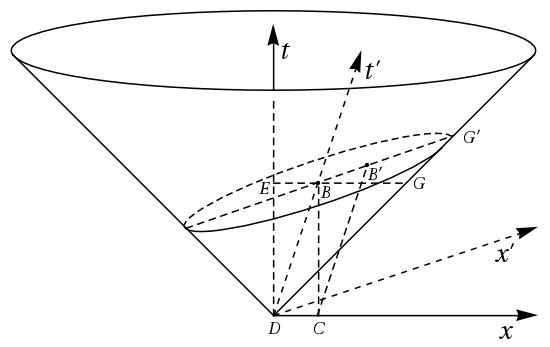
According to Poincaré’s revision in Lille of the light ellipse, the light pulse is measured with comoving clocks and meter sticks, such that the corresponding figure on a three-dimensional spacetime diagram is an ellipse in a plane of constant time, . The latter -plane intersects the lightcone at an oblique angle, as shown in Figure 5, such that their intersection is a Poincaré light ellipse. (The -axis and the -axis are suppressed for clarity). By adopting comoving clocks and observers, Poincaré successfully transformed his light ellipse from a physically-untenable interpretation of the Lorentz group to a relativistic interpretation of time dilation and Lorentz contraction. In the next section, I examine Poincaré’s most detailed, and final presentation of the subject of time deformation and the light ellipse.
5 The light ellipse at the École des postes and télégraphes
In the month of June, 1912, Poincaré delivered a series of lectures for the benefit of students of electrotechnology at an engineering school in Paris overseen by the Ministry of the Post and Telegraph, the École supérieure des postes et des télégraphes, or “ESPT” for short. Poincaré, who was engaged by the ESPT as Professor of theoretical electricity in 1902, delivered courses on advanced topics in electrical engineering, which were usually transcribed by student note-takers for publication in the biweekly Éclairage électrique, or its successor, Lumière électrique, the editorial board of which he was a member. Like the topics of earlier lecture series, that of 1912 was suggested by the Ministry of the Post and Telegraph, which financed and managed the ESPT (Guillet, 1988). Poincaré acknowledged that his topic differed from those of previous years, which saw him cover questions directly relevant to “engineering arts”, such as current propagation, telephony, and wireless telegraphy. Apparently, the Ministry had exhausted its stock of engineering topics ready-made for the application of principles of mathematical physics, and was consequently “forced to exit the circle” of such topics, in order to find one suited to Poincaré’s theoretical bent. The topic assigned for the 1912 series was thus chosen to be the dynamics of the electron, said Poincaré, adding that he would also examine the principle of relativity. He expressed the hope that telegraphists, in spite of the absence of any immediate practical application of the theory of electron dynamics, would nonetheless find his remarks to be of interest, inasmuch as they represented “modern ideas relative to the theory of electricity” (Poincaré, 1913, 18).
The lectures delivered by Poincaré at the ESPT are among the last that he would have the chance to deliver, and he passed away before he had the opportunity to review the notes transcribed by Jean-Baptiste Pomey, one of Poincaré’s fellow professors. In what follows, I focus on just two of the many topics treated in detail by Poincaré: time deformation and the light ellipse.
Poincaré began his discussion of time deformation by recalling his operational definition of local time, which guaranteed the relativity of optics to the first order of approximation. Denoting apparent time by and “real” time by , Poincaré rewrote the expression for apparent time: , where is a constant depending on position (in Poincaré’s original formulation, ). He continued:
But this is insufficient, and we have to suppose further that
(7) By introducing the coefficient , we admit that mechanical phenomena are accelerated by a motion of translation. The constants and will depend on , and will continue to depend on the position of the point. This accounts for the compensation, at least in optics.2323endnote: 23 “Mais ceci n’est pas suffisant, il faut encore supposer que l’on a: . L’introduction du coefficient revient à admettre que les phénomènes mécaniques sont accélérés par un mouvement de translation. Les constantes et dépendront de , et continue à dépendre de la position du point. Ceci rend compte de la compensation tout au moins en optique.” (Poincaré, 1913, 44)
The acceleration of mechanical phenomena referred to here undoubtedly included those of mechanical timekeepers, which would explain the remark cited earlier about watches in motion marking apparent time, where the watches were given to be running “fast” with respect to a watch at rest. According to (7), timekeepers run fast or slow depending on the value of . From what follows in the notes of Poincaré’s ESPT lecture, it appears that Poincaré associated not with , as in (6), but with , as in (4). Consequently for Poincaré, timekeepers in motion run faster, not slower, than timekeepers at rest. Had he associated (7) with (6), he would certainly have come to the conclusion that timekeepers in motion run slower than timekeepers at rest, in agreement with Einstein and Minkowski.
While the mathematical form of time deformation is the same here as that employed in Poincaré’s discussion of relative motion in the Revue générale des sciences pures et appliquées, four years earlier (letting , see note 18), a more transparent expression of the basis for time deformation is not to be found in Poincaré’s writings.
Following this review of the basis of time deformation, Poincaré turned to the light ellipse. As mentioned in the previous section, Poincaré argued without proof in Lille that comoving observers could not detect their absolute motion with comoving clocks and meter sticks. Three years later, he finally provided a proof of sorts, by showing that the light ellipse is an isochronous figure.

The proof that the light ellipse is an isochronous figure proceeded much in the same way as in his previous discussions of the light ellipse, by characterizing the difference between two observer stations located on the ellipse, one of which coincided with a focus . This time around, however, Poincaré introduced a directrix and a point such that is orthogonal to the major axis (Figure 6).
The light ellipsoid (for which the ellipse is a meridional section) corresponded now as ever to a real light sphere of radius . In the “ideal” space of comoving observers, Poincaré explained, the apparent time depends on true time, , such that:
| (8) |
where denotes the semiminor axis length, and the term is a function of the difference of abscissæ of the ellipse point and the focal point . Consequently, we can write, using slightly-modified notation:
| (9) |
where is an unknown constant. Since is equal to the semilatus rectum , is related to by the eccentricity, :
| (10) |
With these elements in place, Poincaré announced his objective (letting ):
We want the apparent time to be the same as if [the observer] were at rest; in other words, we want to have .2424endnote: 24 “Nous voulons que le temps apparent soit le même que si l’on était au repos, c’est-à-dire que l’on ait : .” (Poincaré, 1913, 46)
What Poincaré wanted to show his audience, was that the apparent time is measured by the radius vector of the ellipse, , just as the true time is measured by the radius of the corresponding light circle, . True time was measured against the ordinate of the light ellipse, just as apparent displacement was measured against the abscissa. A quick calculation shows that a judicious choice of the parameter preserves the principle of relativity, as Poincaré wished.2525endnote: 25 From (9) and , we can write: and by inspection of Figure 6: Letting , we obtain: (11) Recalling the identity , along with (11), we find: (12) The published notes of Poincaré’s lectures at the ESPT do not develop the argument beyond (12), but if we recall the values of the parameters (reintroducing ): , , and , we find the transformation: Recalling that , and , the latter equation is seen to be equivalent to (4), which can be rearranged to give the modern Lorentz transformation (6), as shown above.
In harmony with Poincaré’s presentation of the light ellipse in Lille, his lesson on the light ellipse at the École supérieure des Postes et des Télégraphes in Paris, three years later, featured comoving observers who employ comoving clocks and Lorentz-contracted meter sticks to discover the form of the light pulse emitted by a comoving source. Poincaré showed that the comoving observers are unable in principle to detect their motion, filling a gap left in his presentation in Lille, and in full agreement with the principle of relativity.
6 Discussion
Historical and philosophical analyses of the discovery and early development of the theory of relativity have shown that the scientific community did not welcome the relativity revolution, but required a great deal of convincing before it abandoned the competing worldviews.2626endnote: 26 For an overview, see Staley (2008). The energetic and vocal promotion of Einstein’s theory on the part of Max Planck and others brought it significant attention, but many questions remained concerning the theory’s logical and mathematical cogency, empirical validity, and potential utility in theoretical and experimental realms. In 1908, Minkowski’s theory of spacetime resolved several of the quandaries of the first sort, while the results of Bucherer’s electron-deflection measurements did much to establish the empirical credentials of relativity theory. Poincaré’s review in March, 1908, of the outlook for the principle of relativity participated in this movement, by affirming the general validity of the principle of relativity for all inertial frames.
Poincaré’s message, however, was quite different from that of Einstein or Minkowski. While Poincaré presented the first geometric interpretation of the Lorentz group, the image he presented – that of a light ellipse – was mathematically impeccable, but flawed from a physical standpoint. The next year, in 1909, Poincaré invoked the notion of translation-induced time deformation, and introduced comoving observers and clocks to his light-ellipse interpretation of the Lorentz group. His reasons for doing so are open to speculation, but my guess is that, like so many other theorists in physics and mathematics, Poincaré was impressed by Minkowski’s spacetime theory, where the time read by clocks is a path-dependent quantity. In any case, once Poincaré had revised his presentation of the light ellipse so that it featured comoving clocks, meter sticks and observers, the ellipse could be represented in a spacetime diagram as an oblique section of a three-dimensional light cone, thereby bringing his own theory of relativity closer to that of Minkowski.
An important distinction remained between the theoretical views of Poincaré, Einstein and Minkowski, despite Poincaré’s embrace of clocks in motion. As far as Einstein and Minkowski were concerned, if a light wave was spherical in one inertial frame, it was spherical in all such frames. Not so for Poincaré, who held that, because of Lorentz-contraction of solids in the direction of motion, comoving observers would necessarily conclude that a light shell measured as a sphere was in fact an ellipsoid of rotation, elongated in the direction of motion. This fact was of no use to comoving observers in objectively determining their state of motion, and it appears to have misled Poincaré into believing that clocks in motion run faster than clocks at rest.
None of Poincaré’s contemporaries appears to have employed, or even commented upon the light ellipse, and in this sense, it is safe to say that the diagram was a faithful expression of Poincaré’s understanding of the Lorentz group. The light ellipse was a valuable pedagogical device for Poincaré, since he rarely missed an occasion to employ it. The radical revision of his presentation of the light ellipse in 1909, replacing observers and clocks at rest in the ether by comoving clocks, meter sticks and observers, brought his theory into compliance with the Einstein-Minkowski interpretation of the Lorentz group. At the same time, it suggested that one could adopt the principle of relativity without sacrificing Galilei spacetime. Poincaré convinced himself that such was the case, while recognizing that one could just as well adopt Minkowski spacetime as a basis for reasoning about physical processes. The choice facing scientists, Poincaré argued in 1912, was not between two theories, or two classes of theories, but a conventional one between spacetimes (Walter, 2009).
Acknowledgments
The impetus for this paper was provided by the discovery of Vergne’s
long-lost notebooks by Jérôme de la Noë. The third section of the
paper benefited from discussions with Olivier Darrigol.
Notes
- 1 Poincaré to Lorentz, ca. April 27, 1905 (Walter et al., 2007, §2-38-2).
- 2 See (Langevin, 1905), referred to in (Poincaré, 1906b, 151).
- 3 “Vous supposez . Langevin suppose . J’ai essayé pour conserver l’unité de temps, mais cela m’a conduit à des conséquences inadmissibles.” The symbols and were defined to be numerical constants: , where is the vacuum speed of light, and is frame velocity, while was defined by Lorentz to be a function of , for , differing from unity for small velocities by a second-order quantity at most (Lorentz, 1904, 813).
- 4 See Cuvaj (1970, 74), Wright (1975, 453), Darrigol (1995; 2006; 2012), Damour (2005), Pierseaux (2005), and Rougé (2008).
- 5 The three public presentations of the light ellipse are the following: (1) lectures at the Paris Faculty of Sciences, 1906–1907, student notes of which were edited by Marguerite Chopinet (1953), (2) a plenary lecture delivered at the annual meeting of the Association française pour l’avancement des sciences, published in two versions (Poincaré, 1909, 1910a), and (3) and lectures delivered at the École supérieure des postes et des télégraphes in Paris in June, 1912, published posthumously as (Poincaré, 1913). The light ellipse appeared first in print in a popular article on the dynamics of the electron (Poincaré, 1908a), reedited in the essay collection Science et méthode (Poincaré, 1908b).
- 6 For a notable exception, see (Chang, 1993).
- 7 Henri Vergne (1879–1943) obtained his Ph.D. in mathematical sciences at the Paris Faculty of Sciences in 1909 (Vergne, 1909), and edited Poincaré’s 1910–1911 lectures on cosmogony for publication (Poincaré, 1911). Vergne later joined the faculty of the École Centrale in Paris, and served as president of the French Mathematical Society in 1939.
- 8 Vergne’s three notebooks were discovered in 2012 in the archives of the Bordeaux Observatory by Jérôme de la Noë, who arranged for their transfer to the Poincaré Archives.
- 9 “Alors je prends une surface rigoureusement sphérique. Je la mesure avec mon mètre: dans la direction du mouvement, mon mètre sera contracté de : sa longueur vraie sera devenue . Donc mon diamètre dans le sens du mouvement aura pour longueur mesurée . Dans le sens perpendiculaire la longueur mesurée sera 1. Donc une sphère paraîtra un ellipsoïde allongé dans le sens du mouvement.” The factor is defined to be , using modern notation.
- 10 For example, in Chopinet’s edition of Vergne’s diagram, the longitudinal radius is assigned length . Cuvaj, who referred to Chopinet’s edition, considered that measurement of the light shell was performed by comoving observers (Cuvaj, 1970, 74).
- 11 I agree here with Darrigol (2012).
- 12 Using the relations specified in Figure 3, we have Rearranging the latter expression in terms of , we find , and substituting the value of from (3) we obtain Poincaré’s expression (4) for apparent time, .
- 13 “De même est le temps apparent puisq’en 2 points le temps apparent diffère d’un quantité proport[ionnel] à l’abscisse.”
- 14 “Je suppose que je fasse l’échange des signaux: j’aurai p[ou]r le retour de en : (car l’abscisse a un signe). Ici . Donc la différence est rigoureusement proport[tionnel] à la différence des abscisses, et sans négliger le carré de l’abérration.”
- 15 In 1912, Poincaré singled out the set of events which can be neither the cause nor the effect of other given events, and attributed its discovery to the employment of a four-dimensional (3+1) vector space (Walter, 2009).
- 16 “Donc Lorentz suppose que tous les corps subissent dans la direction du mouvement une contraction proport. au carré de la vitesse. Alors les longueurs sont altérées, et les temps sont altérés par l’impossibilité de régler vraiment les montres, ce qui fait que la vitesse apparente de la lumière est constante. Alors nous effectuons une transformation de Lorentz : les transfor. de Lorentz doivent former un groupe, tel que l’on ait identiquement .”
- 17 “[I]l est impossible d’échapper à cette impression que le principe de relativité est une loi générale de la Nature, qu’on ne pourra jamais par aucun moyen imaginable mettre en évidence que des vitesses relatives, et j’entends par là non pas seulement les vitesses des corps par rapport à l’éther, mais les vitesses des corps les uns par rapport aux autres.”
- 18 Poincaré denoted the true time at which the body reached point by , and the true time at which the body attained point by , such that the elapsed true time for the body’s displacement between points and is . By comparison with (4), , and since is the true elapsed time, , we have . Likewise, Poincaré denoted the times of passage of the body in terms of true time, . The time at which the body reaches point is for observer and for observer . The time at which the body reaches point is for observer , and for observer . Subtracting the time of the body’s passage through as marked by observer from the time of passage of the body through as marked by observer results in Poincaré’s value for trip duration from to , .
- 19 Hilbert to Poincaré, 25 February, 1909, henripoincarepapers.univ-nantes.fr/chp/text/hilbert-1909-02-25.html. On research traditions in mathematics and mathematical physics in Göttingen at the turn of the twentieth century, see Rowe (1992) and Corry (2004).
- 20 For a review of Poincaré’s activity at the Bureau of Longitudes, see Galison (2003), and for discussion of his engagement with contemporary technological issues, including wireless telegraphy, see Gray (2013, 177).
- 21 “ peut se croire au repos et la vitesse apparente de sera, pour lui, 400000 kilomètres. Si connaît la mécanique nouvelle il se dira: a une vitesse qu’il ne peut atteindre, c’est donc que moi aussi je suis en mouvement. Il semble qu’il pourrait décider de sa situation absolue. Mais il faudrait qu’il puisse observer le mouvement de lui-même; pour faire cette observation et commencent par régler leurs montres, puis envoie à des télégrammes pour lui indiquer ses positions successives; en les réunissant, peut se rendre compte du mouvement de et tracer la courbe de ce mouvement. Or les signaux se propagent avec la vitesse de la lumière; les montres qui marquent le temps apparent varient à chaque instant et tout se passera comme si la montre de avançait.”
- 22 “Supposons maintenant un observateur entraîné dans la même translation que le corps lumineux. […] Des surfaces d’onde sembleront donc à notre observateur allongées dans le sens du mouvement; elles lui paraîtront ellipsoïdales. Tous ces ellipsoïdes seront homothétiques entre eux, et le corps lumineux en occupera un foyer. Dans ces conditions, un théorème de géométrie très simple montre que le temps apparent que la lumière mettra à aller de en , c’est-à-dire la différence entre le temps local en au moment du départ de , et le temps local en au moment de l’arrivée en , que ce temps apparent, dis-je, est le même que si la translation n’existait pas, ce qui est bien conforme au principe de relativité.”
- 23 “Mais ceci n’est pas suffisant, il faut encore supposer que l’on a: . L’introduction du coefficient revient à admettre que les phénomènes mécaniques sont accélérés par un mouvement de translation. Les constantes et dépendront de , et continue à dépendre de la position du point. Ceci rend compte de la compensation tout au moins en optique.”
- 24 “Nous voulons que le temps apparent soit le même que si l’on était au repos, c’est-à-dire que l’on ait : .”
- 25 From (9) and , we can write: and by inspection of Figure 6: Letting , we obtain: (11) Recalling the identity , along with (11), we find: (12) The published notes of Poincaré’s lectures at the ESPT do not develop the argument beyond (12), but if we recall the values of the parameters (reintroducing ): , , and , we find the transformation: Recalling that , and , the latter equation is seen to be equivalent to (4), which can be rearranged to give the modern Lorentz transformation (6), as shown above.
- 26 For an overview, see Staley (2008).
References
- From Maxwell to Microphysics. University of Chicago Press, Chicago. link1 Cited by: §2.
- A misunderstood rebellion: the twin-paradox controversy and Herbert Dingle’s vision of science. Studies in History and Philosophy of Science 24, pp. 741–790. Cited by: endnote 6.
- Henri Poincaré, Les limites de la loi de Newton. Bulletin astronomique 17 (3), pp. 121–269. link1 Cited by: endnote 5.
- David Hilbert and the Axiomatization of Physics (1898–1918): From Grundlagen der Geometrie to Grundlagen der Physik. Kluwer, Dordrecht. Cited by: endnote 19.
- On the electromagnetic mass of a moving electron. Philosophical Magazine 14, pp. 538–547. link1 Cited by: §2.
- A History of Relativity: The Role of Henri Poincaré and Paul Langevin. Ph.D. Thesis, Yeshiva University, New York. Cited by: endnote 10, endnote 4.
- Einstein, 1905–2005. Birkhäuser, Basel. Cited by: O. Darrigol (2006).
- Si Einstein m’était conté. le cherche midi, Paris. Cited by: endnote 4.
- The electrodynamic revolution in Germany as documented by early German expositions of ‘Maxwell’s theory’. Archive for History of Exact Sciences 45, pp. 189–280. Cited by: §2.
- Henri Poincaré’s criticism of fin de siècle electrodynamics. Studies in History and Philosophy of Modern Physics 26, pp. 1–44. Cited by: §2, endnote 4.
- The mystery of the Einstein-Poincaré connection. Isis 95 (4), pp. 614–626. Cited by: §1.
- The genesis of the theory of relativity. See Einstein, 1905–2005, Damour et al., Progress in Mathematical Physics, Vol. 47, pp. 1–32. Cited by: endnote 4.
- Poincaré and light. See Poincaré, 1912–2012, Duplantier, Séminaire Poincaré, Vol. 16, pp. 1–43. Cited by: §4, endnote 11, endnote 4.
- Poincaré, 1912–2012. École polytechnique, Palaiseau. Cited by: O. Darrigol (2012).
- Zur Elektrodynamik bewegter Körper. Annalen der Physik 322, pp. 891–921. link1 Cited by: §2.
- Relativitätsprinzip und die aus demselben gezogenen Folgerungen. Jahrbuch der Radioaktivität und Elektronik 4, pp. 411–462. Cited by: §4.
- Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips. Annalen der Physik 328, pp. 197–198. Cited by: §4.
- Einstein’s Clocks and Poincaré’s Maps: Empires of Time. Norton, New York. Cited by: endnote 20.
- Henri Poincaré: A Scientific Biography. Princeton University Press, Princeton. link1 Cited by: endnote 20.
- École nationale supérieure des PTT: histoire de la naissance et de la formation d’un corps de l’État, 1888–1988. Éditions Hervas, Paris. Cited by: §5.
- The Significance of the Hypothetical in the Natural Sciences. Walter de Gruyter, Berlin. Cited by: S. A. Walter (2009).
- Sur l’origine des radiations et l’inertie électromagnétique. Journal de physique théorique et appliquée 4, pp. 165–183. link1 Cited by: endnote 2.
- Vorlesungen über continuierliche Gruppen mit geometrischen und anderen Anwendungen. Teubner, Leipzig. link1 Cited by: §1.
- Versuch einen Theorie der elektrischen und optischen Erscheinungen in bewegten Körpern. Brill, Leiden. link1 Cited by: §2.
- Electromagnetic phenomena in a system moving with any velocity less than that of light. Proceedings of the Section of Sciences, Koninklijke Akademie van Wetenschappen te Amsterdam 6, pp. 809–831. link1 Cited by: endnote 3.
- Einstein, Lorentz, and the electron theory. Historical Studies in the Physical Sciences 2, pp. 41–87. link1 Cited by: §2.
- H.A. Lorentz and the electromagnetic view of nature. Isis 61, pp. 459–497. link1 Cited by: §2.
- On the relative motion of the earth and the luminiferous ether. American Journal of Science 34, pp. 333–345. link1 Cited by: §2.
- Die Grundgleichungen für die electromagnetischen Vorgänge in bewegten Körpern. Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, pp. 53–111. link1 Cited by: §4.
- Special relativity: Einstein’s spherical waves versus Poincare’s ellipsoidal waves. Annales de la Fondation Louis de Broglie 30 (3–4), pp. 353–379. link1 Cited by: endnote 4.
- La théorie de Lorentz et le principe de réaction. Archives néerlandaises des sciences exactes et naturelles 5, pp. 252–278. link1 Cited by: §2.
- Les relations entre la physique expérimentale et la physique mathématique. Revue générale des sciences pures et appliquées 11, pp. 1163–1175. link1 Cited by: §2.
- Électricité et optique: la lumière et les théories électrodynamiques. Carré et Naud, Paris. link1 Cited by: §2.
- L’état actuel et l’avenir de la physique mathématique. Bulletin des sciences mathématiques 28, pp. 302–324. link1 Cited by: §2.
- Sur la dynamique de l’électron. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 140, pp. 1504–1508. link1 Cited by: §1, §3.
- La Science et l’hypothèse. Flammarion, Paris. Cited by: §2.
- Sur la dynamique de l’électron. Rendiconti del Circolo matematico di Palermo 21, pp. 129–176. link1, link2 Cited by: §1, §3, §4, endnote 2.
- La dynamique de l’électron. Revue générale des sciences pures et appliquées 19, pp. 386–402. link1 Cited by: §4, endnote 5.
- Science et méthode. Flammarion, Paris. link1 Cited by: endnote 5.
- La mécanique nouvelle. Revue scientifique 47-2 (6), pp. 170–177. link1 Cited by: §4, endnote 5.
- La mécanique nouvelle. Revue électrique 13, pp. 23–28. link1 Cited by: endnote 5.
- Sechs Vorträge über ausgewählte Gegenstände aus der reinen Mathematik und mathematischen Physik. Teubner, Leipzig/Berlin. link1 Cited by: §4.
- Leçons sur les hypothèses cosmogoniques. Hermann, Paris. link1 Cited by: endnote 7.
- L’espace et le temps. Scientia (Rivista di Scienza) 12 (25), pp. 159–170. link1 Cited by: §4.
- La dynamique de l’électron. Dumas, Paris. link1 Cited by: Figure 6, §5, §5, §5, endnote 5.
- Relativité restreinte : la contribution d’Henri Poincaré. Éditions de l’École polytechnique, Palaiseau. Cited by: endnote 4.
- David Hilbert on Poincaré, Klein, and the world of mathematics. Mathematical Intelligencer 8, pp. 75–77. Cited by: §4.
- Felix Klein, David Hilbert, and the Göttingen mathematical tradition. Ph.D. Thesis, City University of New York, New York. Cited by: endnote 19.
- Einstein’s Generation: The Origins of the Relativity Revolution. University of Chicago Press, Chicago. Cited by: endnote 26.
- Contribution à la théorie des ondes liquides. Ph.D. Thesis, Faculté des sciences de Paris, Paris. Cited by: endnote 7.
- La correspondance d’Henri Poincaré, Volume 2: La correspondance entre Henri Poincaré et les physiciens, chimistes et ingénieurs. Birkhäuser, Basel. link1, link2 Cited by: §2, §2, §2, endnote 1.
- Hypothesis and convention in Poincaré’s defense of Galilei spacetime. See The Significance of the Hypothetical in the Natural Sciences, Heidelberger and Schiemann, pp. 193–219. link1 Cited by: §6, endnote 15.
- Henri Poincaré: A Developmental Study of His Philosophical and Scientific Thought. Ph.D. Thesis, Harvard University, Cambridge MA. Cited by: endnote 4.