Henri Poincaré’s student notebooks, 1870–1878
Philosophia Scientiae 1(4) (1996), 1–17
Abstract
An overview is presented of the origin and contents of seventeen notebooks kept by Henri Poincaré while a student in Nancy and in Paris, from 1870 to 1878.
Introduction
A well-known anecdote concerning the young Henri Poincaré recounts his habit of listening to lectures with arms crossed, while casting, one supposes, a skeptical eye upon the professor and his slate. The story would have it that Poincaré was a child prodigy, poised to spring from his fertile imagination those contributions to mathematics and physics that the next four decades would unfold in a declension of timeless genius.11endnote: 1 The anecdote was recounted in Lucien de la Rive’s necrology of Poincaré (La Rive 1914, 160), but its origin remains a mystery. Does the legend have anything to do with the historical neglect of Poincaré’s education? Some of the indifference is certainly due to the absence of significant documentary sources. But as it turns out, contrary to the anecdote, Poincaré did not have his arms crossed at all, because he was busy taking lecture notes, as demonstrated by the recent discovery of seventeen volumes of these notes. This essay briefly summarizes the contents of Poincaré’s school notebooks and their relation to other sources, and examines their historical significance.22endnote: 2 The entire notebook collection, including inserted leaves, may be consulted on microfilm (16mm) at either the Poincaré Archives in Nancy, or the Niels Bohr Library in College Park, Maryland. The author is grateful to Mr. François Poincaré for making the notebooks available for filming. A detailed presentation of notebook contents is found in the appendix.
1 Overview of the notebooks
While the sheer volume of the collection–4500 pages–prohibits a detailed résumé, an idea of the contents of the notebooks and their provenance may be obtained from Table 1.
| Item | Year | School | Subject | Lecturer | Pages | Total |
|---|---|---|---|---|---|---|
| 1 | 1870-3 | Lycée |
Geometry / Mechanics |
Lecomte [?] / Lefebvre |
314/120 | 438 |
| 2 | 1871-3 | Lycée |
Arithmetic |
Lecomte or Elliot |
376 | 376 |
| 3 | 1871-2 | Lycée |
Chemistry / Botany |
Lecomte |
242/62 | 304 |
| 4 | 1871-2 | Lycée |
Logarithms / Geometry; Cosmography |
Lecomte |
40/52; 120 | 312 |
| 5 | 1872-3 | Lycée |
Physics |
Lefebvre |
278 | 278 |
| 6 | 1872-3 | Lycée |
Experimental Physics / Chemistry |
Lefebvre |
104/130 | 234 |
| 7 | 1872-3 | Lycée |
Algebra / Geometry |
Elliot |
260/196 | 456 |
| 8 | 1872-3 | Lycée |
Geometry |
Elliot |
153 | 194 |
| 9 | 1875-7 | Mines |
Docimasy |
Carnot |
372 | 372 |
| 10 | 1877-8 | Mines |
Utilization of Mines & Machines / Legislation & Industr. Econ. |
Haton de la Goupillière; Dupont |
128/48 | 192 |
| 11 | 1875-7 | Mines |
Utilization of Mines & Machines |
Haton de la Goupillière |
234 | 234 |
| 12 | 1875-7 | Mines |
Metallurgy |
Lan |
210 | 230 |
| 13 | 1875-7 | Mines |
Geology / Palæontology |
De Chancourtois / Bayle |
94 | 130 |
| 14 | 1875-7 | Mines |
Mineralogy / Geology |
Mallard / De Chancourtois |
119/110 | 238 |
| 15 | 1877-8 | Mines |
Legislation & Industr. Econ. |
Dupont |
124 | 140 |
| 16 | 1876-8 | Mines |
Industr. Constr. & Railroads / Legislation & Industr. Econ. |
Resal / Dupont |
100/40 | 186 |
| 17 | 1877-8 | Mines |
Indust. Constr. & Railroads / Agriculture, Drainage & Irrigation |
Resal / Delesse |
152/5 | 184 |
|
Total |
4178 | 4498 |
The school and estimated writing period for each notebook is listed in the table, as well as the primary subjects covered, the lecturer’s name, and the number of pages.33endnote: 3 For the École des Mines the course titles and professors have been established based on Poincaré’s gradesheet, published in Le Livre du Centenaire (Paris: Gauthier-Villars, 1955), p. 259, combined with information in the Registre Matricule for professors at the École des Mines (Archives de l’École des Mines de Paris), and Aguillon (1889, 228ff). The notebooks often contain notes on subjects other than those listed; for this reason, the value in the last column of the table is not always equal to the sum of the numbers in the next-to-last column. Seven notebooks were written while Poincaré was a student at the Lycée de Nancy, while the remaining volumes were established at the École des Mines in Paris. No notebooks have been recovered from the years 1873 to 1875, when Poincaré was a student at the École Polytechnique.44endnote: 4 From the letters Poincaré wrote to his mother during this period, however, it is clear that Poincaré also kept notebooks while at Polytechnique.
The table indicates an array of subjects studied by Poincaré, ranging from botany, algebra and cosmography in the early years, followed by mining legislation and economics in the late 1870s. At the Lycée de Nancy, where the scientific sections had long outnumbered the literary ones (Anderson 1975, 99), Poincaré and his eight hundred classmates received some of the best scientific instruction available in France. Catering, perhaps, to his taste for literature and the dramatic arts, Poincaré followed the literary track (Bellivier 1956, 89). This choice, quite common at the time for male offspring of the haute bourgeoisie (Shinn 1980, 50), allowed Poincaré to learn Greek and Latin instead of chemistry, and did not prevent him from obtaining passing marks for the scientific baccalauréat examination in 1871.
The Lycée de Nancy’s preparatory program of mathématiques spéciales had an excellent reputation, sending as many as sixteen of its young men a year to the prestigious École Polytechnique.55endnote: 5 In Poincaré’s graduation class six students attended Polytechnique (Registre matricule, Archives de l’École Polytechnique). The program’s professors were both graduates of the elite École Normale Supérieure; Elliot (ENS 1866) taught mathematics, while Lefebvre (ENS 1852) taught mechanics, physics and chemistry.66endnote: 6 They would both go on to more coveted posts: Elliot to the university system (Besançon), and Lefebvre to the Lycée Hoche in Versailles. The principal, Davau, was also a graduate of the École Normale, and an agrégé de mathématiques (Bellivier 1956, 107).
Poincaré’s time at the Lycée was marked by great upheaval in France. The franco-prussian war (1870-1873), during which France lost territory in the Alsace-Lorraine region, led the Lycée to welcome several hundred refugee students, including Paul Appell.77endnote: 7 Paul Appell, whose elder brother Charles was convicted of espionage and imprisoned in Germany, later described the impact of the war in vivid terms (Appell 1923). The Lorraine city of Nancy was occupied, and the Lycée itself was temporarily requisitioned for troop billeting. The effect of these events on Poincaré is unknown, but the war surely marked the end of a protected childhood. The memoirs of his sister Aline recount the events surrounding the negotiations between Nancy’s burghers (including her father, a professor on the medical faculty) and the enemy. Fearing the imminent sack of the city, her mother entrusted the family jewels and deeds of property to Henri’s booksack, enjoining him to convey them to a safer place, imagining, Aline writes, that the soldiers would not molest a mere child. Young Henri managed to save the family fortune, so the story goes, by wandering the streets of Nancy with his little sister in hand, until the danger had passed.
A few general remarks may be made concerning the appearance and style of the notebooks written from 1870 to 1873. They were written by a diligent, attentive student, who took notes in a hurried but legible hand, following what appears to have been well-organized classroom instruction. Many of the notebooks contain verbatim records of lectures, including sentences containing blanks where the notetaker fell behind the pace of the presentation, or did not catch part of a phrase. There are few misspellings or grammatical errors in any of the notebooks. The possible exception to the rule is the spelling of proper names, yet in misspelling the names of Foucault, Rühmkorff and Fraunhofer, Poincaré was far from exceptional, as attested by scientific correspondence of the period.
Poincaré was not one to confuse his writing genres, in that none of the notebooks may be mistaken for a diary, or even a datebook. There is nothing of a private nature to be found here, no commentary of any type. Lectures were transcribed, in other words, but nothing indicates that the transcription was ever read by the scribe.
The mathematics notebooks from the Nancy period are of particular interest, due to the preservation of Poincaré’s examination papers from this same class. A comparison of the two sources allows a rare view into the way the young Poincaré learned his lessons. The test questions required, in general, little more than a good memory of the examples presented during classtime, and here Poincaré proved himself capable of accurately recalling the demonstration required for the occasion. From time to time, he became careless in his work, but this occurred only rarely, and his efforts were often awarded with the highest possible grade.
According to his fellow student, Paul Appell (1921, 2), Poincaré displayed great interest in the physics course, which he considered excellent, while the chemistry class lacked distinction, Appell said, and did not inspire his friend. By the end of his studies at the Lycée de Nancy, Poincaré had acquired knowledge “of a distinguished order,” in the opinion of the jury for the Concours général de mathématiques spéciales in 1873.88endnote: 8 The opinion of the jury, composed of Bouquet, Briot, Puiseux and Prollier, is noted on Poincaré’s composition (Poincaré 1925). This particular competition had been won by Poincaré the previous year. Ranked first after the entrance exam for the École Polytechnique, Poincaré was classed fifth for the École Normale Supérieure.
Although a professor at the University of Nancy warned Poincaré that what he would learn there would be of little use to him in later life (Bellivier 1956, 131), he chose to attend the École Polytechnique, where he studied for two years under some of the leading names in French mathematics and physics.99endnote: 9 Poincaré’s science professors at Polytechnique were Hermite (Analysis), Cornu (Physics), Resal (Mechanics), Mannheim (Geometry), Faye (Astronomy) and Fremy (Chemistry). The highly competitive, formative milieu of Polytechnique was one in which Poincaré thrived, as witnessed by the extensive correspondence with his mother.1010endnote: 10 Transcriptions of extracts of this correspondence may be found in Bellivier’s biography of Poincaré. No notebooks have been located from this period, as mentioned above.
The École Polytechnique served as a feeder school for the École des Mines; the top-ranked graduates of Polytechnique almost invariably chose to continue their studies at this institution, rather than at the rival engineering school Ponts et Chaussées (Shinn 1980, 186-7). After graduating second in a class of around two hundred students, Poincaré naturally decided to continue his studies at the École des Mines.
The students from Polytechnique enrolling at Mines embarked upon a three-year course of study designed to prepare them for a technical or administrative career in the mining or construction industries. Graduates were assured of high-profile careers offering excellent pay and social advantages, yet those who went on to become mine inspectors did so at great risk. Bonnefoy, Poincaré’s rival at Polytechnique, perished in the course of investigating a mining accident.
Among Poincaré’s professors at Mines was one known to him from Polytechnique: Henri Resal (1828-1896), who edited the Journal de mathématiques pures et appliquées. It is perhaps no accident that Resal’s journal was one of the first to publish Poincaré’s work (Gilain 1991, 216). Teaching mechanics at Polytechnique and industrial engineering at Mines, Resal’s accumulation of academic appointments was a common practice among leading Parisian professors of scientific and technical subjects.1111endnote: 11 The accumulation of posts is one of the many institutional apects of French mathematics examined by Gispert (1991).
The study of mathematics was not a part of the curriculum at Mines, and in spite of the intervention on his behalf by Ossian Bonnet, Poincaré was not allowed to skip any of the required lectures in order to follow other subjects at the Sorbonne. In fact, the only course requiring any mathematics was mineralogy, including mathematical and physical crystallography. Poincaré, unlike his fellows, mastered this subject to the instructor’s satisfaction (Bellivier 1956, 177).
According to Paul Appell’s recollection (1925, 29), Poincaré paid less than full attention to the lectures at Mines, but after all, he probably had no intention of pursuing a career as a mine inspector, as he affirmed in an interview many years later (Toulouse 1910, 29). The notebooks of the period reflect a certain lack of concentration, and are filled with hundreds of doodles. Much has been made of Poincaré’s putative inability to draw figures, yet numerous ink drawings attest to Poincaré’s ability to render with accuracy both solid objects (see Figure 1), and complex diagrams. The correspondence with his mother indicates that he made an effort to improve his drawing ability while at Polytechnique, and was satisfied with the result.
If the proliferation of doodles in the later notebooks is an indication of Poincaré’s lack of interest in the courses offered at Mines, no more may be said, at least for the moment, on the subject of Poincaré’s attitude toward his teachers and the topics they lectured on. No subjective comment or introspection may be found in either the Nancy notebooks, as mentioned above, or in the notebooks from the École des Mines. On the other hand, some of the material may be of use to the biographer. A number of loose leaves were inserted in the notebooks, including such items as letters, a school pass, a travel itinerary, a funeral announcement and a restaurant bill.1212endnote: 12 From a restaurant bill Poincaré’s wine consumption may be estimated, and he appears to have consumed no more than one glass of wine per meal (assuming a homogeneous distribution over the number of meals).
Studying on his own, Poincaré obtained the Licence ès sciences in his first year at Mines, and he continued to read the works of mathematicians, according to Appell (1925, 29).1313endnote: 13 For comparison, in 1865, France’s 16 science faculties graduated 100 Licence students, half of whom studied in Paris (Anderson 1975, 225). In 1877, he submitted a 111-page manuscript on partial differential equations for a prize competition organized by the Académie des Sciences (Molino 1991). In the course of the following year, he finished his studies at Mines, started work as a mine inspector, and defended his Ph.D. thesis at the Sorbonne.
Doodles and bills apart, what interest do Poincaré’s notebooks have for the scholar seeking to understand Poincaré’s scientific career? One area that suggests itself immediately is the study of Poincaré’s writings on school reform. Although his teaching career was conducted exclusively at the university level, Poincaré had strong opinions on the way scientific subjects ought to be taught in secondary school, and he expressed them on several occasions (Poincaré 1899, reed. in Petiau, ed, 1954, 129-133; 1904b).
The scholar interested in studying the intellectual atmosphere of the provincial French lycée in the nineteenth century will find much to ponder between the covers of Poincaré’s school notebooks. According to Appell, Poincaré was fond of natural philosophy as a student of mathématiques spéciales (Appell 1921). Appell mentioned in particular their shared fascination with the plurality of worlds hypothesis, which led the renowned astronomer and popular science writer Camille Flammarion and others–perhaps Poincaré himself–to reject Christian religion.1414endnote: 14 According to Crowe (1986, 557), Flammarion rejected Christianity because he felt it was incompatible with the existence of extraterrestrial life. Poincaré was brought up in a Catholic family, and confirmed at age eleven; when he became a public figure, his name was often associated with anti-clerical, republican values. Poincaré confessed to Dr. Toulouse in the late 1890s that while he believed in Christianity at the time of his confirmation, his belief had ceased by 1872 (Toulouse 1910, 143–144). In 1875, Poincaré met one of France’s most brilliant young philosophers, Émile Boutroux (1845-1921), who became his brother-in-law in 1878, and editor of his first philosophy paper in 1881 (Poincaré 1881).1515endnote: 15 See the correspondence between Poincaré and his mother in the Poincaré archives. Boutroux’s influence on Poincaré is discussed by Nye (1979). Poincaré’s philosophical reflection was both precocious and enduring, developing in tandem with his scientific interests.
The notebook devoted to the subject of cosmography holds particular interest in this respect, because it contents may be correlated with certain themes featured in Poincaré’s later writings. For example, the first pages record the introduction of the notion of a celestial sphere:
We are certain that this sphere is only fictional, for, apart from the fixed stars there are also some that are in motion [..]. Nevertheless, as this sphere is a convenient geometrical instrument, we retain it in cosmography and suppose all stars are transported along their radial vector to the celestial sphere.1616endnote: 16 “Nous sommes certains que cette sphère n’est qu’une pure conception ; car outre les étoiles fixes il y en a d’autres qui sont mobiles [..]. Néanmoins comme cette sphère est un instrument géométrique commode, on la conserve en cosmographie et on suppose tous les astres transportés sur leur rayon vecteur sur la sphère céleste.”
Poincaré was thus introduced at a tender age to the advantages of an instrumental approach to mathematics.
In another passage from the same notebook, the principle of relative motion is discussed with respect to the Earth’s orbit. Poincaré notes (see Figure 2) that the description of planetary motion in Ptolemy’s system is one of “extreme complication.” Then, as “mechanical proof” of terrestrial translational motion, he records the following.
It is not indifferent whether an observer is at rest or in motion, in his appreciation of light. If he is in motion, his velocity composes with that of light, and this brings about a deviation of light.1717endnote: 17 “Il n’est pas indifférent qu’un observateur soit fixe ou mobile dans son appréciation de la lumière. S’il est en mouvement sa vitesse se compose avec celle de la lumière et il en résulte une déviation de la lumière.”
This passage bears witness to the interest provoked by contemporary theories and experiments concerned with the proper motion of the Earth.1818endnote: 18 Hippolyte Fizeau (1819-1896) confirmed the value of the Fresnel coefficient in a famous experiment of 1851. Additional results on ether drag were provided by Respighi (1861), Hoek (1868), Airy (1871) et Mascart (1872); for references, see Whittaker (1951). The elementary treatment of this subject remained within reach of the students, and none of the contemporary theories of stellar aberration seem to have been mentioned.
Nonetheless, the subject may have sparked Poincaré’s imagination. Four years later at the École Polytechnique, in lectures given by the young physicist Alfred Cornu (1841-1902), Poincaré was exposed to the fundamentals of the wave theory of light, including the problem of ether drag and the solution offered by Fresnel’s drag coefficient.1919endnote: 19 Autograph notes to Cornu’s 1874-1875 lectures, in the Archives of the École Polytechnique. According to a retrospective account, with the aid of a fellow student, Poincaré designed and executed an optical experiment to demonstrate the translation of the Earth with respect to the luminiferous ether.2020endnote: 20 On Poincaré’s experiment to detect motion of the Earth with respect to the ether see Walter (1999). The null result of such experiments–in particular that of Albert A. Michelson and Frank Morley in 1887–was among the factors that led Poincaré to announce a new principle of physics, which he called “the principle of relativity” (Poincaré 1904a).
On the basis of Poincaré’s student notes on the convenience of hypotheses, relative motion and aberration one might be tempted to conclude that they are the source of later developments of these notions in his published writings. From a biographical standpoint, it is surely remarkable that several notions present in Poincaré’s mature works in physics and philosophy were taught to him in adolescence. A less speculative approach, however, would be to consider the appearance of these and other themes in secondary school science curricula with respect to the intellectual preoccupations of late nineteenth century scientists, both inside and outside of the French community. To my knowledge, no attempt has been made to examine in a synoptic fashion the school notebooks of scientists active in this period, but such an effort might shed light on the relation of curriculum reform to the historical development of the exact sciences.2121endnote: 21 For an investigation of the German case along these lines see Pyenson (1983).
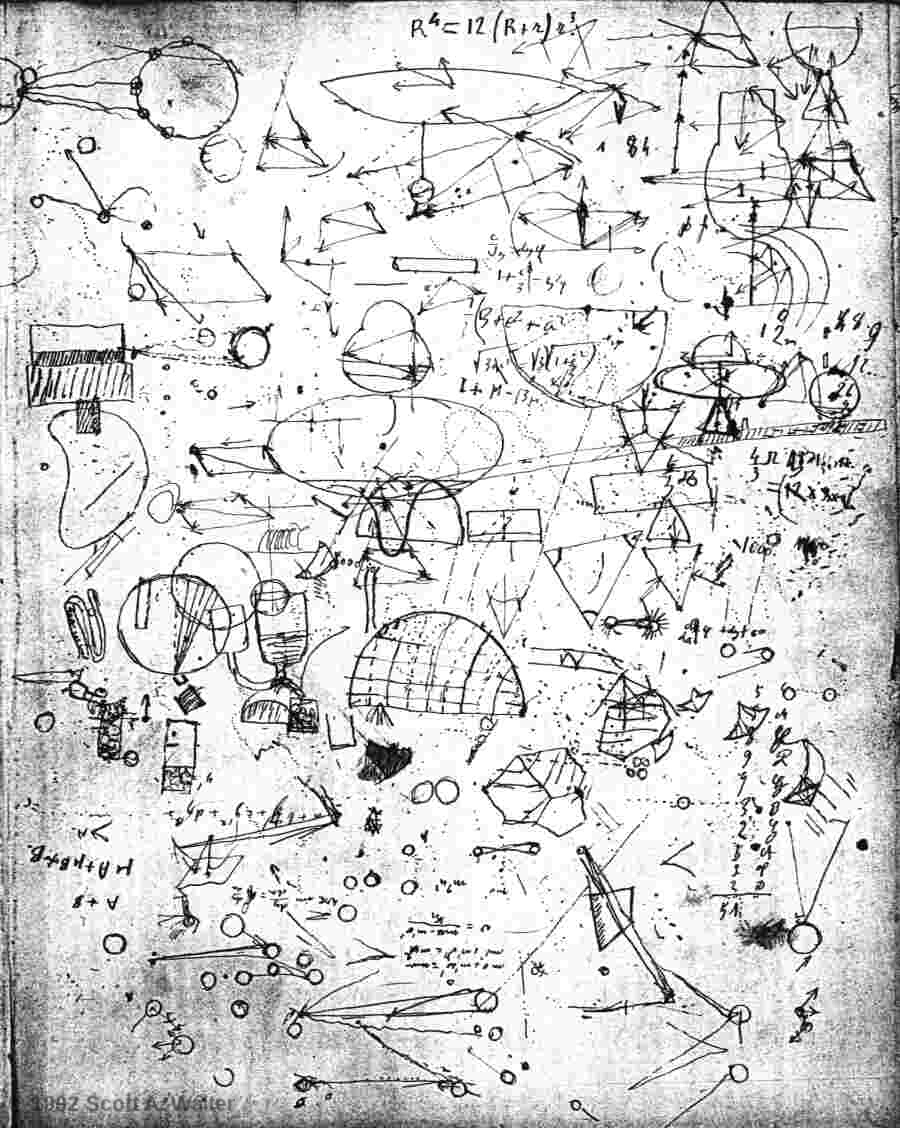

2 Appendix: Table of contents for Henri Poincaré’s student notebooks
I. Notebooks from the Lycée de Nancy, 8 vols., 1870–1873.
1. Lycée de Nancy, ca. 1870-1873, 438 pp. Geometry (314 pp.), including plane geometry, geometry of space, and spherical geometry. Mechanics (120 pp.): law of inertia; division of mechanics; axioms of statics; decomposition of forces; moments; center of gravity; simple machines; kinematics; relative motion; dynamics; momentum; parabolic motion; work; perpetual motion (impossibility of); living force.
2. Mathématiques élémentaires or spéciales, ca. 1871-1873, 376 pp. from a course in arithmetic.
3. Mathématiques élémentaires, ca. 1871-1872, 304 pp. Contents include 240 pp. from an introductory chemistry course, including a short section on the Dalton’s atomic theory; 60 pp. from an introductory botany class, and 4 pp. on magnetized needles and galvanometry.
4. Mathématiques élémentaires, ca. 1871-1872, 312 pp. Contains approximately 40 pp. from a course on logarithms, 50 pp. of descriptive geometry, 120 pp. on cosmography, and 6 pp. on the structure of magnets. One inserted page has several figures and equations, and several lines written in German, in Poincaré’s hand. The cosmography course covered the following subjects: notion of the celestial sphere (and its mathematical convenience); instruments (telescopes, theodolites); meridian determination; sidereal time; demonstration of the Earth’s motion (Foucault’s pendulum, and the trajectory of free-falling bodies); determination of right ascension and declination; form and measument of the Earth; determination of the Earth’s radius (Newton, Richet, expeditions of Bouguer, Clairaut and Maupertuis); orthographic and stereographic projections; influence of the atmosphere on astronomical observation (refraction, reflection, absorption); the Sun; elliptical motion (Kepler); measurement of the apparent diameter of the Sun; precession of the equinox (Hipparchus); nutation (Bradley); time measurement (solar day); calendars; sundials; gnomons; determination of solar parallax; physical constitution of the Sun; sunspots; solar rotation; zodiacal light; seasons; relative motion; simplicity of heliocentric vs. Ptolmaic system; stellar aberration; theory of the moon; elliptical motion.
5. Mathématiques spéciales. 1872-1873, 278 pp. from an introductory physics course. This course was probably accompanied by an experimental course, which produced another notebook (#6). The following subjects are covered: definitions of force and mass, gravitation, resistance to motion, inclined plane, Atwood’s machine, Morin’s machine, the pendulum, Huyghen’s formula, variations in the Earth’s gravitational force, centripetal force, levers, moments, center of gravity, scales, hydrostatics, Haldat’s apparatus, a hydrostatic paradox, vases communiquants, law of Archimedes, capillarity, specific weight, areometers, atmospheric pressure, barometers, compressible gases, Mariotte’s law, manometers, theory of pneumatic machines, Torricelli’s theorem, siphons, Mariotte’s vase, Héron’s fountain. Heat: definition of temperature, thermometers, dilatation in liquids, solids, and gases; changes in state; vapors; Dalton’s apparatus; vaporization; calefaction; gas density; specific weight of air; calorimetry; specific heat of liquids; Dulong and Petit’s law; latent heat of fusion and vaporisation; heat sources; mechanical sources of heat; equivalence of work and heat; hygrometry. Electricity: two-fluid hypothesis; electrical attraction and repulsion; Coulomb’s law; Biot’s verification; distribution of electricity; experiments with electricity; electroscopy; electrophore; electrical machine; conductors; Leiden flask; atmospheric electricity and lightning; magnetism; geomagnetism; inclination needle; resistance of conductors; Ohm’s law; batteries; chemical effects: electrolysis; discoveries made by Faraday, Lavoisier and Jacobi; heat production in batteries; electromagnetism; electromagnetic machines; Morse telegraph; Hugues telegraph; Ampère’s discovery of the action of currents on currents; Ampère’s law; Earth’s action on currents; solenoids; induced currents; Lenz’s law; Rühmkorff’s electric induction apparatus; rotational magnetism; Clarke’s machine. Acoustics; propagation speed of sound; string vibrations; musical scale; consonance and dissonance; harmonics; longitudinal vibrations. Optics: propagation of light in homogeneous media; speed of light; Roemer’s observation of Jupiter’s moons; Foucault’s method; definition of the ray of light; photometers; law of reflection; mirrors; refraction; double refraction; lenses; dispersion; solar spectrum; Fraunhofer lines; eyesight; microscopes; telescopes; daguerrotypes; radiant heat; image shift due to motion of the Earth; thermoscope; heat reflection, emission, absorption. Two inserts: (1) a single page with notes on the operating principle of a chemical hygrometer, and on meteorology. Numerous figures and equations unrelated to these subjects; (2) a single page with a schematic diagram and description of a refracting ray.
6. Mathématiques spéciales. 1872-1873, 233 pp., of which 128 pp. from an introductory chemistry course, and 104 pp. from an introductory experimental physics course covering the following subjects: precision measuring instruments; uniform motion; harmonic motion; decomposition of motion; force measurement; Poncelet’s dynamometer; Atwood’s machine; force decomposition; centripetal force; work; center of gravity; specific weight; mass; Poinsot’s theorem; conditions of equilibrium; moment of inertia; gravitation; influence of the Earth’s rotation on falling bodies; wind resistance; inclined plane; friction coefficient; simple pendulum; compound pendulum; measurement of at various locations; Kepler’s law; Newton’s law of attraction; variation of due to asphericity of the Earth; gravitational attraction inside the Earth; mass of the Earth; Cavendish’s method; the balance; hydrostatics; fluid equilibrium; hydraulic press; pressure on a submerged body; equilibrium of floating bodies; areometers; alcoholometers; air-bubble level; properties of gases; Torricelli’s experiment; barometers; Mariotte’s law; Dulong’s experiment; Arago’s experiment; compressed-air manometer; volumeter; pneumatic machines; liquid pumps; priming the pump; Torricelli’s theorem; Héron’s fountain; siphons; gas density; capillary action; static electricity; Franklin’s hypothesis; Coulomb’s balance; the Leiden jar; distribution of electricity; electrical influence [induction]; electroscopes; electric machines (Guericke, Ramsden, Nairne [?], Armstrong); Volta’s electrophore; machines of Bertsch, Carré, Holtz; condenser experiment and theory; electrical discharge; calorific effects; atmospheric electricity; Peltier’s electroscope; Franklin’s kite; lightning-rods; magnetism; the Gauss magnetometer; methods of measuring attraction (torsion, oscillations, Gauss’s method).
7. Mathématiques spéciales, 1872-73, 456 pp. Contents include 260 pp. from a class in algebra, 136 pp. from a course in analytic geometry (second-order surfaces) and 60 pp. from a class in trigonometry. Two inserts: (1) a short story (this may be a translation exercise from German to French), both sides covered with several figures and equations; (2) a school pass in the name of Poincaré, from the Lycée de Nancy, dated March 12, 1873, with several equations and figures.
8. Mathématiques spéciales, 1872-73, and 1905, 194 pp. Contains 126 pp. from a course in descriptive geometry, and 27 pp. from a course in analytic geometry. This notebook also has the text (35 pp.) of Poincaré’s introduction to the 1905 publication The Collected Mathematical Papers of George William Hill, written in a hand that is not Poincaré’s, and is dated March 1905. Inserted in this notebook is a faire-part of the death of H.-L.-M. Reiveilliez from Épinal, dated June 21, 1873, and on which appear numerous figures and equations in Poincaré’s hand (4 pp.).
II. Notebooks from the École des Mines, 9 vols., 1875–1888.
9. 1875–1877, 372 pp. from a course in docimasy taught by Carnot (b. 1839).
10. Ca. 1875–1878, 192 pp. Contents include 128 pp. on mining technology, including structural support of mineshafts, and safety precautions, 48 pp. on the economics of mine exploitation (1877–1878), and 16 pp. of notes for a laboratory course on mineralogy. Subjects discussed include the division of workgroups for independance and surveillance, technique for avoiding explosion of gas pockets, and the width of wood supports.
11. 1875–1877, 234 pp., of which 230 pp. are from a course on machine technology, including the following subjects: hydraulics, hydraulic motors, thermodynamics, Carnot cycle, fire-driven machines, strength of materials, torsion. There are also four pages of figures and equations apparently unrelated to machine technology.
12. 1875–1877, 230 pp., of which 210 are from a course in metallurgy, one page with mention of the theory of “trois feux” and Laplace’s theory on cosmogony, and 22 pp. from a laboratory course in docimasy.
13. 1875–1877, 130 pp. Contains 94 pp. from a course in geology and palæontology, 5 pp. on the “general theory of hydraulic motors,” 2 pp. of an English exercise in dictation, and 29 interspersed pages of figures, portraits, equations, tables, notes and numerical calculations. Four inserts: (1) a bill to M. Poincaré from the Maison Laveur, 6, rue des Poitevins, 6e. Guitard et Losset Table d’Hôte; (2) a letter to “Cher Monsieur Poincaré” dated May 11, 1877, from Frenier, including several equations and figures in Poincaré’s hand; (3) a half-page with differential equations and a figure, apparently extracted from the notebook; (4) a single page with a numerical calculation–in Poincaré’s hand–of the cost of a voyage by train in northern Italy. This notebook features numerous doodles, including a female portrait.
14. 1875–1877, 237 pp. Contents include 119 pp. from a course in mineralogy (1875-1876), including cristallography, optical phenomena in crystals, and 110 pp. from a geology course (1875–1877). Interspersed are 8 pp. of apparently unrelated differential equations and figures.
15. 1877–1878, 140 pp. The front cover indicates that this notebook belongs to Poincaré, and contains 124 pp. of notes from a course in Mining Legislation and Industrial Economy (1877–1878). Also contains a technical study of the Lalstah bridge (England), and exercises for a course in Military Fortification (1877–1878), including a two-page description and analysis of the defense of Paris.
16. 1877–1878, 186 pp. Contains 100 pp. from a course in mining technology, including a study of metal cables, and 40 pp. on the following subjects: expropriation, chrome, mining economics.
17. 1877–1878, 184 pp. The front cover indicates that this notebook belongs to Poincaré, and contains notes on a course in construction given by Henri Resal at the École des Mines during the academic year 1877–1878. Contains 152 pp. from a course in construction technology, including strength of materials, hydraulics and rail technology. Also contains: 10 pp. from a course in Military Fortifications (trench warfare); 11 pp. of statistics on global mining production, mining accidents, transportation costs and population; 5 pp. on the chemical composition of various animal fertilizers, probably from a course in Agriculture, drainage and irrigation (1877–1878), taught by Delesse (1817–1881).
Notes
- 1 The anecdote was recounted in Lucien de la Rive’s necrology of Poincaré (La Rive 1914, 160), but its origin remains a mystery.
- 2 The entire notebook collection, including inserted leaves, may be consulted on microfilm (16mm) at either the Poincaré Archives in Nancy, or the Niels Bohr Library in College Park, Maryland. The author is grateful to Mr. François Poincaré for making the notebooks available for filming.
- 3 For the École des Mines the course titles and professors have been established based on Poincaré’s gradesheet, published in Le Livre du Centenaire (Paris: Gauthier-Villars, 1955), p. 259, combined with information in the Registre Matricule for professors at the École des Mines (Archives de l’École des Mines de Paris), and Aguillon (1889, 228ff). The notebooks often contain notes on subjects other than those listed; for this reason, the value in the last column of the table is not always equal to the sum of the numbers in the next-to-last column.
- 4 From the letters Poincaré wrote to his mother during this period, however, it is clear that Poincaré also kept notebooks while at Polytechnique.
- 5 In Poincaré’s graduation class six students attended Polytechnique (Registre matricule, Archives de l’École Polytechnique).
- 6 They would both go on to more coveted posts: Elliot to the university system (Besançon), and Lefebvre to the Lycée Hoche in Versailles. The principal, Davau, was also a graduate of the École Normale, and an agrégé de mathématiques (Bellivier 1956, 107).
- 7 Paul Appell, whose elder brother Charles was convicted of espionage and imprisoned in Germany, later described the impact of the war in vivid terms (Appell 1923).
- 8 The opinion of the jury, composed of Bouquet, Briot, Puiseux and Prollier, is noted on Poincaré’s composition (Poincaré 1925). This particular competition had been won by Poincaré the previous year.
- 9 Poincaré’s science professors at Polytechnique were Hermite (Analysis), Cornu (Physics), Resal (Mechanics), Mannheim (Geometry), Faye (Astronomy) and Fremy (Chemistry).
- 10 Transcriptions of extracts of this correspondence may be found in Bellivier’s biography of Poincaré.
- 11 The accumulation of posts is one of the many institutional apects of French mathematics examined by Gispert (1991).
- 12 From a restaurant bill Poincaré’s wine consumption may be estimated, and he appears to have consumed no more than one glass of wine per meal (assuming a homogeneous distribution over the number of meals).
- 13 For comparison, in 1865, France’s 16 science faculties graduated 100 Licence students, half of whom studied in Paris (Anderson 1975, 225).
- 14 According to Crowe (1986, 557), Flammarion rejected Christianity because he felt it was incompatible with the existence of extraterrestrial life. Poincaré was brought up in a Catholic family, and confirmed at age eleven; when he became a public figure, his name was often associated with anti-clerical, republican values.
- 15 See the correspondence between Poincaré and his mother in the Poincaré archives. Boutroux’s influence on Poincaré is discussed by Nye (1979).
- 16 “Nous sommes certains que cette sphère n’est qu’une pure conception ; car outre les étoiles fixes il y en a d’autres qui sont mobiles [..]. Néanmoins comme cette sphère est un instrument géométrique commode, on la conserve en cosmographie et on suppose tous les astres transportés sur leur rayon vecteur sur la sphère céleste.”
- 17 “Il n’est pas indifférent qu’un observateur soit fixe ou mobile dans son appréciation de la lumière. S’il est en mouvement sa vitesse se compose avec celle de la lumière et il en résulte une déviation de la lumière.”
- 18 Hippolyte Fizeau (1819-1896) confirmed the value of the Fresnel coefficient in a famous experiment of 1851. Additional results on ether drag were provided by Respighi (1861), Hoek (1868), Airy (1871) et Mascart (1872); for references, see Whittaker (1951).
- 19 Autograph notes to Cornu’s 1874-1875 lectures, in the Archives of the École Polytechnique.
- 20 On Poincaré’s experiment to detect motion of the Earth with respect to the ether see Walter (1999).
- 21 For an investigation of the German case along these lines see Pyenson (1983).
References
- L’École des Mines de Paris: Notice historique. Dunod, Paris. Cited by: endnote 3.
- Education in France, 1848-1870. Clarendon, Oxford. Cited by: §1, endnote 13.
- Henri Poincaré, en mathématiques spéciales à Nancy. Acta mathematica 38, pp. 189–195. Cited by: §1, §1.
- Souvenirs d’un Alsacien 1858-1922. Payot, Paris. link1 Cited by: endnote 7.
- Henri Poincaré. Plon, Paris. Cited by: §1, §1.
- Henri Poincaré ou la vocation souveraine. Gallimard, Paris. Cited by: §1, §1, §1, endnote 6.
- The Extraterrestrial Life Debate 1750–1900: The Idea of a Plurality of Worlds from Kant to Lowell. Cambridge University Press, Cambridge. Cited by: endnote 14.
- La théorie qualitative de Poincaré et le problème de l’intégration des équations différentielles. Cahiers d’histoire et de philosophie des sciences 34, pp. 215–242. link1 Cited by: §1.
- La France mathématique : la Société mathématique de France (1870–1914). SFHST, Paris. link1 Cited by: endnote 11.
- The Expanding Worlds of General Relativity. Birkhäuser, Boston/Basel. Cited by: S. A. Walter (1999).
- Henri Poincaré : la carrière scientifique. Archives des sciences physiques et naturelles 38, pp. 159–163. link1 Cited by: endnote 1.
- La monadologie. Delagrave, Paris. Cited by: H. Poincaré (1881).
- Un manuscrit inédit d’Henri Poincaré. Comptes rendus de l’Académie des sciences, série générale: La vie des sciences 8, pp. 329–331. Cited by: §1.
- The Boutroux Circle and Poincaré’s conventionalism. Journal of the History of Ideas 40, pp. 107–120. Cited by: endnote 15.
- Œuvres d’Henri Poincaré, Volume 10. Gauthier-Villars, Paris. link1 Cited by: §1.
- Note sur les principes de la mécanique dans Descartes et dans Leibnitz. See La monadologie, Leibniz, pp. 225–231. link1 Cited by: §1.
- La logique et l’intuition dans la science mathématique et dans l’enseignement. Enseignement mathématique 1, pp. 157–162. link1 Cited by: §1.
- L’état actuel et l’avenir de la physique mathématique. Bulletin des sciences mathématiques 28, pp. 302–324. link1 Cited by: §1.
- Les définitions générales en mathématiques. Enseignement mathématique 6, pp. 257–283. link1 Cited by: §1.
- Concours général de 1873 : Copie de Henri Poincaré, élève du lycée de Nancy. Revue de mathématiques spéciales 36, pp. 1–6. link1 Cited by: endnote 8.
- Neohumanism and the Persistance of Pure Mathematics in Wilhelmian Germany. Amer. Phil. Soc., Philadelphia. Cited by: endnote 21.
- Savoir scientifique et pouvoir social: L’École polytechnique, 1794–1914. Presses de la fondation nationale des sciences politiques, Paris. Cited by: §1, §1.
- Enquête Médico-psychologique sur la supériorité intellectuelle, II : H. Poincaré. Flammarion, Paris. link1 Cited by: §1, §1.
- Minkowski, mathematicians, and the mathematical theory of relativity. See The Expanding Worlds of General Relativity, Goenner et al., Einstein Studies, Vol. 7, pp. 45–86. link1 Cited by: endnote 20.
- A History of the Theories of Aether and Electricity, Volume 1: The Classical Theories. T. Nelson, London. Cited by: endnote 18.
Time-stamp: " 1.12.2023 21:44"