Henri Poincaré, theoretical physics, and relativity theory in
Paris.
Published in Karl-Heinz Schlote & Martina Schneider, eds,
Mathematics Meets Physics, Frankfurt am Main: Harri Deutsch,
2011, 213–239.
1 Introduction
In studies of the emergence of relativity theory, historians have sought to characterize the reception of relativist ideas with respect to national communities of physicists and mathematicians, in an effort to reveal underlying features of these communities, such as their openness to new ideas, and their capacity for change. Stimulating this activity are the basic publication counts, that tell us that the reception of relativity theory in academic journals varied markedly from one country to another. Periodicals based in Germany accounted for roughly half of all relativist publications before 1916, while Germany-based authors published two of every five articles on relativity during the same period, and made up two-fifths of the total number of scientists (one hundred) contributing to relativity theory. France, the fifth most active country from a quantitative point of view, accounted for seven percent of relativist articles, and counted eight relativist scientists, or about a twelfth of the total.11 1 Of 662 publications on relativity theory in periodicals between 1905 and 1916, 323 were published in Germany; see Walter (1996, Tables 4.3–4).
Examination of the content of these publications and their context of production allows for a finer-grained understanding of the differences revealed by quantitative analyses, and gives rise to theories of reception. For example, scholars of the reception of relativity theory in Germany and England have proposed explanatory models in which the details of post-secondary training in physics are seen as decisive.22 2 Pyenson 1987; Warwick 2003. Historians of French physics consider the muted reception of relativity in France as a consequence of a pervasive positivist outlook among French scientists, which would have favored the development of mathematics, while leaving little intellectual space for the distinct melange of experimental acumen, physical and mathematical reasoning that characterized the work of a Boltzmann, a Lorentz, or an Einstein.33 3 See Paty (1987, 115), Biezunski (1987, 184), and Pestre (1992, 117). On French isolationism in electrodynamics (and its exceptions), see Darrigol 2000, 352.
Attention to the conceptual foundations of early relativist publications reveals a marked difference in approach on the part of two contributors in particular: Henri Poincaré and Albert Einstein. Understanding this difference in approach has occupied historians and philosophers of science for over half a century, without reaching a consensus on its significance for the history of physics.44 4 A balanced overview of the “mystery of the Einstein-Poincaré connection” is provided by Darrigol (2004). Poincaré’s philosophical writings, published for the most part prior to the discovery of relativity, weigh heavily in these analyses, and according to one commentator, constituted an obstacle to the reception of Einstein’s theory of relativity in France until the 1920s.55 5 See Borella 2002. By the same token, Poincaré’s philosophical writings ought to have benefited his theory of relativity, but the above-mentioned publication counts indicate that they did not do so, either in France or elsewhere in the world.
The outlines of an alternative account of French contributions to relativity during the years from 1905 to 1912 are drawn in this paper. Poincaré’s intellectual and institutional leadership in French physics at the turn of the twentieth century is reviewed, and related to the emergence of Paul Langevin as his successor. Drawing on quantitative data and previously-unexploited manuscripts from Parisian archives, the paper compares the fate in France of Poincaré’s theory of relativity to that of the Einstein-Minkowski theory of relativity championed by Langevin, and links these events to Langevin’s rise to leadership of French theoretical physics.
2 Poincaré and theoretical physics in Paris
Compared to the situation of French physics in the first decades of the nineteenth century, in 1898 the future did not appear promising to Henri Poincaré. His pessimism stemmed from a perceived mismatch between the cognitive habits of the French scientist and the turbulent state of theoretical physics brought about by the discoveries of the past decade, including the null-result of the Michelson-Morley ether-drift experiment, the discovery of x-rays, the electron, the Zeeman effect, and radioactivity. A certain boldness was called for to explain such results, and Poincaré feared that the French were not up to the task at hand, as he expressed it in an official report to the Paris faculty of science:
The French mind, avid of clarity and logic, is repugnant of excessively temerarious adventures.
A new type of physicist was called for, according to Poincaré, in order to “discern the simplicity of laws beneath the complexity of phenomena”.66 6 Faculté des sciences de Paris, pièces annexes aux procès-verbaux, 1883–1903, 78–79, French National Archives. A transcription is available from the Henri Poincaré Papers website. The type of physicist Poincaré had in mind, although probably not the archetype, was Jean Perrin, whose candidacy he evaluated for a lectureship in physical chemistry on the Paris faculty of science. To some extent, Poincaré may have described here his own approach to the laws of physics, although his prowess in mathematics clearly set him apart from even the most mathematically-sophisticated of his colleagues in physics.
Paris did not yet dispose of a chair in theoretical physics per se, and would not create one until 1928, when the Rockefeller Foundation volunteered to finance a new institute.77 7 Siegmund-Schultze 2001. The first French chair nominally devoted to theoretical physics dates from 1894, when the faculty of science in Bordeaux hired Pierre Duhem. This is not to say that theoretical physics was neglected in Paris. At the Paris faculty of science, the chair of probability calculus and mathematical physics, dating from 1834, was devoted to the subject. Poincaré held this chair for a decade, from 1886 to 1896, and single-handedly brought French theoretical physics to international attention. The work in theoretical optics and fluid mechanics by his successor Joseph Boussinesq, however, found little echo outside of France.88 8 Darrigol 2005, 239.
For the sake of comparison, across the border, a modest institute for theoretical physics was created at the University of Berlin in 1889, at the behest of Hermann von Helmholtz, and by the turn of the century, such institutes had been created in Königsberg, Leipzig, Göttingen and Munich.99 9 Jungnickel & McCormmach 1986, vol. 2, 254. At the turn of the twentieth century, only two of these institutes were led by full professors: Max Planck in Berlin, and Woldemar Voigt in Göttingen.1010 10 Schlote 2004, 86. There were other outstanding theorists in Germany, notably Paul Drude, Willy Wien, and Arnold Sommerfeld, but some of these theorists felt Germany had lost its preeminence in the field since the time of Gustav Kirchhoff.1111 11 Jungnickel & McCormmach 1986, vol. 2, 159. Since the death of Heinrich Hertz in 1894, and Ludwig Boltzmann’s departure from Munich the same year, the brilliance of H. A. Lorentz in Leiden and Boltzmann in Vienna had cast shadows over their counterparts in Germany and France alike.
At least one theorist in Paris was prepared to meet the challenge posed by the recent results of experimental physics: Henri Poincaré. The fact that after 1896, Poincaré no longer occupied a chair of mathematical physics did not prevent him from lecturing and theorizing in this domain, just as earlier, he cultivated subjects of pure mathematics (function theory, algebraic topology), and celestial mechanics while nominally a professor of probability calculus and mathematical physics. Beginning in the late 1880s, Poincaré helped introduce Maxwell’s electromagnetic theory to French readers, and in the late 1890s, he exhibited a keen interest in Lorentz’s theory of electrons.1212 12 See Darrigol 2000. Interest in Lorentz’s theory grew rapidly when Lorentz used it to explain the splitting of Sodium D lines in an external magnetic field, an unexpected phenomenon discovered in 1896 by Lorentz’s former student, Pieter Zeeman (1865–1943). Poincaré communicated to the Paris Academy of Sciences a paper by Zeeman (1897) describing his discovery, and soon engaged with the explanation of the effect offered by Lorentz. Others in France soon took up studies of the Zeeman effect, including Alfred Cornu (1841–1902), Poincaré’s former physics professor at the École polytechnique, and Alfred Liénard (1869–1958), a former student of Poincaré’s, who taught mathematics and physics at the School of Mines in Saint-Étienne.
Poincaré’s engagement with electrodynamics was enduring, and remarkably innovative, featuring applications of sophisticated mathematical methods (complex analysis, group theory), and the reformulation of key concepts of Maxwell’s electromagnetic theory and Lorentz’s electron theory, along with applications of these methods and theories. For example, in the 1890s, Poincaré was among the first to use retarded potentials in Maxwell’s theory, and proposed the first electromagnetic theory of diffraction, which was soon extended by Arnold Sommerfeld. His demonstration of the recurrence theorem was recognized to have fundamental repercussions on physics, particularly for kinetic theory. He also provided a theory of multiple resonance for Hertzian oscillations, and the first exact solution of Maxwell’s equations for charged particles in a strong magnetic field.1313 13 Poincaré 1890, 1891b, 1891a, 1892a, 1897b.
By the turn of the century, Poincaré’s contributions to physics had won the admiration and respect of his peers across Europe and in the USA. Poincaré was one of only two Frenchmen invited to contribute to a volume in honor of G.G. Stokes in 1899, alongside Cornu.1414 14 See Cambridge Philosophical Society, ed. (1900). The next year, Poincaré was one of the three Frenchmen on the scientific committee of the international physics congress organized in Paris by the French Society of Physics, and presided by Cornu. One of ten vice-presidents of the physics congress, Poincaré presided the international congress of mathematicians, which conveniently took place in Paris the same week in August.1515 15 C.-E. Guillaume and L. Poincaré, eds. (1900). The following year, Poincaré was elected vice-president of the French Society of Physics, and in 1902, served as its president. A few years later, the Society made Poincaré one of its ten honorary members.1616 16 Three other French physicists had attained this status by 1909: Jules Violle, Gabriel Lippmann, and Émile-Hilaire Amagat; see Bulletin de la société française de physique (1908), p. 3*.
This recognition from Poincaré’s peers in physics did not mean that his authority in physics went uncontested, either at home or abroad. There were those, like the Scottish natural philosopher P. G. Tait, who found his lectures on mathematical physics to be excessively analytical, and unreliable on foundational issues.1717 17 See the review by P. G. Tait (1892) of Poincaré’s Thermodynamique (1892b), reedited with annotations (and Poincaré’s replies) in Walter et al., eds, eds (2007b, § 2-62). Near the end of the decade, when Lorentz explained the Zeeman effect on the basis of his theory of electrons, Poincaré proposed an alternative formula, which was mathematically sound, but for Lorentz, uncompelling from a physical standpoint.1818 18 Poincaré 1897a; Buchwald 1985, 226.
In France, Poincaré’s views on questions of mathematics or physics were very rarely challenged in public. The case of Marcel Brillouin (1854–1948) is instructive from this perspective. With doctoral degrees in mathematics and physics, Brillouin was named associate professor at the École normale supérieure in 1887. In the early 1890s, Brillouin dutifully pointed out what he thought was an error in the first edition of Poincaré’s lectures on Maxwell’s theory, concerning Hertzian waves. Poincaré’s gentle private lesson led Brillouin to retract his criticism.1919 19 See Poincaré’s correspondence with Brillouin in Walter et al., eds, 2007b, § 2-12; Brillouin 1891a, 1891b. In 1900, Brillouin replaced Joseph Bertrand as professor of general and mathematical physics at the Collège de France, and when a new edition of Poincaré’s Électricité et optique appeared in 1901, Brillouin had only high praise for it.2020 20 Poincaré 1901; Brillouin 1901.
At the turn of the century, Poincaré’s physical acumen was severely tested, when Gabriel Lippmann’s doctoral student, Victor Crémieu (1872–1935) published a result casting doubt on Rowland’s effect, whereby, in line with Maxwell’s theory, convected electricity produces a certain magnetic effect. Poincaré wrote the official report on Crémieu’s thesis, communicated several of his results to the Paris Academy of Sciences, and argued that if the result was confirmed, Maxwell’s theory would have to be abandoned. None of Europe’s leading physicists gave any credence to Crémieu’s findings, which if true, would have overturned the electron theories of Lorentz and Larmor, as well as Maxwell’s theory. In France, Brillouin shared Poincaré’s high opinion of Crémieu’s results, but Poincaré’s colleague at the Sorbonne, the physicist Henri Pellat (1850–1909) remained doubtful, as did Poincaré’s former teacher at the École polytechnique, Alfred Potier (1840–1905).
When Harold Pender, who was Rowland’s last doctoral student, confirmed Rowland’s effect in Baltimore, Poincaré saw to it that Pender and his equipment were transported to the Edmond Bouty’s laboratory in Paris, in order to perform experiments side-by-side with Crémieu. Pender emerged victorious from the encounter; to the French Society of Physics Pender explained not only how the Rowland effect manifested itself, but why Crémieu’s apparatus had failed to detect it.2121 21 Pender & Crémieu 1903. Historical accounts include Indorato & Masotto 1989, and Walter et al., eds. 2007b, § 2-17. The result of the encounter suggests that Poincaré had misjudged the situation; nonetheless, he obtained what he required as a theoretical physicist: an experimental decision between Maxwellian and non-Maxwellian electrodynamics.
Pender and Crémieu’s account of their parallel investigations of convected electricity appeared in a leading journal of French physics: the Journal de physique théorique et appliquée (JPTA), founded in 1872. During the first decade of the twentieth century, the JPTA’s editorial board counted two professors of physics from the Paris faculty of science, Edmond Bouty and Gabriel Lippmann, along with a pair of senior theorists, Alfred Potier and Élie Mascart, neither of whom survived the decade. Filling out the editorial board were a trio of associate editors, former students of the École normale supérieure: Lucien Poincaré, Bernard Brunhes, and Georges Sagnac; and one non-Normalien associate editor, Marcel Lamotte, an associate professor of physics at Clermont-Ferrand, who like Brunhes had helped edit Poincaré’s volumes on mathematical physics in the early 1890s.
The JPTA did not publish contributions in theoretical physics that involved sophisticated mathematical elaboration, in order to remain accessible to “isolated” physicists, which is to say, those out of range of science faculties and their libraries.2222 22 This was the policy announced by the JPTA’s founder, J.-C. Almeida, in the first issue of the review. This approach manifested itself in the selection of articles for publication, and in the abstracts of articles published abroad. More often than not, when an article featured a mathematical argument, the JPTA abstract revealed this fact alone, with no judgment of merit or meaning. Consequently, readers were ill-informed of current work in theoretical physics, beyond what might be guessed from reading the name of the author, and the title of the contribution.
There were other venues in France for publishing research in theoretical physics, including the Annales de chimie et de physique (or ACP for short), Le Radium, the Annales scientifiques de l’École normale supérieure, and the Journal de mathématiques pures et appliquées. The latter two journals attracted few papers on physics, unlike Le Radium, founded in 1904 by H. Becquerel, P. Curie, E. Rutherford, Ch.-E. Guillaume and others. Le Radium effectively competed for readers with the JPTA, providing translations of German and French contributions, and abstracts of various periodicals, until the two journals fused in 1920. The ACP, founded in 1816, attracted significant communications in the first decade of the twentieth century from Paul Langevin, Jacques Hadamard, Marcel Brillouin, and the latter’s student, Jean Perrin. At the beginning of the decade, the ACP was directed by the venerable trio of Marcelin Berthelot, Élie Mascart, and Henri Moissan, none of whom were still alive in 1910. At the end of the first decade, a different trio of editors directed the ACP: the chemist Albin Haller (1849–1925) and his two colleagues on the Paris faculty of science, Lippmann and Bouty, who continued to edit the JPTA.
During this period the ACP published doctoral theses in physics, as well as extended summaries of experimental and theoretical investigations. Two examples may be mentioned here. One of these is the Swiss theorist Walter Ritz’s long memoir, “Critical investigations in general electrodynamics”, in which Ritz gave an overview of the work of Lorentz, Poincaré, Einstein, and others, and sketched an alternative approach to the electrodynamics of moving bodies, based on retarded potentials and a principle of superposition.2323 23 Ritz 1908; Martínez 2004. Another is Perrin’s “Brownian motion and molecular reality”, where he presented the results of experiments that confirmed Einstein’s formula for Brownian motion of a particle in a fluid, work for which Perrin was awarded the Nobel Prize in physics in 1926.2424 24 Perrin 1909; Nye 1972.
The only other publishing outlet for research in theoretical physics in France, but one more widely cited than the ACP or any other French scientific journal, was the organ of the Paris Academy of Sciences, the Comptes rendus hebdomadaires (hereafter CRAS). This was where Poincaré published most often, averaging nine papers a year throughout his career, including a signal contribution to relativity theory on 6 June 1905. The CRAS enforced a page limit on its contributors, and Poincaré’s four-page summary was no exception to the rule. The memoir summarized in the CRAS appeared in the Rendiconti del Circolo matematico di Palermo, a journal in which since 1888 Poincaré had published on the theory of differential equations, analytical mechanics, and algebraic topology. Until 1906, Poincaré published all his articles on physics (excluding notes in the CRAS) either in foreign journals, or in a Paris-based journal of electrical engineering, Éclairage électrique, on the editorial board of which he served beginning in 1899.
One consequence of this habit was that until 1906, Poincaré’s latest research in theoretical and applied physics was known best to French electrical engineers, and readers of CRAS and foreign research journals. Students of physics knew Poincaré best through his lectures on mathematical physics, published in thirteen volumes (not counting translations to German, or reeditions). The effect of these volumes was described somewhat breathlessly by the mathematician (and former Poincaré student) Maurice d’Ocagne, for whom Poincaré had, in addition to being the world’s premier theoretical astronomer,
…carved for himself an unequaled position as a theoretical physicist, projecting a new light, emanating from the most unexpected sources, upon every part of mathematical physics: heat, optics, electricity, elasticity, capillarity, etc. …. He has covered everything, renewed everything, extended everything. […]
What is more, there are many experimentalists who make no mistake in recognizing all they owe to the theoretical views introduced to science by Mr. Poincaré, and who have quite often reoriented their laboratory investigations to the great benefit of the general advance of our knowledge. (Maurice d’Ocagne 1909, 541)
What d’Ocagne’s remark suggests most clearly is the source of Poincaré’s preeminence in French theoretical physics, and his influence on research agendas in experimental physics. Physicists who acknowledged such an influence included, among others in France, Henri Becquerel, René Blondlot, Gustave Le Bon, Paul Langevin, Georges Sagnac, Alfred Perot, and Victor Crémieu; in Geneva, Lucien de la Rive and Édouard Sarasin; in Kristiania (now Oslo), Kristian Birkeland.2525 25 Poincaré’s interaction with experimental physicists is well-documented in his correspondence; see the introduction to Walter et al., eds, 2007b.
While Poincaré’s influence on the agenda of experimentalists is apparent, what can be said of his mark on the agenda of theorists? Some of the aforementioned experimentalists also wore a theorist’s cap on occasion, like Birkeland, Langevin, and Sagnac. All three of these physicists published on subjects stemming from those taken up earlier by Poincaré, notably in the domains of Hertzian waves and electron theory; all were former students of Poincaré. According to another former student of Poincaré’s, Arthur Korn, there was not a single physicist anywhere whose work had not found fundamental stimulation in Poincaré’s lectures.2626 26 Korn 1912.
Poincaré is often characterized by historians as a leading critic of theories of physics, and indeed, his lectures in mathematical physics offered a magisterial discussion of rival theories in the several branches of physics, that compared relative strengths and weaknesses.2727 27 Such a characterization is offered by Darrigol 1995, 2000. His lectures on Maxwell’s theory were eagerly read in Germany (in German translation), and exercised a profound influence on the first German textbooks on Maxwellian electrodynamics.2828 28 See Darrigol 1993; 2000, 354. Some of his non-technical analyses were reedited for a larger audience in the four anthologies of his epistemological writings on mathematics and the exact sciences edited by 1913, which were widely read and appreciated by both specialists and the general reading public alike.2929 29 According to Lebon (1912, 84), the first of these anthologies, entitles La science et l’hypothèse (1902), sold twenty thousand copies by 1911. On the composition of Poincaré’s anthologies, see Rollet (2001, chap. 4). Poincaré’s critical acumen in theoretical physics was appreciated by his peers, including Joseph Larmor, who contributed a preface to the English translation of the first of the anthologies: Science and Hypothesis.
On an international level, with the discovery of x-rays, the electron and radioactivity in the closing years of the nineteenth century, the physics of charged particles filled the pages of physics journals. French prowess in experimental microphysics received international recognition following work by Henri Becquerel and the Curies on radioactive matter, and René Blondlot on electrical convection, although the latter’s reputation was later tarnished when what he called “N-rays” proved spurious. On the theoretical side, Poincaré and Alfred Liénard were among the first theorists to contribute to Lorentz’s electron theory, and to apply it to dispersion phenomena and the Zeeman effect.3030 30 See Buchwald 1985. Outside of France, respected theorists at the turn of the twentieth century included, first and foremost, Lorentz in Leiden, Boltzmann in Vienna, Joseph Larmor and J.J. Thomson in Cambridge, Ernest Rutherford in Montreal, Paul Drude in Giessen, Max Planck in Berlin, Sommerfeld in Aachen, Wilhelm Wien in Würzburg, Woldemar Voigt, Emil Wiechert, Max Abraham, and Walther Nernst in Göttingen.
Critical analysis of physical theories was an activity at which Poincaré was skilled and accomplished, and for which he was amply rewarded. His contributions to physics, however, went well beyond writing textbooks and critiques of others’ work, into the creative realm of theory construction. Among the theoretical physicists mentioned above, Sommerfeld and Abraham found significant inspiration in Poincaré’s theories of physics. Sommerfeld’s electromagnetic theory of diffraction of plane waves (1896) improved on Poincaré’s groundbreaking paper of 1892, while Abraham borrowed on the Frenchman’s conception of electromagnetic momentum to form his theory of electron dynamics.3131 31 Poincaré 1892a; Sommerfeld 1896, 2004. On Abraham’s and Planck’s theories see Miller 1980, 1981. Last but not least, in the summer of 1907, Hermann Minkowski took up the elements of Poincaré’s four-dimensional approach to relativity theory, in what became a game-changing theory of physics: the theory of spacetime.3232 32 Poincaré 1906; Minkowski 1908; Walter 2007a, 2008.
The latter three contributions were among those cited in support of an ultimately unsuccessful campaign to award Poincaré the Nobel prize in physics in 1910, in addition to work on the propagation of Hertzian waves, and the theories of vibrating plates, rotating fluid masses, and electron stability. The failure of Poincaré’s Nobel campaign reflects in part the still-uncertain status of the theory of relativity in 1910, and in fact, the Nobel committee never awarded a prize in recognition of the discovery of special relativity. In context, it is curious that a Nobel prize nomination emanating from the Paris Academy of Sciences in January 1910, and including among its signatories the Academy’s permanent secretary for the mathematical sciences, Gaston Darboux, should feature work “of the highest importance” by Poincaré on the principle of relativity.3333 33 See Darboux et al. to the Nobel Committee, ca. 1 January 1910, transcribed and annotated in Walter et al., eds, 2007b, § 2-62. On the organization of the 1910 campaign, see Ph. Nabonnand’s notes to the correspondence between Poincaré and G. Mittag-Leffler (Nabonnand 1999). On 5 June 1905, Poincaré’s precis of relativity theory appeared in the Comptes rendus of the Academy, announcing a longer work published in the Palermo Rendiconti.3434 34 Poincaré 1905, 1906. Afterwards, no notes were published by anyone on this subject in the Comptes rendus until 7 February 1910, when results of cathode-ray deflection experiments by Charles-Eugène Guye and Simon Ratnowsky in Geneva appeared, tending to confirm Lorentz’s predictions of velocity-dependent mass.3535 35 Guye and Ratnowsky (1910), originally submitted on 10 January 1910, and withdrawn by Guye, ostensibly to permit the inclusion of new data (Guye to Gaston Darboux, 30 January 1910, Archives of the Academy of Sciences, session folder, 7 February 1910). Contrary to Darboux’s description, the publication record suggests that the theory of relativity was of little importance to French science, at least until February 1910.
What happened to the theory of relativity in France during the latter half of the first decade of the twentieth century? And how did Einstein’s theory come to prominence in France in 1911? In the next section, I show that while Lorentz’s theory was often discussed, alternative theories remained nearly invisible in France until 1911. The situation changed in 1911, as the final section will show.
3 The invisibility of Einstein’s theory in France
In the scientific centers of Western Europe, physicists did not distinguish at first the theories of Lorentz, Poincaré, and Einstein. Of these three founders of relativity theory, Poincaré alone took care to identify the differences between his theory and that of Lorentz; Einstein’s theory had not yet been published when he wrote his memoir. A year later, after Einstein’s theory had been aired in the Annalen der Physik, Poincaré took care to explain to his students at the Sorbonne how his theory of relativity differed from that of Einstein, albeit without ever mentioning Einstein or his theory.
Poincaré performed a curious thought experiment for his students, in which a pair of inertial observers, one at rest, the other moving away in a straight line at constant speed, describe the form of a locus of light at a certain instant of time. An observer at rest with respect to the ether judges the light locus to have the form of a sphere, the radius of which increases with the speed of light. Observers in motion with respect to the ether, Poincaré explained, would conclude that the light locus at any instant of time (as determined via co-moving light-synchronized clocks) is represented by an ellipsoid of rotation, elongated in the direction of observer motion with respect to the ether. In Einstein’s theory, by contrast, the light locus at any given instant of time (as determined via co-moving light-synchronized clocks) is always represented by a sphere.3636 36 See my forthcoming paper in Einstein Studies. For alternative explanations of Poincaré’s light-ellipsoid, see Cuvaj (1970, 74) and Darrigol (2006, 17–19). After presenting his view of relativity to his students, Poincaré published his light-ellipsoid theory of relativity in France’s leading popular-science biweekly, the Revue générale des sciences pures et appliquées. He did not mention Einstein’s theory, and in the Revue générale no one else did, either, until Maurice Lémeray wrote of “Einstein’s beautiful results” four years later.3737 37 Poincaré 1908; Lémeray 1912.
Poincaré’s silence with respect to Einstein’s theory has been the subject of much historical speculation, and will not concern us here. Instead, let us ask why no one else in France saw fit to mention Einstein’s theory in print before 1911. And to begin with, let us investigate why one person in particular, Paul Langevin, did not mention Einstein’s theory in print before 1911. Recall that in 1905 Langevin proposed an electron theory similar in some respects to that of Alfred Heinrich Bucherer, featuring an electron model of constant volume, and velocity-dependent shape, and that Poincaré showed Langevin’s theory to be incompatible with relativity. Langevin acknowledged Poincaré’s judgment of his theory, but did not give it up until the experimental results presented by A.H. Bucherer in September 1908 persuaded him to do so.3838 38 See Langevin’s Notice sur les travaux scientifiques (1908, 35). To put it briefly, until the fall of 1908 there were several plausible alternatives available to relativity theory, some of which enjoyed, like Abraham’s rigid-electron theory, better empirical support in some tests than did the theory of relativity.3939 39 On the choice between alternative theories of the electrodynamics of moving bodies circa 1905, see Darrigol (2000, 391).
Einstein was not unknown in French physics circles, and his name was cited in contexts other than relativity in the period from 1905 to 1910. In kinetic theory, for example, Einstein’s formula of 1905 for specific heat was promoted by Jean Perrin in 1908, and referred to simply as “Einstein’s formula”. A look at the abstracts published by the JPTA from 1905 to 1911 reveals that the “Abraham theory” of the electrodynamics of moving bodies was mentioned twice, the “Einstein theory” three times, and the “Poincaré theory” or “Lorentz-Poincaré theory” four times. One notices that Poincaré’s theory never stood alone in these abstracts, but was always accompanied by a reference to Lorentz’s theory, which was mentioned much more often than any other, garnering a total of twenty-two independent occurrences.
Also, the paucity of detail in JPTA abstracts on relativity and electron theory, compared with that provided for other subjects, suggests a certain lack of comprehension or interest on the part of the abstract writer. A general ignorance of and disinterest in relativity theory was not unique to French physicists, as even in Germany, publication numbers remained modest in this area until 1909, when they began to climb rapidly (see Fig. 2). One difficulty for relativity theory was its poor performance in electron-deflection experiments, which led many to believe that relativity theory was empirically untenable. In a discussion of electron theory in 1906, for example, Paul Ehrenfest considered Lorentz’s theory to have been definitively disproved by experiment, and Ehrenfest’s opinion was duly related by Léon Bloch for readers of Le Radium.4040 40 Ehrenfest 1906; Le Radium 3, 1906, p. 148. In such circumstances, it is a wonder that any physicist bothered learning relativity theory before the end of 1908.
After an experimental confirmation of relativity theory was announced in September 1908, the incentive to learn the theory, and to investigate its consequences naturally increased. What is curious in the French context is that apart from Poincaré, no other physicist took up relativity, until Paul Langevin lectured on the subject at the Collège de France in 1910–1911. According to Poincaré’s own report, he pursued a relativistic theory of elastic collisions, but deemed his results unworthy of publication. As he explained it to a Berlin audience in late 1910, the lack of such a theory was one reason why the new mechanics of relativity could not be considered “definitively grounded”.4141 41 Poincaré 1910, 115–116. In front of French audiences, Poincaré offered a different message, designed to reassure those worried about overturning Newtonian mechanics: the “old mechanics”, Poincaré announced, was still the one for “our practical life and our terrestrial technology”.4242 42 “Quoi qu’il en soit, d’ailleurs, elle restera la mécanique des vitesses très petites par rapport à la vitesse de la lumière, la mécanique donc de notre vie pratique et de notre technique terrestre.” Plenary lecture, 3 August, 1909, to the meeting of the French Association for the Advancement of Science in Lille (Poincaré 1909).
Poincaré’s measured consideration of the theory he helped create may have dissuaded a few junior French theorists from following in his tracks, but not Paul Langevin.4343 43 On Langevin’s relation to Poincaré and Einstein, see Paty (2002). As a student of Poincaré’s 1896 lectures on the elastic theory of light, Langevin had learned how a certain theorist referred to as “Somerset” extended Poincaré’s theory of polarization by diffraction.4444 44 Fonds Langevin, Notebook “Poincaré Élasticité et optique III 1896”, carton 123, Bibliothèque de l’École supérieure de physique et de chimie industrielle, Paris. In a later appreciation of Poincaré’s contributions to physics, Langevin recalled Poincaré’s lectures on optics, which showed how Sommerfeld “brilliantly followed a path” opened by Kirchhoff and Poincaré via complex analysis; see Langevin (1913, 691). Ten years later, on the strength of this work, and more recent contributions to electron theory, this same theorist – better known as Arnold Sommerfeld – was named to the chair of theoretical physics in Munich, formerly held by Boltzmann.4545 45 Eckert 1984. Sommerfeld was in charge of the physics volume of Felix Klein’s planned six-volume Encyclopedia of Mathematical Sciences with Applications, the first entries of which appeared in 1903.4646 46 See Eckert and Märker, eds, 2001, vol. 1, p. 40. On 16 April, 1906, Sommerfeld informed Langevin that Klein had agreed to let him co-edit the French version of the physics volume with Jean Perrin, a task that would occupy the two Frenchmen for nearly a decade.4747 47 Fonds Langevin, op. cit., carton 76. Along with their editing duties, Sommerfeld and Langevin shared for several years the electromagnetic world-view, which promised a unification of all forces on an electromagnetic basis. But as mentioned above, in late 1908, theory and experiment conspired to convince Langevin of the cogency of the theory of relativity.
As a former student of Poincaré’s, and an occasional dinner guest at his flat in Paris, Langevin would have been at first glance a natural candidate to take up Poincaré’s theory of relativity. A similar remark may be made about Sommerfeld, who did not hear Poincaré’s lectures at the Sorbonne, but who admired and emulated his approach to physics. Whatever affinity Sommerfeld and Langevin had with Poincaré and his science, they both preferred the Einstein-Minkowski theory to that of Poincaré. For Sommerfeld, it was Minkowski’s spacetime theory that persuaded him of the cogency of relativity theory.4848 48 Walter 1999, 70. Langevin, too, was impressed by Minkowski’s theory, and by Sommerfeld’s related four-dimensional vector algebra and analysis, which he presented in his 1910–1911 lectures at the Collège de France.4949 49 Sommerfeld 1910a, 1910b. Likewise, Minkowski admired Langevin’s contributions to the kinetic theory of gases; see Minkowski to Felix Klein, 1 Oct. 1906, Klein Nachlass, Niedersächsische Staats- und Universitätsbibliothek. The elements of spacetime theory were readily available to French readers by then, since in late 1909, a pair of former students of the École normale supérieure had translated Minkowski’s 1908 lecture “Space and time” for publication in the Annales scientifiques de l’École normale supérieure.5050 50 Minkowski (1909), translated from the German original by Aimé Hennequin and Joseph Marty. On Poincaré’s response to Minkowski’s theory, see Walter (2009).
Like Poincaré, Langevin felt that the ether was not a wholly superfluous concept for modern physics. One auditor of Langevin’s lectures, Léon Brillouin, recorded Langevin’s remark on this subject:
The very notion of the ether loses its sense, says Einstein – this is an exaggeration. We can’t discern our speed with respect to the ether, but we can discern [our] accelerations and rotations.5151 51 “La notion même d’éther perd son sens, dit Einstein–c’est exagéré. On ne peut saisir notre vitesse p[ar] rapp[ort] à l’éther, mais on peut saisir les accélérations et rotations.” Léon Brillouin, Notebook “Cours de Relativité au Collège de France 1910–1911”, Léon Brillouin Papers, Box 7, folder 8, American Institute of Physics, Niels Bohr Library. Langevin made the same point – without mentioning Einstein by name – in a lecture delivered on 10 April 1911 to the Fourth International Congress of Philosophy in Bologna, where Poincaré was present; see Langevin (1911, 233).
On the subject of light-waves, Langevin maintained on another occasion that a spherical light-wave in one inertial frame is actually spherical for all inertial observers.5252 52 Langevin 1912, 335. The latter view signals Langevin’s break with Poincaré, for whom the light locus only appeared spherical for observers in motion with respect to the ether. In fact, Langevin fully agreed with Einstein and Minkowski that the universal validity of the principle of relativity implied a new view of space and time, and he defended this view publicly, beginning in 1911.
To put Langevin’s defense of Einstein-Minkowski theory into historical perspective, let us examine some publication numbers. In 1911, publication of articles on relativity theory in periodicals worldwide hit a peak at one hundred and seventeen titles, after a sustained increase in scientific interest beginning in 1909 (see Fig. 1). This increase is reflected on a modest scale, and with a delay of a year or two, in the United Kingdom and in France. Figure 2 shows the evolution of publication numbers from 1905 to 1916 for the top five nations in article productivity. French numbers rose slightly in 1911, and peaked at thirteen articles in 1913.5353 53 These publication numbers do not take into account an author’s nationality or workplace. Data correlating the production of articles on relativity to nationality of the writer is presented in Walter (1996), which is also the source of the data in the figures presented here, augmented by fifty titles gleaned from the author’s subsequent research. The publication database is freely available from the author’s homepage.
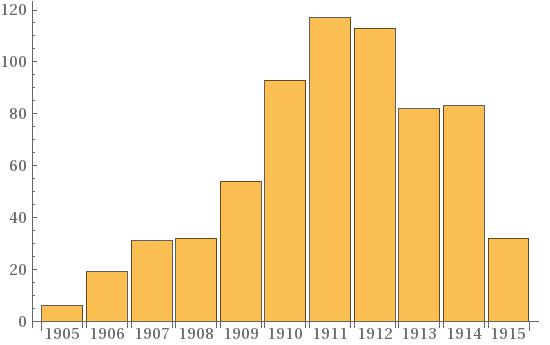
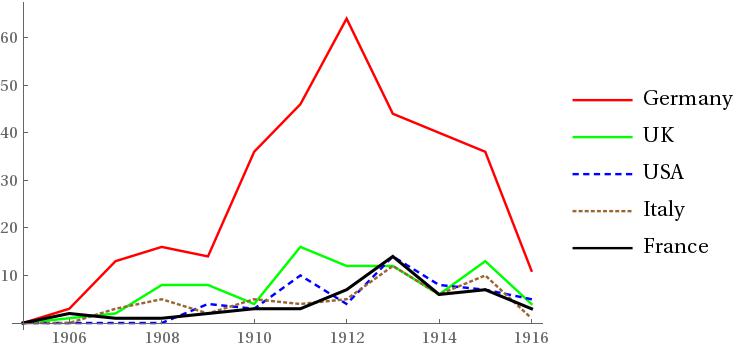
Bare publication numbers tell us nothing of the causes of their annual fluctuation, a fact which leads us back to the JPTA abstracts. In 1911, “Einstein theory” is mentioned in nine abstracts, six of which mention no other theory. Next comes “Lorentz theory”, with five mentions, followed by one mention each for Poincaré and Minkowski. The novelty in 1911 French physics, according to this source, was Einstein’s theory of relativity. A closer look at the JPTA abstracts, however, suggests that these citation figures be treated with prudence. In 1911, the JPTA recruited a new abstract writer, a nautical engineer from Antibes, Maurice Lémeray (b. 1860), and assigned him articles on relativity published in German or English. A science teacher turned warship designer, Lémeray was himself a prolific writer on relativity, having published more articles in 1911 and 1912 than any other Frenchman. His writings show no marked allegiance to either Einstein or Poincaré, but agree in general with Einstein’s theory. Indeed, Lémeray was the first to cite Einstein’s publications on relativity in the Comptes rendus, in a note communicated to Academy of Sciences by Poincaré, whose name Lémeray was careful to cite.5454 54 Lémeray 1911. In summary, the increased number of citations of Einstein’s theory in the 1911 JPTA abstracts has more to do with staff changes at the JPTA than with any bound in recognition of Einstein’s contributions to relativity among French physicists.
The details of Lémeray’s rise to prominence in France throw light on the reception of Einstein’s theory. Archival documents reveal that Lémeray sought the Paris Academy’s approval for his work on relativity as early as September 1910, when he submitted a manuscript to Gaston Darboux, one of the Academy’s permanent secretaries.5555 55 Session folder, 3 October 1910, Archives of the Academy of Sciences, Paris. Judged unfit for publication, the four-page note entitled “On the Lorentz transformation” purported to demonstrate Lorentz’s formulas for local time, length contraction, and transverse and longitudinal mass from Einstein’s twin postulates of relativity and universal lightspeed invariance, and dimensional analysis. Lémeray insisted that his results were free of “any hypothesis on the mechanism of phenomena or on any electrical theory”, and he cited only one paper: Einstein’s first French-language publication on relativity in the Archives de Genève. His purported demonstration of time dilation from the longitudinal Doppler effect for lightwaves, however, involved circular reasoning, and probably rendered his manuscript unpublishable. What this episode suggests is that the invisibility of Einstein’s theory in France until 1911 was due in part to the paucity of physicists prepared to meet the cognitive challenge of Einstein’s theory, combined with the existence of a rigorous manuscript review process. Similar instances of manuscript rejection in this area of physics took place elsewhere, of course, Germany included.5656 56 See, for example, Lewis Pyenson’s review (1985, chap. 8) of Max Planck’s rejection of papers submitted to the Annalen der Physik.
4 Epilogue
With assistance from Perrin, Langevin, and Lémeray, Einstein’s star was ascending over France by 1911. In November, 1911, Poincaré recommended him for a chair in theoretical physics at the ETH in Zurich, commenting that “the future will show more and more what Mr. Einstein’s value is”, and in January 1912, Einstein was named to this chair, and elected a non-resident council member of the French Society of Physics.5757 57 Poincaré to Pierre Weiss, ca. November, 1911, transcribed in Walter et al., eds, 2007b, § 2-59-3; Procès-verbaux de la Société française de physique 1912, p. 9. In May, 1912, Poincaré admitted that the new mechanics of relativity could serve as a basis for a redefinition of time and space, thereby recognizing the philosophical significance of Einstein-Minkowski theory.5858 58 Poincaré 1912; Walter 2009. This was a giant step for Poincaré, but it came too late to make any difference for physics in France. By 1912, the leading French theorists, including Langevin, and the mathematicians Émile Borel and Élie Cartan, had already adopted Einstein-Minkowski theory.5959 59 See Borel’s 1913 lectures on Minkowski spacetime at the Sorbonne (Borel 1914), and Cartan’s lecture on the “new kinematics” of relativity before the French Society of Mathematics (Cartan 1912).
The engagement of Borel, Cartan, and other French mathematicians with the theory of relativity followed an example set in Germany by Minkowski, Gustav Herglotz, and Felix Klein. To some extent, the contributions of French mathematicians compensated the feeble participation of French theoretical physicists – Poincaré excepted – in the construction and diffusion of relativity. Once again, Langevin appears to have been instrumental in attracting the attention of French mathematicians to the study of Einstein-Minkowski theory. His role in introducing Einstein’s theory to French scientists was later described by Jacques Hadamard as follows:
It is well known that, under the powerful leadership of Mr. Langevin, the young French physicists rallied to the new movement of ideas created by Mr. Einstein’s discoveries. But cooperation with this movement was no less important to mathematicians, whose doctrines the new theory brought into play to a higher degree than any other previous physical conception. This is just what geometers like Mr. Borel understood from the beginning. (Hadamard 1922, i)
What Hadamard’s remark suggests is that for us to understand the reception of relativity in France, we need to go beyond the small circle of theoretical physicists, and examine how mathematicians came to engage with the theory.
In this essay, Poincaré’s influence on theoretical physicists in France has been discussed, but not his interaction with mathematicians. Nonetheless, even in the restricted domain of theoretical physics in France, the interactions between mathematics and physics appear decisive for the reception of relativity theory. The systematic appeal to sophisticated and powerful mathematics in the construction and elaboration of physical theory was a legacy Poincaré bestowed on all his physics students. In this sense, Poincaré may be said to have smoothed the path in France for both Paul Langevin and the Einstein-Minkowski theory of relativity, at the expense of his own approach to relativity.
References
- Einstein’s reception in Paris in 1922. See The Comparative Reception of Relativity, Glick, pp. 169–188. Cited by: footnote 3.
- Introduction géométrique à quelques théories physiques. Gauthier-Villars, Paris. External Links: Link Cited by: footnote 59.
- Les écrits épistémologiques de Poincaré, obstacles à la diffusion de la relativité. Revue d’histoire des sciences 55 (1), pp. 45–81. External Links: Link Cited by: footnote 5.
- Compte rendu : H. Poincaré, Électricité et optique II. Revue générale des sciences pures et appliquées 2, pp. 268. External Links: Link Cited by: footnote 19.
- Compte rendu et analyse : Henri Poincaré, Électricité et optique. Bulletin des sciences mathématiques 15, pp. 129–146. External Links: Link Cited by: footnote 19.
- Compte rendu et analyse : Henri Poincaré, Électricité et optique. Bulletin des sciences mathématiques 25, pp. 118–127. External Links: Link Cited by: footnote 20.
- From Maxwell to Microphysics. University of Chicago Press, Chicago. Cited by: footnote 18, footnote 30.
- Memoirs Presented to the Cambridge Philosophical Society on the Occasion of the Jubilee of Sir George Gabriel Stokes. Cambridge University Press, Cambridge. External Links: Link Cited by: footnote 14.
- Sur les groupes de transformations de contact et la cinématique nouvelle. Société mathématique de France, comptes rendus des séances, pp. 23. Cited by: footnote 59.
- A History of Relativity: The Role of Henri Poincaré and Paul Langevin. Ph.D. Thesis, Yeshiva University, New York. Cited by: footnote 36.
- Einstein, 1905–2005. Birkhäuser, Basel. Cited by: O. Darrigol (2006).
- The electrodynamic revolution in Germany as documented by early German expositions of ‘Maxwell’s theory’. Archive for History of Exact Sciences 45, pp. 189–280. Cited by: footnote 28.
- Henri Poincaré’s criticism of fin de siècle electrodynamics. Studies in History and Philosophy of Modern Physics 26, pp. 1–44. Cited by: footnote 27.
- Electrodynamics from Ampère to Einstein. Oxford University Press, Oxford. Cited by: footnote 12, footnote 27, footnote 28, footnote 3, footnote 39.
- The mystery of the Einstein-Poincaré connection. Isis 95 (4), pp. 614–626. Cited by: footnote 4.
- Worlds of Flow: A History of Hydrodynamics from the Bernoullis to Prandtl. Oxford University Press, Oxford. Cited by: footnote 8.
- The genesis of the theory of relativity. See Einstein, 1905–2005, Damour et al., Progress in Mathematical Physics, Vol. 47, pp. 1–32. Cited by: footnote 36.
- Arnold Sommerfeld: Wissenschaftlicher Briefwechsel. GNT-Verlag, Diepholz. Cited by: footnote 46.
- Boltzmann, Sommerfeld und die Berufungen auf die Lehrstühle für theoretische Physik in Wien und München 1890–1917. Mitteilungen der Österreichischen Gesellschaft für Geschichte der Naturwissenschaften 4, pp. 101–119. Cited by: footnote 45.
- Zur Stabilitätsfrage bei den Bucherer-Langevin-Elektronen. Physikalische Zeitschrift 7, pp. 302–303. Cited by: footnote 40.
- The Comparative Reception of Relativity. Reidel, Dordrecht. Cited by: M. Biezunski (1987), M. Paty (1987), L. Pyenson (1987).
- The Expanding Worlds of General Relativity. Birkhäuser, Boston/Basel. Cited by: S. A. Walter (1999).
- Rapports présentés au congrès international de physique. Gauthier-Villars, Paris. External Links: Link Cited by: footnote 15.
- Sur la variation de l’inertie de l’électron en fonction de la vitesse dans les rayons cathodiques et sur le principe de relativité. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 150 (6), pp. 326–329. Cited by: footnote 35.
- Préface. See Introduction au calcul tensoriel et au calcul différentiel absolu, Juvet, pp. i–ii. Cited by: §4.
- The Significance of the Hypothetical in the Natural Sciences. Walter de Gruyter, Berlin. Cited by: S. A. Walter (2009).
- Poincaré’s role in the Crémieu-Pender controversy over electric convection. Annals of Science 46 (2), pp. 117–163. External Links: Link Cited by: footnote 21.
- Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein. University of Chicago Press, Chicago. Cited by: footnote 11, footnote 9.
- Introduction au calcul tensoriel et au calcul différentiel absolu. Blanchard, Paris. Cited by: J. Hadamard (1922).
- Henri Poincaré (1854–1912). Sitzungsberichte der Berliner mathematischen Gesellschaft 12, pp. 3–13. Cited by: footnote 26.
- Notice sur les Travaux Scientifiques. n.p., Paris. Cited by: footnote 38.
- L’évolution de l’espace et du temps. Scientia (Rivista di Scienza) 10 (29), pp. 31–54. External Links: Link Cited by: footnote 51.
- Le temps, l’espace et la causalité dans la physique moderne. Bulletin de la Société française de philosophie 12, pp. 1–28. Cited by: footnote 52.
- L’œuvre d’Henri Poincaré : le physicien. Revue de métaphysique et de morale 21, pp. 675–718. External Links: Link Cited by: footnote 44.
- Henri Poincaré : Biographie, bibliographie analytique des écrits. Gauthier-Villars, Paris. External Links: Link Cited by: footnote 29.
- Le principe de relativité et les forces qui s’exercent entre les corps en mouvement. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 152 (22), pp. 1465–1468. Cited by: footnote 54.
- Le principe de relativité et la mécanique. Revue générale des sciences pures et appliquées 23 (5), pp. 174–183. Cited by: footnote 37.
- Ritz, Einstein, and the emission hypothesis. Physics in Perspective 6, pp. 4–28. Cited by: footnote 23.
- On some other approaches to electrodynamics in 1905. See Some Strangeness in the Proportion, Woolf, pp. 66–91. Cited by: footnote 31.
- Albert Einstein’s Special Theory of Relativity: Emergence (1905) and Early Interpretation. Addison-Wesley, Reading, MA. Cited by: footnote 31.
- Die Grundgleichungen für die electromagnetischen Vorgänge in bewegten Körpern. Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, pp. 53–111. External Links: Link Cited by: footnote 32.
- Espace et temps. Annales scientifiques de l’École normale supérieure 26, pp. 499–517. Cited by: footnote 50.
- La correspondance d’Henri Poincaré, Volume 1: La correspondance entre Henri Poincaré et Gösta Mittag-Leffler. Birkhäuser, Basel. External Links: Link Cited by: footnote 33.
- Molecular Reality: A Perspective on the Scientific Work of Jean Perrin. Elsevier, Amsterdam. Cited by: footnote 24.
- Biographie du conférencier M. Henri Poincaré. Journal de l’Université des Annales 3, pp. 539–541. Cited by: §2.
- The scientific reception of relativity in France. See The Comparative Reception of Relativity, Glick, pp. 113–167. Cited by: footnote 3.
- Poincaré, Langevin et Einstein. Épistémologiques 2, pp. 33–73. Cited by: footnote 43.
- Recherches contradictoires sur l’effet magnétique de la convection électrique. Bulletin des séances de la Société française de physique, pp. 136–162. Cited by: footnote 21.
- Mouvement brownien et réalité moléculaire. Annales de chimie et de physique 18, pp. 1–114. Cited by: footnote 24.
- Physique et physiciens en France 1918–1940. Éditions des archives contemporaines, Paris. Cited by: footnote 3.
- Sur le problème des trois corps et les équations de la dynamique. Acta mathematica 13, pp. 1–270. External Links: Link Cited by: footnote 13.
- Sur la résonance multiple des oscillations hertziennes. Archives des sciences physiques et naturelles 25, pp. 609–627. External Links: Link Cited by: footnote 13.
- Sur la théorie des oscillations hertziennes. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 113, pp. 515–519. External Links: Link Cited by: footnote 13.
- Sur la polarisation par diffraction. Acta mathematica 16, pp. 297–339. External Links: Link Cited by: footnote 13, footnote 31.
- Thermodynamique. Georges Carré, Paris. External Links: Link Cited by: footnote 17.
- La théorie de Lorentz et les expériences de Zeeman. Éclairage électrique 11, pp. 481–489. Cited by: footnote 18.
- Sur la polarisation par diffraction. Acta mathematica 20, pp. 313–355. External Links: Link Cited by: footnote 13.
- Électricité et optique: la lumière et les théories électrodynamiques. Carré et Naud, Paris. External Links: Link Cited by: footnote 20.
- Sur la dynamique de l’électron. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 140, pp. 1504–1508. External Links: Link Cited by: footnote 34.
- Sur la dynamique de l’électron. Rendiconti del circolo matematico di Palermo 21, pp. 129–176. External Links: Link Cited by: footnote 32, footnote 34.
- La dynamique de l’électron. Revue générale des sciences pures et appliquées 19, pp. 386–402. External Links: Link Cited by: footnote 37.
- La mécanique nouvelle. Revue scientifique 12, pp. 170–177. External Links: Link Cited by: footnote 42.
- Die neue Mechanik. Himmel und Erde 23, pp. 97–116. External Links: Link Cited by: footnote 41.
- L’espace et le temps. Scientia (Rivista di Scienza) 12 (25), pp. 159–170. External Links: Link Cited by: footnote 58.
- The Young Einstein: The Advent of Relativity. Adam Hilger, Bristol. Cited by: footnote 56.
- The relativity revolution in Germany. See The Comparative Reception of Relativity, Glick, pp. 59–111. Cited by: footnote 2.
- The Genesis of General Relativity, Volume 3: Theories of Gravitation in the Twilight of Classical Physics, Between Mechanics, Field Theory, and Astronomy. Springer, Berlin. Cited by: S. A. Walter (2007a).
- Recherches critiques sur l’électrodynamique générale. Annales de chimie et de physique 13, pp. 145–275. Cited by: footnote 23.
- Henri Poincaré, des mathématiques à la philosophie : étude du parcours intellectuel, social et politique d’un mathématicien au début du siècle. Éditions du Septentrion, Lille. External Links: Link Cited by: footnote 29.
- Zu den Wechselbeziehungen zwischen Mathematik und Physik an der Universität Leipzig in der Zeit von 1830 bis 1904/05. Abhandlungen der Sächsischen Akademie der Wissenschaften zu Leipzig, Mathematisch-naturwissenschaftliche Klasse 63 (1), pp. 1–132. Cited by: footnote 10.
- Rockefeller and the Internationalization of Mathematics between Two World Wars: Documents and Studies for the Social History of Mathematics in the 20th Century. Birkhäuser, Basel. Cited by: footnote 7.
- Mathematische Theorie der Diffraction. Mathematische Annalen 47, pp. 317–374. External Links: Link Cited by: footnote 31.
- Zur Relativitätstheorie, I: Vierdimensionale Vektoralgebra. Annalen der Physik 337, pp. 749–776. Cited by: footnote 49.
- Zur Relativitätstheorie, II: Vierdimensionale Vektoranalysis. Annalen der Physik 338, pp. 649–689. Cited by: footnote 49.
- Mathematical Theory of Diffraction. Birkhäuser, Boston. Cited by: footnote 31.
- Poincaré’s Thermodynamics. Nature 45, pp. 245–246. External Links: Link Cited by: footnote 17.
- Hermann Minkowski et la mathématisation de la théorie de la relativité restreinte, 1905–1915. Ph.D. Thesis, Université Paris 7, Paris. External Links: Link Cited by: Figure 1, Figure 2, footnote 1, footnote 53.
- Minkowski, mathematicians, and the mathematical theory of relativity. See The Expanding Worlds of General Relativity, Goenner et al., Einstein Studies, Vol. 7, pp. 45–86. External Links: Link Cited by: footnote 48.
- Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910. See The Genesis of General Relativity, Volume 3: Theories of Gravitation in the Twilight of Classical Physics, Between Mechanics, Field Theory, and Astronomy, Renn and Schemmel, pp. 193–252. External Links: Link Cited by: footnote 32.
- La correspondance d’Henri Poincaré, Volume 2: La correspondance entre Henri Poincaré et les physiciens, chimistes et ingénieurs. Birkhäuser, Basel. External Links: Link Cited by: footnote 17, footnote 19, footnote 21, footnote 25, footnote 33, footnote 57.
- Hermann Minkowski’s approach to physics. Mathematische Semesterberichte 55 (2), pp. 213–235. External Links: Link Cited by: footnote 32.
- Hypothesis and convention in Poincaré’s defense of Galilei spacetime. See The Significance of the Hypothetical in the Natural Sciences, Heidelberger and Schiemann, pp. 193–219. External Links: Link Cited by: footnote 50, footnote 58.
- Masters of Theory: Cambridge and the Rise of Mathematical Physics. University of Chicago, Chicago. Cited by: footnote 2.
- Some Strangeness in the Proportion. Addison-Wesley, Reading, MA. Cited by: A. I. Miller (1980).
- Lignes doubles et triples dans le spectre, produites sous l’influence d’un champ magnétique extérieur. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 124, pp. 1444–1445. External Links: Link Cited by: §2.