Minkowski’s Modern World
Corrected version of Chapter 2 in V. Petkov, ed, Minkowski Spacetime: A Hundred
Years Later, Springer, 2010, pp. 43–61; post-publication corrections appear in red.
Contents
When Hermann Minkowski’s first paper on relativity theory [28] appeared in April 1908, it was met with an immediate, largely critical response. The paper purported to extend the reach of the principle of relativity to the electrodynamics of moving media, but one of the founders of relativity theory, the young Albert Einstein, along with his co-author Jakob Laub, found Minkowski’s theory to be wanting on physical and formal grounds alike. The lesson in physics delivered by his two former students did not merit a rejoinder, but their summary dismissal of his sophisticated four-dimensional formalism for physics appears to have given him pause.
The necessity of such a formalism for physics was stressed by Minkowski in a lecture entitled “Raum und Zeit,” delivered at the annual meeting of the German Association for Natural Scientists and Physicians in Cologne, on 21 September 1908. Minkowski argued famously in Cologne that certain circumstances required scientists to discard the view of physical space as a Euclidean three-space, in favor of a four-dimensional world with a geometry characterized by the invariance of a certain quadratic form. Delivered in grand style, Minkowski’s lecture struck a chord among scientists and philosophers, and upon publication, generated a reaction that was phenomenal in terms of sheer publication numbers and disciplinary breadth.
Historians have naturally sought to explain this burst of interest in relativity theory. According to one current of thought, Minkowski added nothing of substance to Einstein’s theory of relativity, but expressed relativist ideas more forcefully and memorably than Einstein [18, 17]. An alternative explanation claims that Minkowski’s explicit appeal to “pre-established harmony” between pure mathematics and physics resonated with Wilhelmine scientists and philosophers, just when Leibnizian ideas were undergoing a revival in philosophical circles [37].
In this paper I want to suggest that much of the excitement generated by Minkowski’s Cologne lecture among scientists and philosophers arose from an idea that was scandalous when announced on September 21, 1908, but which was soon assimilated, first by theorists and then by the scientific community at large: Euclidean geometry was no longer adequate to the task of describing physical reality, and had to be replaced by the geometry of a four-dimensional space Minkowski called the “world.” Such an affirmation engaged implicitly with the Riemann-Helmholtz-Lie-Poincaré problem of space, and flatly contradicted Poincaré’s conventionalist philosophy, whereby the geometry assigned to physical space is a matter of choice, not necessity.
The first section sketches the background to physical geometry at the time of Minkowski’s first lecture on relativity in 1907, and in the second section, the emergence and evolution of the concept of the “world” in Minkowski’s writings is discussed, along with a reconstruction of the related discovery of “worldlines.” In the third section, the reaction sustained by Minkowski’s radical worldview on the part of a few of his most capable readers in physics is reviewed.
1 The geometry of physical space circa 1907
For the few who had followed advances in the electrodynamics of moving bodies up to 1907, including the papers on this topic by Lorentz, Poincaré and Einstein, in Dutch, English, French, and German, the sources of confusion were many and varied about what was physically significant in these theories and what was not. For example, Lorentz employed a coordinate transformation that was meant to be composed with a Galilean transformation, where Poincaré and Einstein folded the two steps into a single transformation, which Poincaré called the “Lorentz” transformation. Poincaré referred to primed and unprimed Lorentz transformations corresponding to motion and relative rest, but within a single frame of reference [49], obviating recourse to the synchronization of clocks, a topic central to Einstein’s presentation of relativistic kinematics.11endnote: 1 This account draws on standard histories of the special theory of relativity [27, 5].
On other points, there was obvious agreement between the first three relativists. For example, all agreed that bodies in motion undergo a certain contraction in the direction of motion; this was the well-known Lorentz-FitzGerald contraction. For Poincaré and Einstein, the law of velocity composition was such that the speed of light in vacuum was a maximal velocity, in contradiction with classical mechanics, which features no such speed limit.
The law of velocity composition was a sticking point for physicists, according to one observer, who described it as a “strange result” of Einstein’s theory [45]. Einstein derived his law directly from the Lorentz transformation, and expressed it as follows:
| (1) |
where and are the velocities to compose, the angle formed by the velocities, and the velocity of light [6]. Einstein noted that the parallelogram law of classical kinematics was now valid only in first-order approximation. The focus on a limit relation with the Newtonian (Euclidean) case of the addition law was typical of Einstein’s reasoning.
Poincaré, on the other hand, was known to be more of a conquerer than a colonizer in science, and this reputation is borne out by his contribution to relativity theory [57]. For example, Poincaré observed that a Lorentz transformation is a rotation in a four-dimensional vector space with coordinates , , , and [35]. He used this knowledge to form quadruplets equivalent to modern four-vectors of radius, velocity, force and force density, for application in a Lorentz-invariant law of gravitation. Remarkably, the details of his derivation show that he did not approach his quadruplets as so many directed four-vectors, but as simple Lorentz-invariant quantities. In a word, when Poincaré introduced his four-dimensional vector space, he was not thinking primarily in terms of modern four-vectors [55].
Another important feature of relativity theory noted by Poincaré was the significance of Lorentz’s electron theory for classical length measurement. Poincaré asked rhetorically how we go about measuring, and answered as follows [35, p. 132]:
The first response will be: we transport objects considered to be invariable solids, one on top of the other. But that is no longer true in the current theory if we admit the Lorentzian contraction. In this theory, two lengths are equal, by definition, if they are spanned by light in equal times.
Unlike the standard (Helmholtzian) definition of length congruence based on the free mobility of solids, length congruence in Lorentz’s theory depends on the light standard. What Poincaré pointed out, albeit obliquely, was a conflict between the traditional notion of rigidity and the principle of relativity. There are, in fact, no rigid rods in Poincaré’s theory of relativity, in stark contrast with Einstein’s theory.
According to the doctrine of physical space Poincaré developed in the 1890s, the fact that geometry is an abstract science precludes any knowledge of the geometry of physical space, since the identification of geometric objects (points, lines, planes) with physical processes (lightrays, axes of rotation of regular solids) is arbitrary. His view was essentially equivalent to that of Helmholtz, who recognized the possibility of constructing a non-Newtonian physics based on hyperbolic geometry. But in contrast to Helmholtz, Poincaré insisted on the impossibility of an empirical foundation of the geometry of space, and predicted that Euclidean geometry would forever remain the most convenient geometry [58].
Poincaré recognized as early as 1898 that time and simultaneity were not absolutely given by phenomena, and noted several practical methods of clock synchronization, including clock transport and the exchange of telegraphic signals [33]. Most notably, Poincaré had the genial idea in 1900 of defining operationally Lorentz’s “Ortszeit” or local time, as the first-order result of clock synchronization via light signals for two observers relatively at rest, in common motion with respect to the ether, and assuming light isotropy but ignoring the common motion.22endnote: 2 For a derivation, see [4]. Poincaré’s discovery is linked to his activities as a member of the Bureau of Longitudes in [8]; transcriptions of related letters and reports may be consulted at the Henri Poincaré Papers website (henripoincarepapers.univ-nantes.fr). For Poincaré, his operational definition of local time imbued it with physical meaning. Nonetheless, in his view, local time remained distinct from the “true” time kept by clocks at rest with respect to the ether. And although the local time definition mixed quantities of length and time (using modern notation):
where is the frame velocity, is the spatial separation of the two clocks, and is the general (ether) time, Poincaré did not perceive any threat here to his conventionalist doctrine of physical space.
In the first years of the twentieth century, many theorists in electrodynamics were familiar with Poincaré’s doctrine of physical space and operational definition of local time. That Einstein should employ a synchronization procedure identical to Poincaré’s in his first relativity paper is quite natural. In a letter to his friend Habicht, Einstein wrote that his theory involved a “modification of the theory of space and time” [21, Doc. 26]. From kinematic assumptions and light-speed invariance, after much calculation both fastidious and subtle [26], Einstein managed to derive the Lorentz transformation, thereby setting his new physics of inertial frames on sure logical ground.
Einstein’s remark to Habicht suggested that his relativity paper would modify the theory of time and space, and the kinematic section of his paper certainly lives up to this billing. The young Einstein had no fear of challenging received wisdom, noisily dismissing from physics the concept of “light-ether,” or “absolutely stationary space,” the introduction of this concept being “superfluous” [6]. For the rest, Einstein proceeded as if the notion of rigid rods could be applied freely in relativity theory.
As for the notion of time, it did not escape Einstein’s attention that it was a path-dependent quantity in his theory. A clock transported with constant speed around a closed curve, Einstein predicted, would show a lag of seconds with respect to a clock at rest, initially synchronized with the mobile clock. For Einstein, this was just another “peculiar consequence” of his kinematic assumptions, offering him no further insight to the theory of space and time [6].33endnote: 3 Einstein tacitly assumed that the mobile clock rate depends only on the first derivative of its position vector with respect to a clock at rest [43, p. 68].
How did scientists respond to the theories of Poincaré and Einstein? Most ignored their discoveries, which seemed at first to concern only electron dynamics. In addition, it appeared that the so-called “Lorentz-Einstein” theory was inconsistent with the latest experimental results.
Late in the year 1907, a young mathematician at MIT, with J.W. Gibbs the co-author of an influential treatise on vector analysis, E.B. Wilson complained [61] that while over the previous forty months physicists had taken “long strides” along the path of electron theory, the mathematical theory of electricity had advanced “comparatively little” since the landmark work of Lorentz. Like many scientists of the time, Wilson understood the measurements of electron deflection by the Bonn experimental physicist Walter Kaufmann to have ruled out Lorentz’s contractile electron. For Wilson, who was a critic of Poincaré’s conventionalist approach to physics, Kaufmann’s results held a somewhat deeper meaning both for physics, and for our knowledge of the universe in general, because as Poincaré’s work had shown, without the Lorentz electron “the principle of relativity cannot subsist.”44endnote: 4 Wilson’s understanding of the consequence of Kaufmann’s results for the principle of relativity was shared by all relativists, including Einstein, at least until Laue [25] recast the dynamics of the contractile electron in four-dimensional terms. For a review of Laue’s analysis, see [19]. Although Poincaré had expressed disdain for a tangible ether, and a certain attachment to the relativity of space [36], Wilson was keen to be done with the principle of relativity. “It is certainly more satisfactory philosophically and scientifically,” Wilson wrote, “to be left with the hope that some day we may be able to distinguish absolute motion than to feel that we shall in nowise be able to do so.”
Wilson’s attachment to absolute space was shared by Lorentz, and by most physicists circa 1907, very few of whom had heard of Einstein’s theory of relativity, and even fewer of whom had engaged with it. In all of 1906, nine individuals published on relativity, and by the end of 1907, the yearly total came to twenty-three. In September 1907, when Einstein, then employed as a patent examiner in Bern, was asked by Johannes Stark to write a review article on relativity, Einstein averred acquaintance with only five papers (by four authors) on the topic, excluding his own work.55endnote: 5 Two of the five papers mentioned by Einstein appeared before his own writings on relativity. Einstein to Johannes Stark, 25 Sept. 1907 [21, Doc. 58].
A month later, Minkowski wrote to Einstein from Göttingen to request an offprint of his first relativity paper [21, Doc. 62]. According to the letter, Minkowski’s immediate objective was to prepare a seminar on the partial differential equations of mathematical physics at the University of Göttingen, co-directed with his colleague and best friend, the mathematician David Hilbert [3]. But less than a month later, on November 5 1907, Minkowski delivered a report [30] on Poincaré’s theory of gravitation [35] and Planck’s recent paper on relativistic dynamics [32] to the Göttingen mathematical society, in which he described his own four-dimensional program for physics, based in part on Einstein’s theory.
2 World-geometry (1907–1908)
From the very start of his lecture to the Göttingen mathematical society, Minkowski announced his intellectual gambit: to replace Euclidean geometry of space and time with a certain four-dimensional space. “The world in space and time,” Minkowski claimed in his opening remarks, “is, in a certain sense, a four-dimensional non-Euclidean manifold.”66endnote: 6 The published version of Minkowski’s talk [30] differs in several key points from the archival typescript (Handschriftenabteilung, Niedersächsische Staats- und Universitätsbibliothek, Göttingen, Math. Archiv 60:3), and excises the concluding paragraph, as noted by Galison [7]. With hindsight, we might imagine the four-dimensional manifold in question to be that of Minkowski spacetime: a Riemannian four-manifold with Minkowski metric.77endnote: 7 The space Minkowski referred to in this lecture was a certain submanifold of (actually, the manifold of orthogonal space coordinates , , and a time coordinate ), formed by pairs of quadruplets for which the quadratic form was invariant under an unspecified real linear transformation. What Minkowski meant by a non-Euclidean manifold, however, was something else altogether [39]. The tip of a four-dimensional velocity vector , , , , Minkowski explained [30, 373],
is always a point on the surface
(2) or, if you wish, on
(3) and represents at the same time the four-dimensional vector from the origin to this point, and this also corresponds to null velocity, to rest, a genuine vector of this sort. Non-Euclidean geometry, of which I spoke earlier in an imprecise fashion, now unfolds for these velocity vectors.
While Minkowski did not bother to unfold the geometry of his velocity vectors, his Göttingen audience would have recognized in (2) the equation of a pseudo-hypersphere of unit imaginary radius, and in (3) its real counterpart, the two-sheeted unit hyperboloid. The hypersphere (2) and the upper sheet () of the hyperboloid (3) had both been popularized by Helmholtz as models of hyperbolic space [13].
Minkowski observed that the conjugate diameters of the hyperboloid (3) give rise to a geometric image of the Lorentz transformation. Any point on (3) can be considered to be at rest, in that it may be taken to lie on a t-diameter. This change of axes corresponds to an orthogonal transformation of both the time and space coordinates which is a Lorentz transformation (putting ). In modern terms, the three-dimensional hyperboloid (3) embedded in four-dimensional Minkowski space affords an interpretation of the Lorentz transformation. This is one of the geometrical insights that was exploited some time later in the form of a spacetime diagram (Fig. 1).
A point of interest here is that Minkowski presented the “world in space and time” as a three-dimensional hyperbolic hypersurface. This world of Minkowski’s was not just another abstract representation of phenomenal space, but physical space itself, even though he felt he had to qualify the affirmation by inserting “in a certain sense” by hand in his typescript (op. cit., note 6).88endnote: 8 Minkowski was not alone in identifying phenomenal space with hyperbolic space, being joined in this stance a few years later by Einstein’s correspondent in Zagreb, the mathematician Vladimir Varičak [54].
This new understanding of the structure of relativistic velocity space was a significant step in the direction Minkowski wanted to move, but further progress was blocked by a flawed definition of four-velocity.99endnote: 9 Minkowski did not employ such four-vector terminology, which was introduced later by Sommerfeld [46]. Applying the method of generalization from three-component vectors to four-component vectors he had applied to find a four-vector potential, four-current density, and four-force density, Minkowski took over the components of the ordinary velocity vector for the spatial part of four-velocity, and added an imaginary fourth component, . This gave him four components of four-velocity, , , , :
| (4) |
Since the components of Minkowski’s quadruplet do not transform like the coordinates of his vector space , , , , they lack what he knew quite well to be an essential property of a four-vector. His error is an interesting one, as it tells us that he did not yet grasp the notion of four-velocity as the four-vector tangent to the worldline of a particle.1010endnote: 10 For a discussion of likely sources of Minkowski’s error, see [55]. To see how the definition of four-velocity follows from the definition of a worldline, let the differential parameter of a worldline be expressed in Minkowskian coordinates by . The 4-velocity vector is naturally defined to be the first derivative with respect to this parameter, (, 2, 3, 4).
Along with a valid four-velocity vector, Minkowski was also missing a four-force vector. With such a spare stock of four-vectors at his disposal, Minkowski’s project of expressing relativistic mechanics in four-dimensional terms could not move forward. From a retrospective standpoint, it is rather striking that Minkowski would characterize his new form of the laws of physics as “virtually the greatest triumph ever shown by the application of mathematics” [30, p. 373], even before he had obtained a working set of four-vectors. The lecture contains several major insights, however, and these probably instilled Minkowski with enough confidence to air his nascent program before the members of the Göttingen mathematical society. For example, Minkowski unveiled what he called a “Traktor,” a six-component entity equivalent to a modern antisymmetric, second-rank tensor, which Minkowski used to represent the electromagnetic field in a four-dimensional version of Maxwell’s field equations.1111endnote: 11 A four-dimensional form of Maxwell’s potential equations was given in 1906 by a mathematical physicist at the University of Messina, Roberto Marcolongo [55].
Five months passed before the mature form of Minkowski’s spacetime theory came to light. Minkowski delivered his new theory to the printer on 21 February 1908, and it appeared in the Göttinger Nachrichten on 5 April under the title “The Basic Equations for Electromagnetic Processes in Moving Bodies” [55, p. 219, note 84]. Compared to his November lecture, the new paper contains a number of cognitive breakthroughs, including a valid four-velocity vector, the notion of proper time as the parameter of a hyperline in spacetime, the light-hypercone structure of spacetime, and the four-dimensional equations of motion of a material particle.
It is not clear how Minkowski accomplished these breakthroughs. Did he reread Poincaré’s memoir, and realize the correct definitions of four-velocity and four-force were readily available? Did he notice that Poincaré’s assumption of a lightlike propagation speed of gravitational action between two points in four-dimensional space could be generalized to obtain a lightcone with origin at the source point? Then again, perhaps reading about path-dependent time in the offprint he’d asked for from Einstein put him on the right track. Or maybe Minkowski worked it all out on his own, by studying the embedding of relativistic velocity space (3) in four-dimensional vector space, and thereby obtaining further insight into the structure of this hyperspace. I’ll return shortly to the latter conjecture.
The result of Minkowski’s labors was a sixty-page technical memoir packed with new notation, terminology, and calculation rules, featuring a total of six references, and no figures. The four-vectors Minkowski had defined in his earlier lecture now appeared in a new form, along with a single new differential operator named lor. As an immediate consequence of this formal extremism, reading Minkowski’s paper was a challenging mathematical endeavor.
Terminology changes in “Basic Equations” concerned the “world” itself: all reference to the “world” vanished from “Basic Equations,” and along with it, all explicit reference to the velocity space on which the term had been predicated. Minkowski began, as in the November lecture, with a manifold, , and identified a submanifold corresponding to physically-significant points, which he now called “spacetime points” (Raum-Zeitpunkte), and “events” (Ereignisse). Minkowski now characterized velocity in terms of the tangent of an imaginary angle i,
| (5) |
where . He could just as well have employed a real angle with a hyperbolic tangent, , but did not, perhaps out of a desire to avoid the taint of non-Euclidean geometry, which was likely to offend physicists. From his earlier geometric interpretation of (3), Minkowski kept the idea that every rotation of a -diameter corresponds to a Lorentz transformation, which he now expressed in terms of the angle :
| (6) |
In all likelihood, Minkowski was aware of the connection pointed out by Einstein between composition of Lorentz transformations and velocity composition, even though he never mentioned it in print. In fact, Minkowski neither mentioned Einstein’s law of velocity addition, nor expressed it mathematically.
While Minkowski suppressed his earlier appeal to the hyperbolic geometry of velocity vectors, he kept the hypersurface (3) on which it was based, and provided a new interpretation of its physical significance. This interpretation represents an important clue to understanding how Minkowski discovered the worldline structure of spacetime.
In the appendix to “Basic Equations” devoted to mechanics, Minkowski rehearsed his geometrical interpretation of (3), according to which any point on this surface could be chosen such that the line formed with the origin forms a new time axis, and corresponds to a Lorentz transformation. He defined a “spacetime line” to be the totality of spacetime points corresponding to any particular point of matter for all time . Obvious as this definition may appear to us, it is missing altogether from his November 5 lecture.
With respect to the new concept of a spacetime line, Minkowski noted that its direction is determined at every spacetime point. Here Minkowski introduced the notion of “proper time” (Eigenzeit), , expressing the increase of coordinate time for a point of matter with respect to :
| (7) |
where is the square of ordinary velocity, , and , which corrects the flawed definition of this fourth component of four-velocity given by Minkowski in his November 5 lecture (4).
It is tempting to suppose that Minkowski was led to the discovery of worldlines and proper time by considering the embedding of the hypersurface (3) in four-dimensional spacetime, given that he later expressed the norm of a four-velocity vector in the similar form:
| (8) |
and noted that the components of four-velocity can be defined in terms of proper time:
| (9) |
From these expressions, it appears that the spacetime line has a tangent at every associated spacetime point, and this tangent corresponds to four-velocity. However, this is not how Minkowski presented his discovery in the “Basic Equations.” A discursive indication supporting this reconstruction is at hand in Minkowski’s description of the “direction” of a given spacetime line, determined at every spacetime point. Also, while Minkowski does not actually tie four-velocity to either (3) or (8) in “Basic Equations,” he does so in the Cologne lecture [29, p. 84], employing yet another form of (3):
| (10) |
where , , , , denote components of four-velocity. The definition of proper time is essential to (8), (9), and (10), but Minkowski remained coy on its origins, describing it only as a “generalization of the concept of local time formed by Lorentz for uniform motion” [28, p. 100]. More than likely, proper time represented much more than this to him. And almost certainly, he viewed (3) as the key to spacetime geometry. In a letter to his good friend, former teacher and colleague Adolf Hurwitz, professor of mathematics in Zurich, Minkowski described the “quintessence of my latest studies” to be the “principle of the hyperbolic world” (Minkowski to Hurwitz, 5 May 1908, Niedersächsische Staats- und Universitätsbibliothek, Math. Archiv 78: 212).
Although Minkowski neglected to connect four-velocity to Einstein’s law of velocity addition, others did this for him, beginning with Sommerfeld, who expressed parallel velocity addition as the sum of tangents of an imaginary angle [45], followed by Varičak, who recapitulated Sommerfeld’s analysis in terms of hyperbolic functions of a real angle [52]. A mathematician at the University of Zagreb, Varičak launched what’s been called the “non-Euclidean style” of Minkowskian relativity [54], characterized by an approach to relativity from the standpoint of hyperbolic geometry, based on Einstein’s velocity addition (1), and Minkowski’s equations (5) and (6). Considered by Sommerfeld as a rival to his own “Euclidean” spacetime formalism, the non-Euclidean style has seen several revivals in various forms over the past century.1212endnote: 12 For a recent effort, see [40].
What Minkowski found praiseworthy in Einstein’s paper was not the law of velocity addition, but the notion of the relativity of simultaneity. Einstein, Minkowski wrote, understood the supposition of Lorentz covariance as being “much more a novel view, imposed by phenomena, of the concept of time [than an] artificial hypothesis” [28, p. 55]. But had his former student really understood the relativity of simultaneity? Minkowski noted in a section of his paper entitled “The concept of time” that the simultaneity of any two events is indeed relative to the motion of the observer (as Einstein had pointed out), just as it is for three simultaneous events, while the simultaneity of four events is absolute, provided the four corresponding spacetime points do not lie on the same spatial plane [28, p. 69]. He showed, in other words, that Einstein’s vertiginous relativity of simultaneity was both grounded and bounded in his four-dimensional view.
Despite its dense and idiosyncratic symbolic notation, Minkowski’s “Basic Equations” incited a quick critical response from two of his former students, Einstein and Laub, who had discovered what they thought was an infelicity in Minkowski’s definition of ponderomotive force density.1313endnote: 13 See [48, Doc. 52], and the editorial note “Einstein and Laub on the electrodynamics of moving media” [48, pp. 503–507]. They also found that following Minkowski’s formalism required too much effort, and set themselves to translating Minkowski’s electrodynamics of moving media in terms of ordinary vector analysis [48, Doc. 51]. One imagines that this came as a disappointment to Minkowski. Another of his former students, Gunnar Nordström followed the same path as Einstein and Laub, by showing in his thesis how to derive Minkowski’s field equations using ordinary vector analysis [31].
Einstein and Laub’s two papers on Minkowski’s theory appeared in the July 7 issue of the Annalen der Physik, and constitute the only comment on the “Basic Equations” to be published before the September meeting of the German Association of Natural Scientists and Physicians in Cologne. The lecture Minkowski prepared for the mathematical section of this meeting, judging from its overdone rhetoric, may be considered as a reaction to the brutal treatment his spacetime theory had received in the Annalen, as Minkowski glorified the discoveries of pure mathematics. Judging from his appeal to Einstein and Lorentz as immediate forebears in the theory of relativity, however, Minkowski aimed also to convince physicists that his spacetime geometry was not entirely useless [53].
In pursuit of the latter goal, Minkowski retrieved the “world” he’d suppressed from the “Basic Equations,” and modified its definition. The world as Minkowski now defined it was no longer the hyperbolic space of velocity vectors, but simply the “manifold of all thinkable systems of values , , , ,” or what we might call . The geometric objects introduced in “Basic Equations” were renamed accordingly, such that spacetime points segued into worldpoints, spacetime lines into worldlines, and so on. Henceforth, Minkowski’s world was no different from the manifold of classical physics, only the geometry had changed.
The redefinition of the “world” is a telling one, as it moved Minkowski’s spacetime theory toward the mainstream of scientific thought, and signalled his interest in capturing an audience of physicists. Further evidence of this strategy is provided by the fact that Minkowski retained the two-sheeted hyperboloid (3) of his two earlier writings on relativity, but dropped all mention of non-Euclidean geometry. Suppressing the and coordinates, Minkowski illustrated (3) graphically. Incorporating the asymptotes of (3), interpreted as the set of worldpoints capable of sending light to the origin, or receiving light from the origin, i.e., forward and aft null hypercones, and a second pair of symmetric axes and , Minkowski provided a simple and appealing graphic model of spacetime (see Fig. 1).
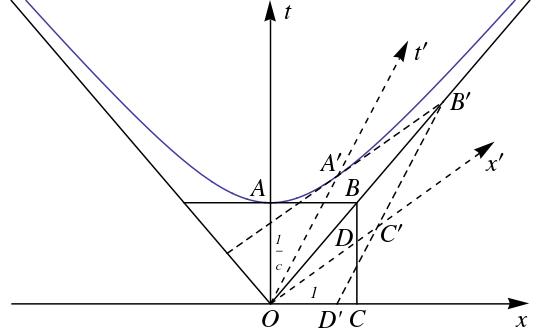
The transformations leaving (3) invariant, combined with arbitrary displacements of the origin, give rise to the inhomogeneous Lorentz group, or what Minkowski referred to simply as . Minkowski naturally affirmed the laws of physics to be invariant with respect to , and interpreted this invariance with reference to his spacetime diagram (Fig. 1). According to Minkowski’s interpretation, once time is designated ,
space must then in this connection necessarily be defined by the three-parameter manifold , , , so that physical laws would be expressed in exactly the same way by means of , , , as by means of , , , .
The significance of this remark was twofold. In the first place, for Minkowski the “world” of physical phenomena was no longer characterized by one space (as in Newtonian mechanics), but by “unendlessly many” spaces. In other words, Minkowski underlined the fact that any particle in motion may be considered to be at rest, and can be used to define a time axis and a constant-time hyperplane passing through the origin normal to this axis. Since the choice of particle is arbitrary, the latter hyperplane is only one of an infinity of Euclidean spaces that we may consider in spacetime geometry.1414endnote: 14 Minkowski argued further that Einstein had not recognized this relativity of space, an argument deemed uncharitable, at best, in [53].
Secondly, the idea that a given definition of time necessarily entails a certain definition of space clearly contradicted Poincaré’s doctrine of physical space. To drive his point home, Minkowski famously observed:
Three-dimensional geometry becomes a chapter of four-dimensional physics. You see why I stated at the outset that space and time should sink into the shadows and only a world in itself subsist.
Where Poincaré had considered three-dimensional geometry to form an inseparable pair with classical physics [58], and had memorably compared physical science to a library, with the theorist in charge of inventory and cataloguing and the experimentalist in charge of acquisitions [34], Minkowski managed to subvert both images in one fell swoop.
Although Minkowski did not mention Poincaré’s name in the course of the Cologne lecture, an omission several mathematicians found odd [53], the French mathematician’s doctrine of physical space was an obvious target for him. Poincaré had argued that time and space are not given to us through phenomena, but are the result of conventions. Cognitively endowed by nature with the general notion of a group, humans had adopted Euclidean geometry because the displacement of solid bodies closely approximates the motions of the Euclid group, Poincaré argued [58].1515endnote: 15 Along with Poincaré, but for different reasons, Felix Hausdorff claimed that there was no means of settling the question of the geometry of physical space [11]. Consequently, Minkowski’s affirmation of the necessity of spacetime for understanding physics implicitly contradicted Hausdorff’s view along with that of Poincaré.
Minkowski’s anti-conventionalism extended beyond space to include time, or rather, spacetime. This is what he meant, of course, when he said that both space and time should sink into the shadows: any moving particle could be considered to be instantaneously at rest, and any particle at rest could be considered to be in motion with any sublight velocity. The new views of space and time were not mere scenarios, Minkowski insisted, but were imposed on scientists by the circumstances. This was a bold position to adopt in September 1908, as the theory of relativity was then held to be inconsistent with Kaufmann’s cathode-ray deflection measurements, as mentioned in (§ 1). Minkowski deftly ignored the latter experiments, and took for granted the compatibility of relativity theory with observation.
What were the circumstances that forced a change in conceptions of space and time? This came down to two items in Minkowski’s presentation, one formal, the other empirical. The formal consideration was Lorentz-covariance of the differential wave equation of light propagation in empty space. On the empirical side, Minkowski cited the null result of the Michelson-Morley ether-drift experiment. Both of these items had been acknowledged earlier by Lorentz and Poincaré, neither one of whom thought at the time that the traditional concepts of space and time required an overhaul, or even minor repair. Instead, to address the Michelson-Morley null result the latter two theorists appealed to the contraction of moving bodies in the direction of motion with respect to the absolute ether, known as the Lorentz-FitzGerald contraction. The Lorentz-covariance of the wave equation of light was assured by the principle of relativity, upheld by both Lorentz and Poincaré.
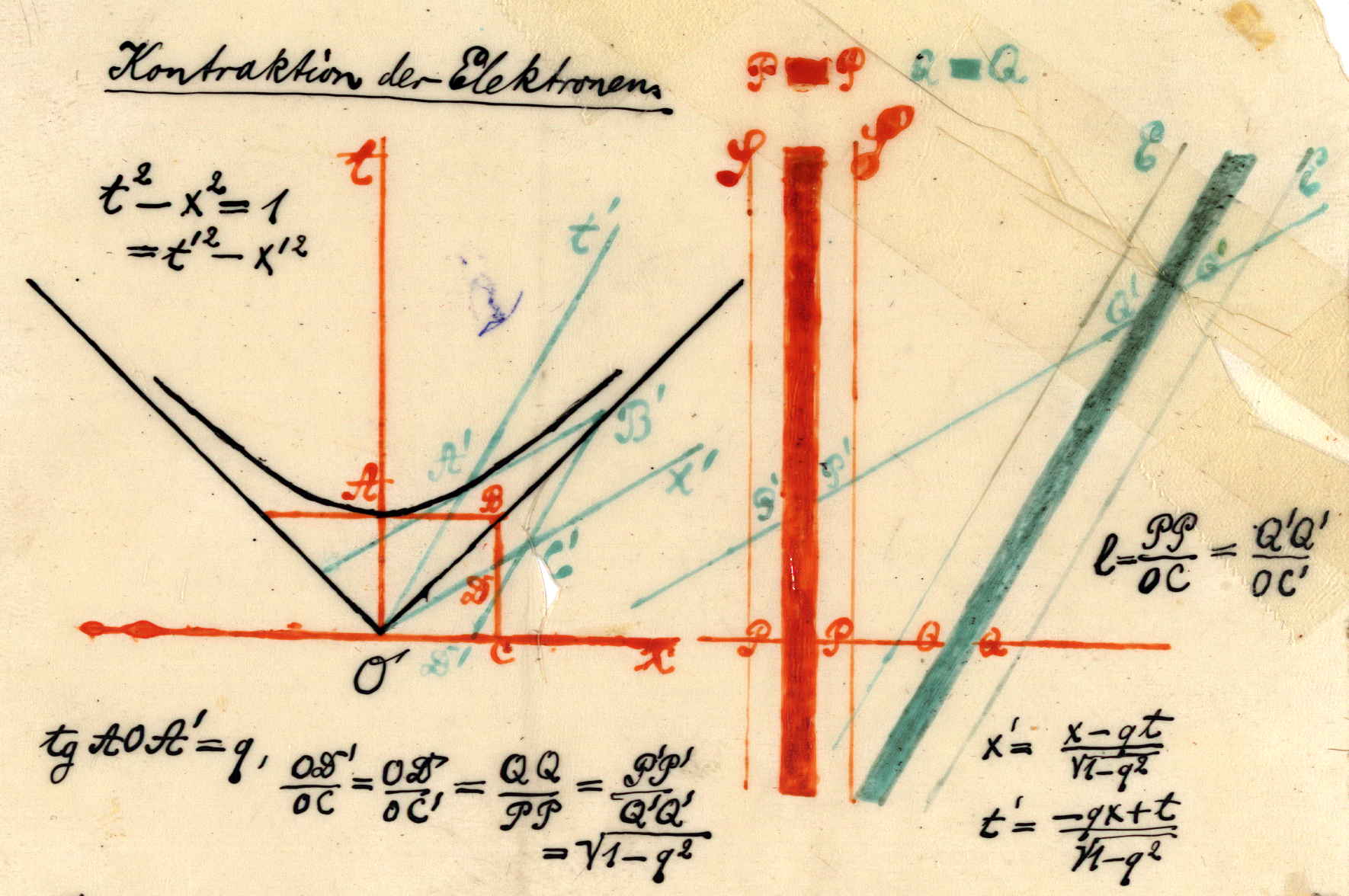
Since Minkowski also upheld the principle of relativity, he naturally focused his attention on what distinguished his view from that of Lorentz and Poincaré: the Lorentz-FitzGerald contraction. He suggested that the contraction need not be considered, as he felt it was in Lorentz’s view, a “gift from above” (als Geschenk von oben). Rather, he wrote, “the Lorentzian hypothesis is fully equivalent to the new view of space and time, whereby it becomes much more comprehensible.” Referring to a spacetime diagram (see Fig. 2), Minkowski considered the length of two equivalent electrons, one at rest, the other in uniform motion. The details of his demonstration need not be reproduced here,1616endnote: 16 For demonstrations of the relativity of simultaneity, time dilation, and length contraction using a spacetime diagram, see [51, p. 98]. but if we recall Poincaré’s proof of electron contraction from Lorentz covariance [35], it is interesting to note Minkowski’s choice of “Lorentz electrons” as the bodies of reference, instead of, say, generic solids. Turning the table on Poincaré, Minkowski deduced Lorentz-FitzGerald contraction of electrons from the geometrical relations of spacetime. The structure of spacetime, in other words, was given epistemic priority over the structure of electrons, and consequently over all of physics, in the prevalent microphysical reduction.
3 The reception of “Raum und Zeit”
The text of the lecture “Raum und Zeit” went through at least four drafts, one of which dates from 24 April 1908, before Minkowski submitted it for publication in mid-December 1908. Before the end of 1909, it had appeared in full French and Italian translation and partial English translation, followed by a Russian translation in 1910. Minkowski did not live to see these publications, as he expired on 12 January 1909, following an operation for appendicitis.1717endnote: 17 Minkowski also missed a lecture series by Poincaré, organized by Hilbert for the last week of April in Göttingen. On Poincaré’s visit, see the notes in Vol. 2 of the Poincaré Correspondence [56, p. 377], the Hilbert-Poincaré letters (henripoincarepapers.univ-nantes.fr), and David Rowe’s transcription of two lectures Hilbert delivered for the occasion [41].
The published version of “Raum und Zeit” sparked an explosion of publications in relativity theory, with the number of papers on relativity tripling between 1908 (32 papers) and 1910 (95 papers) [53]. As Hentschel’s study showed, the theory of relativity was many things to many people [15], and the same conclusion clearly applies to Minkowski’s spacetime theory. For example, a disciplinary analysis of the reception of Minkowski’s lecture reveals a overwhelmingly positive response on the part of mathematicians, and a decidedly mixed reaction on the part of physicists [53]. In this section, I suggest that what physicists objected to most in Minkowski’s Cologne lecture was the idea that Euclidean space was no longer adequate for understanding physical phenomena.
Part of the ultimate success of Minkowski’s ideas may be attributed to the fact that they were taken up by several members of the Göttingen scientific community, including the titular professors David Hilbert, Felix Klein, Emil Weichert, and former professors Gustav Herglotz and Karl Schwarzschild. In addition, several of Minkowski’s former students in Göttingen took up the theory, including Max Born, Max Laue, Theodor Kaluza, Gunnar Nördstrom, Philipp Frank, Emmy Noether, and Ernst Hellinger. As Rowe has remarked [42], the eventual success of Minkowski’s theory was a “major triumph” for the Göttingen mathematical community.
Minkowski’s Göttingen colleagues had a hand in disseminating Minkowski’s work after his death, and in extending its reach in mechanics and electrodynamics, in particular. The individual contributing the most to the success of spacetime geometry among physicists, however, was neither a Göttingen colleague nor a former student, but a friend from Minkowski’s schooldays in Königsberg: the Munich theorist Arnold Sommerfeld [1, p. 72]. A former assistant to Klein in Göttingen, and an outsider in theoretical physics, Sommerfeld was initially skeptical of Einstein’s relativity, but let himself be won over by Minkowski’s theory. Sommerfeld promoted spacetime theory as a technical simplification, which rendered “irrelevant” the “troublesome calculations” of Lorentz and Einstein [53]. Sommerfeld went on to devise a four-dimensional vector algebra and analysis, using symbolic notation and differential operators consonant with those he had imposed on authors as editor of the physics volumes of Klein’s vast project, the Encyclopedia of Mathematical Sciences including Applications [44]. His streamlined spacetime formalism was taken over and extended by Max Laue, then working in Sommerfeld’s institute in Munich, for use in the first German textbook on relativity theory [24]. Laue’s textbook was hugely successful, and effectively established the Sommerfeld-Laue formalism as the standard for research in relativity physics.
Sommerfeld insisted upon the simplification afforded to calculation by the adoption of a spacetime approach, and left aside Minkowski’s philosophical interpretation of spacetime, with one exception. In the introduction to his 1910 reformulation of Minkowski’s matrix calculus, Sommerfeld echoed Minkowski’s belief that absolute space should vanish from physics, to be replaced by the “absolute world,” by which he meant spacetime geometry, and not [46, p. 749]. This exchange of absolutes, Euclidean space for Minkowski spacetime, was designed to calm physicists shocked by Minkowski’s high-handed dismissal of Euclidean space as the frame for understanding physical phenomena.
Among the shocked physicists was Dantzig’s Max Wien, cousin of Willy Wien, the co-editor of Annalen der Physik. In a letter to Sommerfeld, Max Wien described his reaction to reading Minkowski’s Cologne lecture, which gave him, he wrote, “a slight brain-shiver, now space and time appear conglomerated together in a gray, miserable chaos” [1, p. 71]. Willy Wien was shocked, too, but it wasn’t the loss of Euclidean space that bothered him so much as Minkowski’s claim that circumstances forced spacetime geometry on physicists. The entire Minkowskian system, Wien said in a 1909 lecture, “evokes the conviction that the facts would have to join it as a fully internal consequence.” Wien would have none of this, as he felt that the touchstone of physics was experiment, not abstract mathematical deduction. “For the physicist,” Wien concluded his lecture, “Nature alone must make the final decision” [54].
Another physicist, Minkowski’s former colleague and director of the Göttingen Institute for Geophysics, Emil Wiechert welcomed Minkowski’s spacetime theory, but felt there was no need to dismiss absolute space. Following a remark made by Minkowski in “Raum und Zeit,” Wiechert proposed to recover the notion of direction in Euclidean space with what he called “Schreitung” in spacetime, or what amounted to the direction of a four-velocity vector [59]. As for Minkowski’s claim that a new intuition of space and time was required, this did not bother Wiechert at all. In a non-technical review of relativity theory [60], Wiechert wrote that the special relativity theory was “brought by Minkowski to a highly mathematically-finished form.” He continued:
It was also Minkowski who, with bold courage, drew the extreme consequences of the theory for a new spacetime-intuition [Raumzeitanschauung] and contributed so very much to the theory’s renown.
It was precisely Minkowski’s spacetime-intuition, or his identification of the extreme consequences of this intuition, that had made the theory of relativity famous in Wiechert’s view. For Wiechert, however, all intuitions, including ether, and matter in motion, were but anthropomorphic “images,” the reality of which was beyond our ken [59].
A view similar to Wiechert’s was expressed by Max Laue in his influential relativity textbook. Laue considered Minkowski spacetime as an “almost indispensable resource” for precise mathematical operations in relativity [24, p. 46]. He expressed reservations, however, about Minkowski’s philosophy, in that the geometric interpretation (or “analogy”) of the Lorentz transformation called upon a space of four dimensions:
[A] geometric analogy can exist only in a four-dimensional manifold. That this is inaccessible to our intuition should not frighten us; it deals only with the symbolic presentation of certain analytical relationships between four variables.
One could avail oneself of the new four-dimensional formalism, Laue assured his readers, even if one was not blessed with Minkowski’s spacetime-intuition, and without committing oneself to the existence of Minkowski’s four-dimensional world.
By disengaging Minkowski’s spacetime ontology from the Sommerfeld-Laue spacetime calculus, Laue cleared the way for the acceptance by physicists of both his calculus, and spacetime geometry in general. A detailed study of the reception of Minkowski’s ideas on relativity has yet to be realized, but anecdotal evidence points to a change in attitudes toward Minkowski’s spacetime view in the 1950s. For example, in the sixth edition of Laue’s textbook, celebrating the fiftieth anniversary of relativity theory, and marking the end of Einstein’s life, its author still felt the need to warn physicists away from Minkowski’s scandalous claim in Cologne that space and time form a unity. As if in defiance of Laue, this particular view of Minkowski’s (“Von Stund’ an …”) was soon cited (in the original German) on the title page of a rival textbook on special relativity [50]. In Laue’s opinion, however, Minkowski’s most famous phrase remained an “exaggeration” [23, p. 60].
Four generations of physicists, dating from the first edition of Laue’s textbook, have learned relativity theory in terms of four-vectors and Minkowski maps. Regular application of the Sommerfeld-Laue formalism and spacetime diagrams over the last century has familiarized scientists with spacetime geometry quite thoroughly, making way for numerous variants and extensions. The rules of spacetime diagrams found their way into Feynman diagrams in the 1950s, extending their reach into particle physics, although once again, some physicists objected to their use on the grounds that it was inappropriate to portray trajectories of real particles in this way [20].
4 Minkowski’s modern world
Minkowski’s carefully-crafted Cologne lecture shocked scientists’ sensibilities, in sharp contrast to all previous writings on relativity, including his own. In modernist style, he piled provocation upon provocation: the disciplinary rhetoric, the spate of neologisms, the self-serving (and quite fictional) account of the discovery of spacetime, the anti-conventionalist charge, the discounting of Poincaré, the disingenuous account of Einstein’s kinematics, and the geometrical explanation of electron contraction and gravitational attraction, all combine to make “Raum und Zeit” a magnificent example of scientific agitprop.
There was more to the Cologne lecture than mere provocation, of course, as Minkowski took care to place his theory in a distinguished lineage leading from Lorentz, Liénard, Wiechert, Schwarzschild, Einstein and Planck. He claimed not only to have surpassed Lorentz and Einstein, but to have provided a theory of gravitation on an observational par with that of Newton, and to have crafted an electron-based theory of electrodynamics of moving media superior to that of Lorentz. All these claims turned out to be true, adding credibility to the whole, and prompting Arnold Sommerfeld to remark, five years later, that “there is nothing in what Minkowski says that must now be withdrawn.” Sommerfeld admitted only one exception: the theory of gravitation, where Einstein’s field theory appeared preferable to the action-at-a-distance approaches of Poincaré and Minkowski [47].
The author of “Raum and Zeit” famously characterized his intuitions (Anschauungen) of space and time as grounded in experimental physics, and radical in nature. Predictably, his lecture created a scandal for physicists in its day, but unlike most scandals, it did not fade away with the next provocation. Instead, Minkowski focused attention on how mathematics structures our understanding of the physical universe, in a way no other writer had done since Riemann, or has managed to do since, paving the way for acceptance of even more visually-unintuitive theories to come in the early twentieth century, including general relativity and quantum mechanics. Minkowski’s provocation of physicists in Cologne, his rejection of existing referents of time, space, and geometry, and his appeal to subjective intuition to describe external reality may certainly be detached from Minkowski geometry, as Laue and others wished, but not if we want to grasp how the concept of spacetime reshaped physics in the early twentieth century.
Notes
- 1 This account draws on standard histories of the special theory of relativity [27, 5].
- 2 For a derivation, see [4]. Poincaré’s discovery is linked to his activities as a member of the Bureau of Longitudes in [8]; transcriptions of related letters and reports may be consulted at the Henri Poincaré Papers website (henripoincarepapers.univ-nantes.fr).
- 3 Einstein tacitly assumed that the mobile clock rate depends only on the first derivative of its position vector with respect to a clock at rest [43, p. 68].
- 4 Wilson’s understanding of the consequence of Kaufmann’s results for the principle of relativity was shared by all relativists, including Einstein, at least until Laue [25] recast the dynamics of the contractile electron in four-dimensional terms. For a review of Laue’s analysis, see [19].
- 5 Two of the five papers mentioned by Einstein appeared before his own writings on relativity. Einstein to Johannes Stark, 25 Sept. 1907 [21, Doc. 58].
- 6 The published version of Minkowski’s talk [30] differs in several key points from the archival typescript (Handschriftenabteilung, Niedersächsische Staats- und Universitätsbibliothek, Göttingen, Math. Archiv 60:3), and excises the concluding paragraph, as noted by Galison [7].
- 7 The space Minkowski referred to in this lecture was a certain submanifold of (actually, the manifold of orthogonal space coordinates , , and a time coordinate ), formed by pairs of quadruplets for which the quadratic form was invariant under an unspecified real linear transformation.
- 8 Minkowski was not alone in identifying phenomenal space with hyperbolic space, being joined in this stance a few years later by Einstein’s correspondent in Zagreb, the mathematician Vladimir Varičak [54].
- 9 Minkowski did not employ such four-vector terminology, which was introduced later by Sommerfeld [46].
- 10 For a discussion of likely sources of Minkowski’s error, see [55]. To see how the definition of four-velocity follows from the definition of a worldline, let the differential parameter of a worldline be expressed in Minkowskian coordinates by . The 4-velocity vector is naturally defined to be the first derivative with respect to this parameter, (, 2, 3, 4).
- 11 A four-dimensional form of Maxwell’s potential equations was given in 1906 by a mathematical physicist at the University of Messina, Roberto Marcolongo [55].
- 12 For a recent effort, see [40].
- 13 See [48, Doc. 52], and the editorial note “Einstein and Laub on the electrodynamics of moving media” [48, pp. 503–507].
- 14 Minkowski argued further that Einstein had not recognized this relativity of space, an argument deemed uncharitable, at best, in [53].
- 15 Along with Poincaré, but for different reasons, Felix Hausdorff claimed that there was no means of settling the question of the geometry of physical space [11]. Consequently, Minkowski’s affirmation of the necessity of spacetime for understanding physics implicitly contradicted Hausdorff’s view along with that of Poincaré.
- 16 For demonstrations of the relativity of simultaneity, time dilation, and length contraction using a spacetime diagram, see [51, p. 98].
- 17 Minkowski also missed a lecture series by Poincaré, organized by Hilbert for the last week of April in Göttingen. On Poincaré’s visit, see the notes in Vol. 2 of the Poincaré Correspondence [56, p. 377], the Hilbert-Poincaré letters (henripoincarepapers.univ-nantes.fr), and David Rowe’s transcription of two lectures Hilbert delivered for the occasion [41].
References
- [1] (1975) Arnold Sommerfeld: Lehrer und Forscher an der Schwelle zum Atomzeitalter, 1868-1951. Wissenschaftliche Verlagsgesellschaft, Stuttgart. Cited by: §3, §3.
- [2] O. Blumenthal (Ed.) (1913) Das Relativitätsprinzip; Eine Sammlung von Abhandlungen. Teubner, Leipzig. link1 Cited by: 47.
- [3] (2004) David Hilbert and the Axiomatization of Physics (1898–1918): From Grundlagen der Geometrie to Grundlagen der Physik. Kluwer, Dordrecht. Cited by: §1.
- [4] (1995) Henri Poincaré’s criticism of fin de siècle electrodynamics. Studies in History and Philosophy of Modern Physics 26, pp. 1–44. Cited by: endnote 2.
- [5] (2000) Electrodynamics from Ampère to Einstein. Oxford University Press, Oxford. link1 Cited by: endnote 1.
- [6] (1905) Zur Elektrodynamik bewegter Körper. Annalen der Physik 322, pp. 891–921. link1 Cited by: §1, §1, §1.
- [7] (1979) Minkowski’s spacetime: from visual thinking to the absolute world. Historical Studies in the Physical Sciences 10, pp. 85–121. Cited by: endnote 6.
- [8] (2003) Einstein’s Clocks and Poincaré’s Maps: Empires of Time. Norton, New York. Cited by: endnote 2.
- [9] H. Goenner, J. Renn, T. Sauer, and J. Ritter (Eds.) (1999) The Expanding Worlds of General Relativity. Birkhäuser, Boston/Basel. Cited by: 53.
- [10] J. Gray (Ed.) (1999) The Symbolic Universe: Geometry and Physics, 1890–1930. Oxford University Press, Oxford. Cited by: 54.
- [11] (1904) Das Raumproblem. Annalen der Naturphilosophie 3, pp. 1–23. Cited by: endnote 15.
- [12] M. Heidelberger and G. Schiemann (Eds.) (2009) The Significance of the Hypothetical in the Natural Sciences. Walter de Gruyter, Berlin. link2 Cited by: 58.
- [13] (1884) Vorträge und Reden, Volume 2. Vieweg, Braunschweig. link1 Cited by: §2.
- [14] V. F. Hendricks, K. F. Jørgenson, J. Lützen, and S. A. Pedersen (Eds.) (2006) Interactions: Mathematics, Physics and Philosophy, 1860–1930. Springer, Dordrecht. Cited by: 19.
- [15] (1990) Interpretationen und Fehlinterpretationen der speziellen und der allgemeinen Relativitätstheorie durch Zeitgenossen Albert Einsteins. Birkhäuser, Basel. link1 Cited by: §3.
- [16] P. Hinneberg, E. Lecher, and E. Warburg (Eds.) (1915) Die Kultur der Gegenwart, Ihre Entwicklung und Ihre Ziele, 3, Mathematik - Naturwissenschaften - Medizin, 3, Anorganische Naturwissenschaften, 1: Physik. Teubner, Leipzig. link1 Cited by: 60.
- [17] (1968) Theory of relativity and the ether. Japanese Studies in the History of Science 7, pp. 37–53. Cited by: Minkowski’s Modern World Corrected version of Chapter 2 in V. Petkov, ed, Minkowski Spacetime: A Hundred Years Later, Springer, 2010, pp. 43–61; post-publication corrections appear in red..
- [18] (1965) The metaphor of space-time events in science. Eranos Jahrbuch 34, pp. 33–78. Cited by: Minkowski’s Modern World Corrected version of Chapter 2 in V. Petkov, ed, Minkowski Spacetime: A Hundred Years Later, Springer, 2010, pp. 43–61; post-publication corrections appear in red..
- [19] (2006) From classical to relativistic mechanics: electromagnetic models of the electron. See Interactions: Mathematics, Physics and Philosophy, 1860–1930, Hendricks et al., pp. 65–134. Cited by: endnote 4.
- [20] (2000) Stick-figure realism: conventions, reification, and the persistence of Feynman diagrams, 1948–1964. Representations 70, pp. 49–86. Cited by: §3.
- [21] M. J. Klein, A. J. Kox, and R. Schulmann (Eds.) (1993) The Collected Papers of Albert Einstein, Volume 5, The Swiss Years: Correspondence, 1902–1914. Princeton University Press, Princeton. link1 Cited by: §1, §1, endnote 5.
- [22] N. Koertge (Ed.) (2007) New Dictionary of Scientific Biography. Gale, Detroit. Cited by: 57.
- [23] (1955) Die Relativitätstheorie: die spezielle Relativitätstheorie. Vieweg, Braunschweig. Cited by: §3.
- [24] (1911) Das Relativitätsprinzip. Vieweg, Braunschweig. link1 Cited by: §3, §3.
- [25] (1911) Zur Dynamik der Relativitätstheorie. Annalen der Physik 340, pp. 524–542. Cited by: endnote 4.
- [26] (2009) Kinematics: The Lost Origins of Einstein’s Relativity. Johns Hopkins University Press, Baltimore. Cited by: §1.
- [27] (1981) Albert Einstein’s Special Theory of Relativity: Emergence (1905) and Early Interpretation. Addison-Wesley, Reading, MA. Cited by: endnote 1.
- [28] (1908) Die Grundgleichungen für die electromagnetischen Vorgänge in bewegten Körpern. Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, pp. 53–111. link1 Cited by: §2, §2, Minkowski’s Modern World Corrected version of Chapter 2 in V. Petkov, ed, Minkowski Spacetime: A Hundred Years Later, Springer, 2010, pp. 43–61; post-publication corrections appear in red..
- [29] (1909) Raum und Zeit. Jahresbericht der deutschen Mathematiker-Vereinigung 18, pp. 75–88. link1 Cited by: Figure 1, §2.
- [30] (1915) Das Relativitätsprinzip. Jahresbericht der deutschen Mathematiker-Vereinigung 24, pp. 372–382. Cited by: §1, §2, §2, endnote 6.
- [31] (1908) Die Energiegleichung für das elektromagnetische Feld bewegter Körper. Ph.D. Thesis, University of Helsinki, Helsinki. Cited by: §2.
- [32] (1907) Zur Dynamik bewegter Systeme. Sitzungsberichte der königliche preußischen Akademie der Wissenschaften, pp. 542–570. Cited by: §1.
- [33] (1898) La mesure du temps. Revue de métaphysique et de morale 6, pp. 1–13. link1 Cited by: §1.
- [34] (1900) Les relations entre la physique expérimentale et la physique mathématique. Revue générale des sciences pures et appliquées 11, pp. 1163–1175. link1 Cited by: §2.
- [35] (1906) Sur la dynamique de l’électron. Rendiconti del Circolo matematico di Palermo 21, pp. 129–176. link1, link2 Cited by: §1, §1, §1, §2.
- [36] (1907) La relativité de l’espace. Année psychologique 13, pp. 1–17. link1 Cited by: §1.
- [37] (1985) The Young Einstein: The Advent of Relativity. Adam Hilger, Bristol. Cited by: Minkowski’s Modern World Corrected version of Chapter 2 in V. Petkov, ed, Minkowski Spacetime: A Hundred Years Later, Springer, 2010, pp. 43–61; post-publication corrections appear in red..
- [38] J. Renn and M. Schemmel (Eds.) (2007) The Genesis of General Relativity, Volume 3: Theories of Gravitation in the Twilight of Classical Physics, Between Mechanics, Field Theory, and Astronomy. Springer, Berlin. link1, link2 Cited by: 55.
- [39] (1993) Hyperbolic geometry on a hyperboloid. American Mathematical Monthly 100, pp. 442–455. Cited by: §2.
- [40] (2004) Relativistic velocity space, Wigner rotation, and Thomas precession. American Journal of Physics 72, pp. 943–960. Cited by: endnote 12.
- [41] (1986) David Hilbert on Poincaré, Klein, and the world of mathematics. Mathematical Intelligencer 8, pp. 75–77. Cited by: endnote 17.
- [42] (1995) The Hilbert Problems and the mathematics of a new century. Preprint–Reihe des Fachbereichs Mathematik 1. Cited by: §3.
- [43] (1968) Introduction to Special Relativity. McGraw-Hill, New York. Cited by: endnote 3.
- [44] A. Sommerfeld (Ed.) (1903) Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen V, Physik. Teubner, Leipzig. Cited by: §3.
- [45] (1909) Über die Zusammensetzung der Geschwindigkeiten in der Relativtheorie. Physikalische Zeitschrift 10, pp. 826–829. Cited by: §1, §2.
- [46] (1910) Zur Relativitätstheorie, I: Vierdimensionale Vektoralgebra. Annalen der Physik 337, pp. 749–776. Cited by: §3, endnote 9.
- [47] (1913) Anmerkungen zu Minkowski, Raum und Zeit. See Das Relativitätsprinzip; Eine Sammlung von Abhandlungen, Blumenthal, pp. 69–73. link1 Cited by: §4.
- [48] J. Stachel, D. C. Cassidy, J. Renn, and R. Schulmann (Eds.) (1989) The Collected Papers of Albert Einstein, Volume 2, The Swiss Years: Writings, 1900–1909. Princeton University Press, Princeton. link1 Cited by: §2, endnote 13.
- [49] (1986) Imagery in Scientific Thought by Arthur I. Miller. Mathematical Intelligencer 8 (2), pp. 65–74. Cited by: §1.
- [50] (1956) Relativity: The Special Theory. North-Holland, Amsterdam. Cited by: §3.
- [51] (1996) Relativity and Geometry. Dover Publications, New York. Cited by: endnote 16.
- [52] (1910) Anwendung der Lobatschefskijschen Geometrie in der Relativtheorie. Physikalische Zeitschrift 11, pp. 93–96. Cited by: §2.
- [53] (1999) Minkowski, mathematicians, and the mathematical theory of relativity. See The Expanding Worlds of General Relativity, Goenner et al., Einstein Studies, Vol. 7, pp. 45–86. link1 Cited by: §2, §2, §3, §3, endnote 14.
- [54] (1999) The non-Euclidean style of Minkowskian relativity. See The Symbolic Universe: Geometry and Physics, 1890–1930, Gray, pp. 91–127. link1 Cited by: §2, §3, endnote 8.
- [55] (2007) Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910. See The Genesis of General Relativity, Volume 3: Theories of Gravitation in the Twilight of Classical Physics, Between Mechanics, Field Theory, and Astronomy, Renn and Schemmel, pp. 193–252. link1, link2 Cited by: §1, §2, endnote 10, endnote 11.
- [56] S. A. Walter (Ed.) (2007) La correspondance d’Henri Poincaré, Volume 2: La correspondance entre Henri Poincaré et les physiciens, chimistes et ingénieurs. Birkhäuser, Basel. link1, link2 Cited by: endnote 17.
- [57] (2007) Poincaré, Jules Henri. See New Dictionary of Scientific Biography, Koertge, pp. 121–125. link1 Cited by: §1.
- [58] (2009) Hypothesis and convention in Poincaré’s defense of Galilei spacetime. See The Significance of the Hypothetical in the Natural Sciences, Heidelberger and Schiemann, pp. 193–219. link1, link2 Cited by: §1, §2, §2.
- [59] (1911) Relativitätsprinzip und Äther. Physikalische Zeitschrift 12, pp. 689–707, 737–758. Cited by: §3.
- [60] (1915) Die Mechanik im Rahmen der allgemeinen Physik. See Die Kultur der Gegenwart, Ihre Entwicklung und Ihre Ziele, 3, Mathematik - Naturwissenschaften - Medizin, 3, Anorganische Naturwissenschaften, 1: Physik, Hinneberg et al., pp. 1–78. Cited by: §3.
- [61] (1908) The theory of electricity. Bulletin of the American Mathematical Society 14, pp. 230–237. Cited by: §1.
Time-stamp: "21.07.2024 21:20"