Ether and electrons in relativity theory (1900–1911)
Published in Jaume Navarro, ed, Ether and Modernity,
67–87, Oxford:
Oxford University Press, 2018, doi 10.1093/oso/9780198797258.003.0005
Abstract
This chapter discusses the roles of ether and electrons in relativity theory. One of the most radical moves made by Albert Einstein was to dismiss the ether from electrodynamics. His fellow physicists felt challenged by Einstein’s view, and they came up with a variety of responses, ranging from enthusiastic approval, to dismissive rejection. Among the naysayers were the electron theorists, who were unanimous in their affirmation of the ether, even if they agreed with other aspects of Einstein’s theory of relativity. The eventual success of the latter theory (circa 1911) owed much to Hermann Minkowski’s idea of four-dimensional spacetime, which was portrayed as a conceptual substitute of sorts for the ether.
Introduction
The history of twentieth-century physics is scanned by the “classical”, or non-quantum theory of the electron, introduced by H. A. Lorentz, Joseph Larmor and others from the early 1890s. As a research program in physics, electron theory became more promising at the end of the decade, with the measurement of the electron mass-to-charge ratio in cathode-ray deflection experiments by J. J. Thomson and Emil Wiechert. It was successful in explaining magneto-optical phenomena, beginning with the Zeeman effect, and soon appeared to point the way to unifying the explanation of all forces – including the force of gravitation – by means of interactions between electrons and the ether. During the first two decades of the twentieth century, the physicists Lorentz, Henri Poincaré, Albert Einstein, Ebenezer Cunningham and Max Laue, all of whom were familiar with the idea of electromagnetic waves and electrons propagating in the ether, were led to engage with new technologies, mathematical formalisms and ideas about relative time and space. This chapter sketches some of the ways in which leading physicists sought to adapt pre-relativistic ether-based electron theories to the physics of relativity, from the emergence of the electromagnetic world-picture in 1900, to the publication of Emil Wiechert’s post-Minkowskian defense of the ether in 1911.
The history of the electron and that of the ether are tightly knit in the early twentieth century, although historians have paid much more attention to the former than the latter, leaving gaps in the literature concerning electron theory.11endnote: 1 The emergence of electron theory in the 1890s is described in a monograph by Buchwald (1985), while the development of electron theory has been studied in detail up to the time of Einstein’s and Poincaré’s theories of relativity (1905–1906) by Arthur I. Miller (1981), and Olivier Darrigol (2000). For the period up to 1920, works of reference include R. McCormmach (1970), B. Wheaton (1983), H. Kragh (2001), O. Knudsen (2001), W. Kaiser (2001), and J. Navarro (2012). Since E. T. Whittaker’s history of theories of “æther” and electricity (1953), historians of physics have considered the emergence of relativity theory in the context of ether and electron theory. A one-time participant in this history, Whittaker created a stir late in his life by attributing the theory of relativity not to Albert Einstein but to Lorentz and Poincaré. Much effort was subsequently expended to discredit Whittaker’s view and reinforce Einstein’s priority of discovery. The historian Stanley Goldberg, for example, argued that the theories of Poincaré and Einstein were distinct, except for the formalism (1970, 91). Many commentators since Goldberg have focused on the contrast between, on the one hand, Einstein’s provocative claim that the ether is a superfluous concept in electrodynamics and, on the other hand, Poincaré’s advocacy of an abstract ether.22endnote: 2 For a thoughtful review of the literature, see Darrigol (2004).
Most recently, Peter Galison showed that Poincaré and Einstein shared an interest in the topics of microphysics and clock synchronization (Galison 2003). For Galison, the emergence of relativity theory was the result of a chance confluence of three separate conceptual streams: physics, philosophy and technology. To these three streams I will add a fourth: applied mathematics, which Poincaré and Einstein brought into play in 1905, with profound and far-reaching consequences for conceptions of ether, electrons and relativity.
The first three streams came together in Leiden, in December, 1900. The occasion for this meeting was the jubilee celebration of Lorentz’s defense of his doctoral thesis; Poincaré had been invited to this celebration, along with one of his students and most of Europe’s electrodynamicists. Poincaré declined the invitation, but contributed a paper in which he analyzed the status of Newton’s third law in Lorentz’s electron theory.33endnote: 3 On Poincaré’s participation in the Lorentz Festschrift, see his correspondence with Heike Kamerlingh Onnes, published in Walter et al. (2016), docs. 2-63-1, 2-63-2, and 2-63-3..
1 Lorentz electrons and local time in Leiden
For purely mathematical reasons, Lorentz had introduced a fictive time which he called “Ortszeit” and which Poincaré called “temps local”, or local time, following the translation of his former student, Alfred Liénard (1898b). Poincaré realized that local time could be construed as a measurable quantity: local time is the time measured at relative rest by observers in uniform motion with respect to the ether, provided that they synchronize their watches in a certain way. The watches of the co-moving observers are synchronized, Poincaré explained, via an exchange of light signals, whereby light time-of-flight between observers is taken into account when zeroing the watches, but their common motion with respect to the ether is ignored (Poincaré 1900, 272).
Poincaré knew quite well that he was breaking new ground, as he described his time-synchronization protocol as a definition of local time. In providing this definition, Poincaré turned Lorentz’s electron theory into a regular theory of physics, that is, one having measurable consequences, whereas, before, it had been an abstract model. Lorentz seems not to have appreciated this point, although he thanked Poincaré for his contribution.44endnote: 4 See Lorentz to Poincaré, 20 January, 1901, in Walter et al. (2016, § 2-38-1). According to Lorentz (1895), the local time was a linear function of the ether time and the product of the distance and the frame velocity , divided by the square of the velocity of light in the ether, : . Lorentz noted that his formula was valid up to a first-order approximation in .
In addition to being a contribution to physics, Poincaré’s paper was a result of philosophical reflection on the nature of distant simultaneity, in relation to technical advances in astronomy and geodesy. As a member of the French Bureau of Longitudes, Poincaré was charged with the scientific oversight of national and colonial mapping projects, and French participation in international collaborations in astronomy and geodesy.
One of the latter projects sought to measure an arc of meridian passing through Peru, Ecuador and Colombia. Longitude measurement at the end of the nineteenth century involved several techniques, including that of fixing the position of celestial objects, and noting the temporal instant of astronomical events such as occultations and zenith passages. To determine the exact time of a given event, geodesists relied on time signals relayed by telegraph, as Poincaré observed in an original essay entitled “The measurement of time” (1898, English translation in Gould 2001, 220ff).
Poincaré’s essay on time measurement and his definition of local time both deeply influenced the later development of the principle of relativity, while Poincaré’s own conceptions evolved in the first years of the twentieth century, partly as a result of new ideas in electron theory, including those of Paul Langevin.
2 Langevin’s electron waves in ether
Paul Langevin’s theory of the electron drew on several sources, especially Joseph Larmor’s Æther and Matter (1900), J. J. Thomson’s Notes on Recent Researches (1893) and George Searle’s calculation of the energy of a Heaviside ellipsoid (Searle 1897). He introduced a distinction between the velocity fields and acceleration fields of the electron, and published a graphical depiction of the velocity waves of a spherical electron in motion. This led in turn to a geometrical derivation of the field of a Heaviside ellipsoid, introduced by Heaviside in 1889 and glossed by J. J. Thomson in 1893.
Langevin was concerned, as the title of his paper implies, with the source of electromagnetic radiation and the inertia of the electron. He supposed (following Larmor) that electron radiation was due entirely to acceleration, and he calculated thereby the energy of an electron in uniform motion. The “electromagnetic mass” of such an electron was given to be a function of the “wake” of the electron in motion, represented by Langevin’s velocity waves. The electron’s wake, in turn, depended on the charge distribution of the electron; Langevin considered uniform distributions by surface and volume.
Langevin’s distinction between velocity and acceleration waves recalled the retarded potentials introduced to electrodynamics by Langevin’s former teacher Henri Poincaré in the early 1890s, as well as the formulation of the potentials for a moving point charge due to Alfred Liénard (1898a) and Emil Wiechert (1900). Langevin’s theory, like all contemporary electron theories, assumed that his waves propagated in an ether at absolute rest. According to Langevin’s theory, electrons traveled through the ether at sublight velocity, generating velocity waves and, in the case of non-inertial motion, acceleration waves. These waves propagated in the ether with the speed of light; velocity waves dissipated rapidly, such that only acceleration waves could be detected far from the electron.55endnote: 5 For details on Langevin’s paper, see Miller (1973).
3 Poincaré on apparent time and the relativistic electron
As a student in the mid-1890s, Langevin had followed Poincaré’s lectures on Sommerfeld’s theory of diffraction, but he did not engage personally with Poincaré until September, 1904, when they were both members of the French delegation to the Congress of Arts and Sciences, held at the World’s Fair in St. Louis. The younger man was flattered by the attention of his former teacher, as he recounted the meeting by letter to his wife back in Paris.66endnote: 6 See Langevin’s notebook, box 123, and the letter to his wife of 26 September, 1904, box 3, Fonds Langevin, Library of l’École supérieure de physique et de chimie industrielle, Paris. By that time, the two men had a mutual interest in the theory of electrons, which was the topic of Langevin’s lecture in St. Louis (Langevin, 1906).
We do not know if Langevin discussed with Poincaré his forthcoming paper on the inertia of the electron, but we do know that Poincaré found inspiration from the latter paper for his discovery of the Lorentz group. Under the coordinate transformations of the Lorentz group, Poincaré demonstrated in 1905, the laws of electrodynamics retain their form. What impressed Poincaré most was not Langevin’s constant-volume model of the electron but his explanation of the velocity and acceleration waves produced by an electron: according to Langevin, these waves propagated in free ether at the speed of light. Instead of Langevin’s model, Poincaré preferred the deformable electron model proposed by Lorentz, as this model had the advantage, as Poincaré proved, of preserving the principle of relativity. Poincaré (1906, 149) noticed further that, by applying the Lorentz transformations to Langevin’s acceleration waves, he could recover Hertz’s solution of Maxwell’s equations for an oscillator at rest in the absolute ether.77endnote: 7 On Hertz’s solution, see Darrigol (2000, 251).
In June 1905, Poincaré supposed that all laws of physics were, likewise, form-invariant with respect to the transformations of the Lorentz group, including the law of gravitation. In a letter to Lorentz announcing his discovery, Poincaré observed that the requirement of Lorentzian form-invariance spelled the end of what he called the “unity of time” (Poincaré to Lorentz, ca. May, 1905, in Walter et al. 2016, § 2-38-3). Yet, Poincaré was not ready to abandon the traditional definition of time and space in this new theoretical context. He deftly elided the question of time and space deformation in his memoir on the dynamics of the electron (Poincaré 1906) by focusing on active transformations alone (Sternberg 1986).
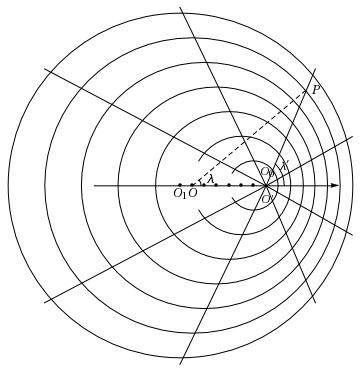
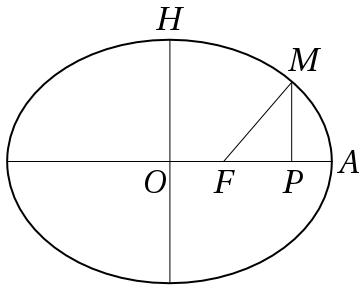
In his university lectures of 1906–1907, Poincaré explained how, in principle, one could measure Langevin waves and thereby determine the shape of an electromagnetic pulse generated by a source in motion with respect to the ether. According to lecture notes recorded by a student note-taker, Poincaré recalled Langevin’s paper and reproduced the latter’s schematic of an electron in motion (Fig. 1) along with a diagram of his own creation (Fig. 2), which showed how the electromagnetic pulse was related to the Lorentz transformations. The pulse created by the point source had the form of an ellipsoid, which was elongated in the direction of motion of the source and had a focus located at the source. A section through a meridian of the ellipsoid produces the ellipse shown in Fig. 2.
 |
Lorentz factor | |
| Semimajor axis | ||
| Semiminor axis | ||
| Eccentricity | ||
| Focal distance | ||
| Apparent time | ||
| Apparent displacement |
Poincaré’s diagram illustrates the Lorentz contraction, whereby all material objects contract by a Lorentz factor, but only in the direction of their motion with respect to the ether. Electromagnetic waves are immaterial, and are thereby unaffected by this contraction. If we measure the form of an electromagnetic pulse with a material rod at any instant of time, the result will depend on the speed of the rod with respect to the ether. For any nonzero rod velocity, the “true” form of the pulse is then an ellipsoid with an elongation proportional to the velocity of the measuring rod, assumed to be at relative rest with respect to the moving point source.
Poincaré’s ellipse was designed to explain the meaning of the primed variables appearing in the Lorentz transformations, which is to say, in Poincaré’s terminology, the “apparent” time and space coordinates of a reference frame moving uniformly with respect to the ether. While Poincaré affirmed the reality of Lorentz contraction of material bodies, he recoiled from affirming the corresponding reality of temporal deformation. According to student notes, he explained the situation as follows:
So Lorentz assumes that all bodies undergo a contraction in the direction of motion proportional to the square of velocity. Lengths are then altered, and durations are altered by the impossibility of setting watches truly, such that the apparent velocity of light is constant. (Vergne Notebook 2, 52)
Why did Poincaré feel it was impossible to “truly” synchronize mobile timekeepers in a state of relative rest? He did not explain this statement, but his intention is not hard to discern. Poincaré always referred to primed time and space coordinates of a reference frame in motion with respect to the ether as “apparent” coordinates, while the unprimed, “true” coordinates belonged to the frame of the absolute ether. In a manner consistent with this view, Poincaré’s discussion of the electromagnetic ellipse referred only to measurements made with rods and timekeepers at rest with respect to the ether, or to rods in motion, but not to timekeepers in motion. Thus, Poincaré had greater faith in mobile rods than in mobile clocks, even though the rods and clocks in physics laboratories and astronomical observatories around the world were all understood to be in motion with respect to extraterrestrial objects, for example, the center of the Sun. Poincaré was not alone in his distrust of mobile clocks in 1906, although he later had a change of heart, as explained in § 6.
4 Einstein exiles the light-ether
Even after relativity theory became a part of mainstream physics, Poincaré remained attached to the notion that the ether was a useful construct for the theorist. When he first affirmed that the laws of physics exhibit Lorentz covariance, electron theorists were agreed that the ether was an essential element of the physical world, with one exception: Albert Einstein. Shortly following Poincaré’s discovery of the Lorentz group, Einstein derived the Lorentz transformations from kinematic arguments, based on two postulates: the relativity of phenomena for inertial frames of motion, and the universal invariance of the speed of light in empty space. One consequence of Einstein’s theory, announced in the second paragraph of his essay “On the electrodynamics of moving bodies”, was that that the ether (or “light-ether”, in Einstein’s terms) was not needed in electrodynamics:
The introduction of a “light-ether” will prove to be superfluous, inasmuch as the view to be developed here will neither introduce an “absolutely resting space” endowed with special properties, nor associate a velocity-vector with a point of empty space at which electromagnetic processes occur.88endnote: 8 Einstein (1905b, 892), translation by the author. For line-by-line commentary on Einstein’s paper, see Miller (1981, 392), and Stachel (1989, Doc. 23).
Einstein’s remark was certainly designed to capture physicists’ attention, and so it did.
For a theory of the electrodynamics of moving bodies, refusing to assign a velocity to points of empty space where electromagnetic processes occur would have been an obvious non-starter. However, Einstein had figured out a way around this problem. The physicist needed only to describe electromagnetic processes in a frame with constant rectilinear velocity. Knowledge of the processes in all such frames was then obtained via the Lorentz transformations, which depend on the inter-frame velocity. All measurements are performed in inertial frames, and there is no recourse to an absolute frame of reference, or to a luminiferous ether.
Einstein’s decision to exile the ether from electrodynamics (and from physics in general) came at a high cost to what Poincaré referred to (see § 3) as the unity of time. While physicists at the turn of the twentieth century were familiar with the concept of the luminiferous ether, they were unfamiliar in general with the idea that time and space were relative notions.99endnote: 9 Notable exceptions include the Cambridge electron theorist Joseph Larmor, who remarked on the “difference of time reckoning” of orbiting electrons (see Larmor 1897, 229), and Poincaré, who gave an operational definition of local time (see Poincaré 1900, 272). Naturally, Einstein sought to render such ideas more plausible. The details of his arguments in favor of the relativity of time and space have been discussed by many authors, and need not be rehearsed here.1010endnote: 10 For a clear exposition of Einstein’s kinematics, see Martínez (2009). I will focus instead on how Einstein tried to persuade his readers of the logical compatibility of his two postulates.
The compatibility of Einstein’s postulates of relativity and light-speed invariance followed for Einstein from an argument which may be summarized as follows.1111endnote: 11 For a more detailed presentation see Walter (2018a). Let a spherical light wave be transmitted from the coordinate origin of two inertial frames designated and at time . In frame the light wave spreads with velocity such that the wavefront is expressed as
| (1) |
To obtain the equation of the wavefront in frame moving with velocity with respect to , we apply a certain linear transformation of coordinates from to , depending on a factor that depends on velocity.1212endnote: 12 Let this factor be , and coordinates in the frame be defined as: , , , , where , and the coordinate origins of the two frames are assumed to coincide. If we set , these transformations are equivalent to the Lorentz transformations. The result of the transformations, Einstein found, was just
| (2) |
Since (1) goes over to (2) via these transformations, Einstein observed, the light wave that is spherical in is also spherical in , it propagates with the same velocity , and consequently, “our two basic principles are mutually compatible” (Einstein 1905b, § 3, 901).
Einstein’s compatibility demonstration addressed one of the more immediate objections to be raised against his theory: that the propagation of light implied the existence of a substrate. This substrate, known as the ether, was common to the electron theories of Lorentz, Joseph Larmor, Alfred Bucherer, Paul Langevin and Max Abraham. Some, but not all of these theorists, went on to adopt relativity, but none of them ever saw fit to banish the luminiferous ether from physics.
5 Cunningham’s multiple ethers
Among British theorists, relativity theory had few proponents, if any, until Ebenezer Cunningham (1881–1977) took it up. A Cambridge-trained mathematician, senior wrangler in 1902, and lecturer in applied mathematics at University College London in 1907, Cunningham understood Einstein’s theory to be consistent with the existence of multiple ethers, provided that every inertial frame is associated with an ether.1313endnote: 13 See Goldberg (1970), and Hunt (1986). Inspired by Larmor’s electron theory, Cunningham’s multiple-ether approach to relativity recalls the mechanics proposed by the Leipzig mathematician Carl Neumann. Newton’s laws of mechanics, Neumann (1870) observed, give one the freedom to consider any inertial frame to be at rest with respect to a fixed set of coordinate axes he called the “Body Alpha”.1414endnote: 14 Cunningham (1912) recalled this fact, without mentioning Neumann. Views equivalent to Cunningham’s, but stripped of reference to the ether, were subsequently advanced by Minkowski (1909, 79) and Laue (1911, 33).
Cunningham’s first paper on relativity set out to overturn an objection raised by Max Abraham with respect to Lorentz’s electron theory. Abraham (1905, 205) believed that energy conservation required a fundamental modification of Lorentz’s deformable electron model, in the form of a supplemental internal and non-electromagnetic source of energy. Cunningham challenged Abraham’s (frame-dependent) definition of electromagnetic momentum, and found that, under the same quasi-stationary approximation, and an alternative momentum definition, the problem vanishes. He concluded that no non-electromagnetic energy was required by Lorentz’s electron model, which remained for him a possible foundation for a “purely electromagnetic theory of matter.”1515endnote: 15 Cunningham’s conclusion agrees with that reached later by Enrico Fermi; see Rohrlich (2007, 17), and Janssen & Mecklenburg (2006).
Along the way, Cunningham assumed that if Lorentz’s deformable electron is spherical when at rest, when put in motion and measured by comoving observers, it will remain spherical. But, when measured with respect to a frame at rest, the moving electron will have a “spheroidal shape as suggested by Lorentz” (Cunningham 1907, 540). Cunningham took this suggestion a step further, arguing that a light wave would appear spherical to all inertial observers, in agreement with Einstein on this point (and with reference to Einstein’s relativity paper of 1905).
Next, Cunningham took an important step toward the legitimation of the concept of light-sphere covariance, as Goldberg (1970, 114) first noticed. Einstein’s derivation of the Lorentz transformations could be reduced to a handful of steps, Cunningham realized, by requiring the covariance of the light-sphere equation (1) with respect to these transformations. Cunningham’s requirement of covariance of the light-sphere equation entailed the relativity of space and time:
For it is required, among other things, to explain how a light wave traveling outwards in all directions with velocity relative to an observer , may at the same time be traveling outwards in all directions with the same velocity relative to an observer moving relative to with velocity . This can clearly not be done without some transformation of the space and time variables of the two observers. (Cunningham 1907, 544)
Shortly after Cunningham’s derivation of the Lorentz transformations appeared in print, Einstein employed the same method of derivation, making Cunningham the first British contributor to what was later known as Einstein’s theory of relativity. However, Einstein did not acknowledge Cunningham as the source of the derivation, and he may well have come up with it on his own.1616endnote: 16 See Einstein (1908, § 3), reed. in Stachel (1989, Doc. 47). Cunningham’s paper appeared in the October 1907 issue of Philosophical Magazine, and Einstein’s review article was submitted for publication in Johannes Stark’s Jahrbuch der Radioaktivität und Elektronik on 4 December, 1907.
In subsequent years, Cunningham contributed to the generalization of the principle of relativity beyond frames with uniform motion, and published one of the first English-language textbooks on relativity. The latter work introduced Minkowski’s spacetime theory to English readers, and revived Cunningham’s earlier view of multiple mobile ethers, in a chapter entitled “Relativity and an Objective Æther”. The sufficient condition for the objective reality of the mobile ether was announced by Cunningham quite simply to be the conformity of its kinematics to those of the principle of relativity (Cunningham 1914, 193). Cunningham’s view of the mobile ether found employment throughout the 1920s, and well beyond Cambridge, thanks to Sommerfeld’s celebrated textbook Atombau und Spektrallinien (1919, 319) and its translations into French and English.
Contributing to Cunningham’s confidence in the universal validity of the principle of relativity was Minkowski’s spacetime theory, and also Einstein’s notion of light quanta, whereby light energy is not distributed uniformly in space but exists in discrete packets (Einstein 1905a). The theory of radiation appeared thereby to conform to relativity, at least by 1914, thanks in part to Einstein’s light quanta. Even before light quanta came to be accepted, the theory of radiation was central to discussions of relativity and the ether, as shown in the next section.
6 Relative time from radio waves
In the fall of 1908, the Göttingen mathematician David Hilbert (1862–1943) extended an invitation to Poincaré on behalf of the Wolfskehl Foundation to deliver a series of lectures. Poincaré accepted the honor, and delivered six lectures in Göttingen in April 1909, before an international audience of mathematicians and physicists.1717endnote: 17 For details on the lectures see Gray (2013), Rowe (2018), and Walter (2018b). One of Hilbert’s Göttingen colleagues, and perhaps his closest friend, was Hermann Minkowski (1864–1909), who had recently put forward the theory of spacetime. Minkowski’s spacetime theory borrowed key insights from Poincaré’s study of the Lorentz-covariant law of gravitation, including the idea of a four-dimensional vector space with one imaginary dimension. Minkowski had planned to pursue the theory, but following an attack of appendicitis, he died in January, 1909, just three months before Poincaré’s lecture series. There are indications that Minkowski’s theory inspired the topic of Poincaré’s final Wolfskehl lecture, which was entitled “The New Mechanics”, although the only Göttingen scientist mentioned by name in the published text of the lecture is the electron theorist Max Abraham, whom Poincaré characterized, along with H. A. Lorentz, as one of the “great demolitionists” of Newtonian mechanics (Poincaré 1910, 51).
One of the novelties of Minkowski’s theory was its definition of “proper time” as the parameter of a four-dimensional trajectory in spacetime, which was given to be the time read by an ideal clock describing this same trajectory. According to this theory, there are an infinite number of temporal axes, and as many corresponding three-dimensional spaces, which may be described with reference to a single spacetime extending infinitely in four dimensions. In Poincaré’s original scheme, as noted (§ 3), there was only one three-dimensional space – the ether – and one temporal dimension. Only clocks at rest in the ether were reliable timekeepers. But in Göttingen, Poincaré admitted that ideal clocks in motion with respect to the ether might also tell the right time.
The circumstances of this change are of interest, as they illustrate how technology can shake the foundations of science. Since Heinrich Hertz’s discovery of electromagnetic waves in air in the late 1880s, Poincaré had contributed to the theory of Hertzian waves, and engaged with the emerging technology of wireless telegraphy. When the Eiffel Tower was menaced with destruction, Poincaré backed a plan to employ it as the world’s tallest wireless transmission antenna (Galison 2003, 276), thereby strengthening the tower’s chances for preservation.
Poincaré knew that Hertzian waves propagate in the ether with the speed of light, . In his final Wolfskehl lecture, he imagined an observer in a vehicle in motion with respect to the ether with speed . Observer transmits telemetry data to an observer in a second vehicle moving with equal and opposite speed:
and begin by setting their watches, then sends telegrams to indicating his successive positions; putting these signals together, can give an account of ’s motion, and trace its curve. Well, the signals propagate at the speed of light; the watches marking apparent time vary at every instant and it will all go down as if ’s watch were fast. (Poincaré, 1910, 54-55)
As a result of the deformation of time revealed by the telemetry data, Poincaré explained a few months later, observer would come to believe his vehicle was advancing not at hyperlight velocity but at sublight velocity, so that the principle of relativity would not be violated (Poincaré, 1909, 173).
Notice that Poincaré’s watch in motion runs fast (with respect to a watch at rest in the ether), while Einstein’s clocks in motion run slow (with respect to clocks at relative rest). Not only is Einstein’s notion of relativistic time dilation readily admitted in physics, it also underpins the accuracy of global positioning systems.1818endnote: 18 Such systems correct for several motional effects, including special-relativistic time dilation, the latter effect being offset by gravitational blueshift; for a clear explanation, see Ashby (2002). What then are we to make of Poincaré’s fast watch? His thought experiment supposes that observer initially judges his speed relative to to be , in accordance with Newtonian kinematics. Only after exchanging telemetry data at the speed of light does revise his initial speed estimate downwards to a sub-light value. If we ignore Lorentz contraction, then time contraction is the only plausible means of obtaining a reduction to sub-light vehicle (and watch) velocity. Simply stated, observer concludes that his watch runs fast, because his speed is slower than Newtonian kinematics had led him to believe.1919endnote: 19 For a more detailed explanation, see Walter (2014).
As for Lorentz, by 1909 he, too, admitted that both rods and clocks in motion with respect to the ether could be used to measure temporal and spatial intervals, respectively. Like Poincaré, he recognized that inertial observers, whether in uniform motion or at rest, would agree on the speed of light, provided that the mobile clocks were optically synchronized in the frame of motion. Lorentz admitted the (Lorentz) contraction of bodies in their direction of motion, and proved that the apparent time of an observer in motion is just that indicated by the Lorentz transformations, such that time is apparently dilated in the observer’s frame of motion and, consequently, that his clocks run slower than identical clocks at rest in the ether. In his authoritative monograph The Theory of Electrons, Lorentz encouraged his reader to keep in mind that,
in doing all that has been said, the observer would remain entirely unconscious of his system moving (with himself) through the ether, and of the errors of his rod and his clocks. (Lorentz 1909, 226)
The “errors” of rod and clocks that Lorentz refers to are understood to be relative to the “true” values indicated by an identical rod and identical clocks at rest in the ether. From the foregoing considerations of Poincaré and Lorentz, we see that their attachment to the ether did not prevent them from admitting that time could be measured in moving frames. It was just not the true time.
7 Minkowskian electrons in spacetime
Since 1902, Hermann Minkowski had been a professor of mathematics in Göttingen, where he took up several topics in theoretical physics, including heat radiation and the electrodynamics of moving bodies. Before moving to Göttingen, Minkowski had been on the faculty of Zürich Polytechnic (currently ETH Zürich), where Albert Einstein and Mileva Marić were enrolled in his course in analysis.2020endnote: 20 Other students receiving grades from Minkowski included Louis Kollros, Marcel Grossmann, and Jacob Ehrat; undated autograph, Minkowski Papers, Jewish National and University Library. In Göttingen, Minkowski co-led a seminar on electron theory in the summer of 1905, in tandem with David Hilbert. Two years later, in the summer of 1907, Minkowski took notice of Einstein’s and Poincaré’s foundational contributions to relativity theory, and soon thereafter made a fundamental contribution of his own: the theory of spacetime.2121endnote: 21 On the electron-theory seminar, see Pyenson (1979); on Minkowski’s career in physics, see Walter (2008).
Minkowski presented his theory of spacetime in a lecture entitled “Space and Time” at the annual meeting of the German Association of Natural Scientists and Physicians in Cologne on 21 September, 1908. Central to his semi-popular lecture was a hand-colored transparency (Fig. 3). The transparency depicts two diagrams: on the left is a model of a two-dimensional Minkowski space and, on the right, a comparison of the trajectories in such a space of two electrons, with one at rest and the other in uniform motion. The transparency features several formulæ which illustrate Minkowski’s demonstration that the contraction of electrons (and Lorentz contraction in general) is a consequence of the fact that space and time are not separate entities, but part of a four-dimensional continuum: spacetime.
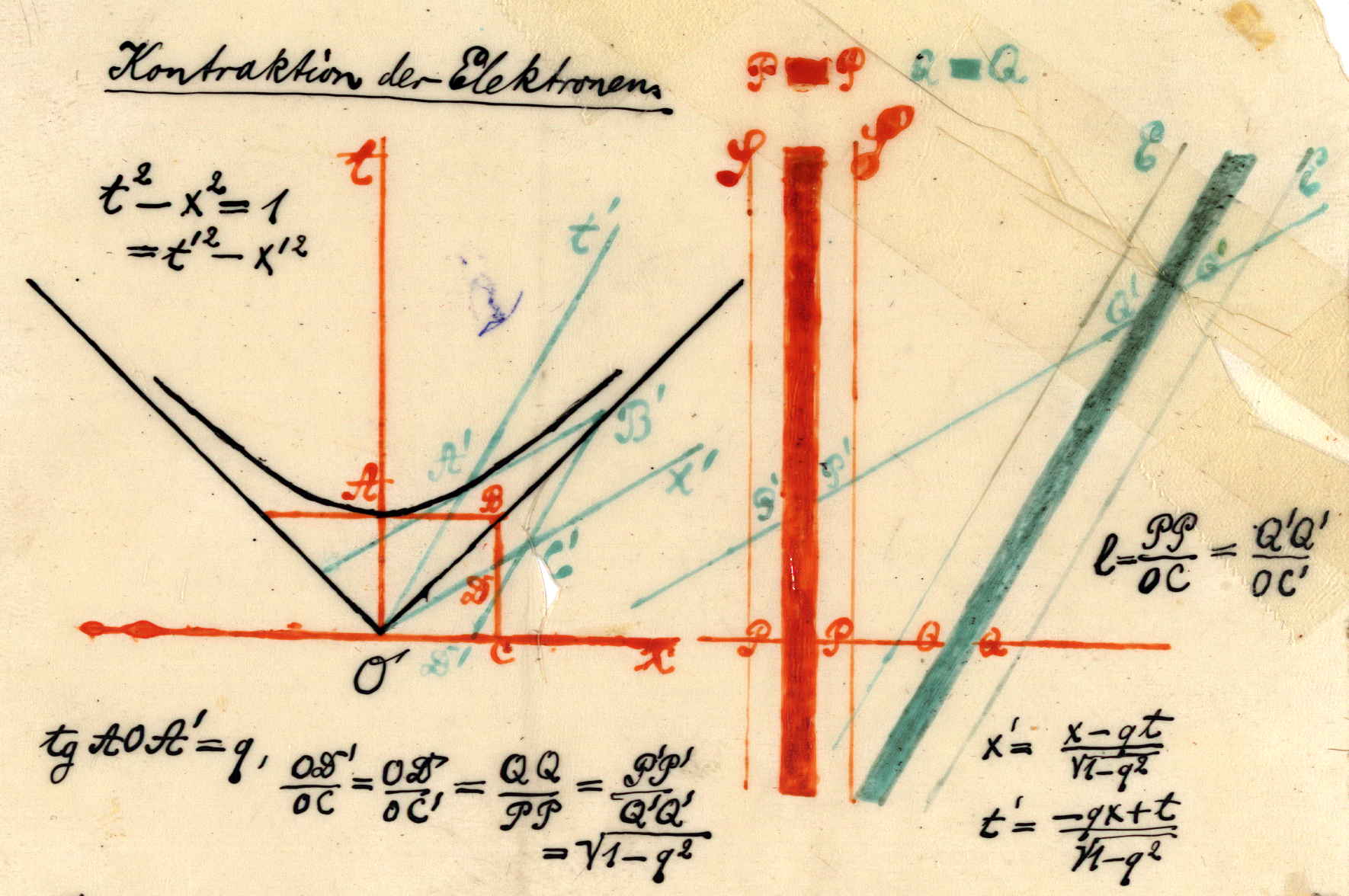
The transparency also shows that temporal intervals are dilated for observers in motion, although Minkowski appears not to have explained the details of the interpretation in Cologne. There can be little doubt about Minkowski’s recognition of the reality of time dilation, however, as he credited Einstein with “first clearly recognizing that the time of one electron is just as good as that of the other, which is to say, that and are to be treated identically” (Walter 1999). Minkowski thus sided with Einstein on the relative nature of time, rather than with Poincaré.
Minkowski did not take up the question of the form of an electromagnetic pulse for a source in motion, a topic earlier broached by Poincaré (see § 3), but his Cologne lecture carefully illustrated the Liénard-Wiechert potential on a three-dimensional spacetime diagram. In all of these considerations, Minkowski avoided reference to the luminiferous ether; he mentioned it only once, and then in a critical way, saying that the Lorentz contraction should not be thought of “as something like a consequence of ether drag” (Minkowski 1909, 80).
In Minkowski’s view, the ether constituted an obstacle to the general acceptance of his theory of spacetime. He thus concluded his Cologne lecture with an appeal to “those for whom the abolition of familiar views is unappealing or distressful”, suggesting in effect that, although the electromagnetic ether was no longer tenable in modern physics, four-dimensional spacetime was in fact the “true kernel of an electromagnetic world view” (Minkowski, 1909, 88). The idea that the electromagnetic world view could be pursued successfully by means of the spacetime theory was, at best, an instance of wishful thinking on Minkowski’s part but, as a rhetorical ploy, it effectively situated spacetime theory at the forefront of theoretical physics.
8 Minkowski spacetime as an ether stand-in
The pursuit of the electromagnetic world view implied a microphysical reduction and, for Minkowski, this reduction was to be carried out in the arena of four-dimensional spacetime. He was unable to advance this project very far himself, as he perished in January 1909, as previously mentioned. Other theorists stepped in to continue Minkowski’s research program, including his assistant in Göttingen, Max Born, and his boyhood friend, Arnold Sommerfeld, the professor of theoretical physics at the Ludwig-Maximilian University of Munich.
Both Born and Sommerfeld were instrumental to the success of spacetime theory among theoretical physicists. Most importantly in this respect, Sommerfeld reformulated Minkowski’s elegant but unfamiliar matrix calculus as a four-dimensional vector analysis, which appealed to physicists familiar with ordinary three-dimensional vector analysis. When presenting the latter formalism to readers of the Annalen der Physik, Sommerfeld formulated an argument that was implicit in Minkowski’s Cologne lecture (see § 7), to the effect that spacetime, or the “absolute world” in the Minkowskian vernacular, was a substitute for the ether:
The absolute world appears in place of the older theory, that is, the connection of space and time via the velocity of light , the immutability of which now constitutes the absolute substrate of electrodynamics. (Sommerfeld 1910, 749)
The “older theory” to which Sommerfeld refers here is that of Maxwell and Hertz, which assumed an ether at rest as the substrate of electromagnetic wave propagation with velocity in matter-free space. The immutability of the latter velocity was postulated by Einstein in 1905, as noted (in § 4), and also, in turn, by Minkowski, when he formulated the theory of spacetime.
In the years leading up to Minkowski’s discovery of spacetime, Sommerfeld had established his reputation as a leading electron theorist, and a critic of Einstein’s theory of relativity. The same was true of the Göttingen Privatdozent Max Abraham. A former doctoral student of Max Planck, Abraham was the author of an influential treatise on the electromagnetic theory of radiation. In the 1908 edition, which appeared shortly after Minkowski’s spacetime theory, Abraham adopted an approach midway between Sommerfeld’s enthusiastic embrace of Minkowskian relativity, and outright rejection of the principle of relativity.
For research in the electrodynamics of moving media, Abraham considered that both Lorentz’s theory and that of Minkowski represented attractive alternatives, provided that electrons were considered as point charges, in virtue of the ease of calculation these two theories offered. For electrons in empty space, on the other hand, Abraham felt that Lorentz’s theory was worthless. Not only was this theory inconsistent from a formal standpoint, in that it gave an improper value for electron rest mass (unless, like Poincaré, one admitted a non-electromagnetic binding potential), but it was also disconfirmed by Walter Kaufmann’s cathode-ray deflection experiments.
Earlier we saw how Poincaré had no truck with mobile clocks and preferred to keep time with clocks at rest in the ether (see § 3). Abraham shared this view with Poincaré, and consequently dismissed Einstein’s notion of path-dependent time, although he acknowledged that this was not ruled out by experiment. Time was absolute, in Abraham’s view, such that the difference between the rate of an ideal clock in motion and an equivalent clock at rest in the ether could be detected in principle, if not in practice. Space was also absolute for Abraham and, in light of the null result of the Michelson-Morley experiment (1887), he readily admitted that all material bodies contract in the direction of their motion with respect to the ether (Abraham, 1908, 368–369).
Both Sommerfeld and Abraham began to favor relativity following Minkowski’s contributions, and Alfred Bucherer’s experimental confirmation of the relativistic dynamics of charged particles. Sommerfeld argued that spacetime was a replacement for the ether, while Abraham devised an alternative to Minkowski’s relativistic theory of moving media, giving rise to over a century of debate over which formulation was to be preferred.2222endnote: 22 For an overview, see Ramos, Guillermo, and Obukhov (2011). The theory of moving media proposed by Abraham was no less relativistic than Minkowski’s theory. Yet, Abraham held that Einstein’s light postulate was incomprehensible without an ether, arguing that electromagnetic waves and fields could not subsist without a substrate (Abraham 1914).
Max Abraham was not alone in his rejection of Einstein’s relativity, not even in Göttingen. Walter Ritz (1878–1909) had been a former student of Minkowski in Zürich, a former doctoral student of Woldemar Voigt and, from 1909, a Privatdozent in Göttingen. Ritz found fault both with Einstein’s relativity, for its postulation of universal light-speed invariance, and with field theory in general. He also dismissed the ether in favor of an emission theory, which performed well in comparison to Lorentz’s electron theory, although it failed to account for the optics of moving bodies, including Fizeau’s demonstration that light propagation speed in running water changes with flow rate (Fizeau, 1851). Ritz’s theory of electrodynamics was even more radical than Einstein’s in some respects and, while Einstein paid attention to it, most physicists did not. When Ritz succumbed to tuberculosis in 1909, his theory died with him.2323endnote: 23 On Ritz’s contributions to electrodynamics see Martínez (2004) and Darrigol (2012).
While Ritz dismissed the luminiferous ether, Emil Wiechert sought to defend it. Director of the Göttingen Institute for Geophysics, Emil Wiechert was, like Ritz, unsatisfied with Einstein’s relativity. At the University of Königsberg in the 1890s, Wiechert developed a theory of charged particles which shared certain features of Lorentz’s theory, including an ether at rest. Unsurprisingly, Wiechert found much to admire in Lorentz’s electron theory and, like Lorentz, he felt that Einstein was wrong to do away with the ether. Along with many of his contemporaries, including Max Abraham (as previously mentioned), Wiechert felt that the electromagnetic field was not self-standing, but required a substrate. In addition, in his paper entitled “The Principle of Relativity and the Ether”, Wiechert deplored Einstein’s neglect of a model of electron shape and charge distribution, which meant for Wiechert that Einstein’s theory was not realistic, by default (Wiechert 1911, 748).
It is hard to imagine that Wiechert’s criticism would have bothered Einstein much. Unlike other electron theorists, Einstein neither needed nor offered a model of electron structure. Nonetheless, following Einstein’s own example, his contemporaries often referred to the “Lorentz-Einstein” theory, in virtue of a common recourse to the principle of relativity, and they considered the theories of Lorentz and Einstein to be empirically equivalent.
This conflation of theories may be explained by recalling a certain conceptual drift of the idea of ether among electrodynamicists, dating from the 1890s. There were those, like Henri Poincaré, who considered the ether to be real but undetectable in principle. Others, like Paul Drude, imagined that the properties of the electromagnetic field were actually properties of space, and not of the ether. And, while Poincaré and Drude both sought a microphysical reduction of electromagnetic phenomena, one theorist, Emil Cohn of the Kaiser-Wilhelm University of Strasbourg, eschewed both electrons and the ether in favor of a phenomenological theory featuring bare field equations, which compared well with that of Lorentz (Darrigol 2000, 366).
Wiechert’s criticism of relativity focused on the ether. The prospect of replacing the luminiferous ether with Minkowski spacetime did not please Wiechert, because spacetime seemed to him to allow bodies to propagate with velocities greater than the speed of light, while no such hyperlight phenomena had been observed. The possibility of hyperlight phenomena destroying the principle of relativity had been examined by Poincaré (1904), who noted that the propagation velocity of gravitational action had been calculated by Laplace to exceed the speed of light a million times over. Once Poincaré had discovered the Lorentz group, however, he showed that, if the speed of gravitation were equal to that of light, this would be no less consistent with astronomical observations than Newtonian gravitation. As one might guess, Wiechert’s defense of the ether did not mention Poincaré’s argument in favor of relativity.
Among those who admired Wiechert’s paper was the geodesist Friedrich Helmert, who cited it approvingly in his letter of nomination of Wiechert as a corresponding member of the Prussian Academy of Sciences; the letter was co-signed by Max Planck and Walther Nernst (Kirsten 1975, 198). One has to wonder how closely these scientists read Wiechert’s paper. In response to Wiechert’s article, Max Laue remarked the logical fallacy involved in deducing the existence of a class of preferred frames of motion (such as that of the luminiferous ether) from the inexistence of a different class of frames (in Wiechert’s case, frames with hyperlight velocity).
Laue went on to suggest that, in the absence of evidence for the existence of hyperlight phenomena, there was “no shame” in banning from physics further discussion of the existence of the ether and absolute time (Laue 1912). Seven years earlier, Einstein had deemed the ether superfluous to physics (as mentioned in § 4), but now Laue was recommending that the topic itself be censored, along with that of absolute time.
Educated in Berlin and Göttingen, Laue was, at the time of his critique of Wiechert’s view, a modest Privatdozent at the Ludwig-Maximilian University of Munich, attached to Sommerfeld’s Institute of Theoretical Physics. He had recently published the first German textbook on the principle of relativity (Laue 1911), and it soon became the standard work of reference in this domain. Six months after Laue pointed out the logical shortcomings of Wiechert’s defense of the ether, Sommerfeld communicated to the Munich Academy a paper written by Walter Friedrich, Paul Knipping and Laue on the interference of X-rays by crystals, a discovery for which Laue was awarded the Nobel Prize in Physics in 1914. That same year, Einstein became a member of the Prussian Academy of Sciences, on the strength of Planck’s letter of nomination, which emphasized Einstein’s revision of the notion of time and how this revision led to Minkowski’s spacetime theory (Kirsten 1975, 201). It is telling that Planck’s letter described Minkowski’s spacetime theory as a consequence of Einstein’s discoveries and that it neglected to mention Einstein’s criticism of the ether. Planck must have known that the members of the Prussian Academy were not ready to renounce the ether. The recognition of the two most vocal critics of the ether and absolute time – Laue and Einstein – by the Royal Swedish Academy of Sciences and the Prussian Academy of Sciences, respectively, sent a strong signal to physicists young and old that they, too, could do without the ether.
Yet, even among physicists who promoted the Einstein-Minkowski theory of relativity, Einstein and Laue’s anti-ether campaign met with resistance. As observed above, Sommerfeld and Max Abraham did not do away with the ether altogether. Likewise, when lecturing on the theories of Einstein, Minkowski, and Sommerfeld at the Collège de France in 1910–1911, Paul Langevin deplored Einstein’s view of the ether. Lecture notes by Léon Brillouin record Langevin’s remark on the subject: “The very notion of the ether loses its meaning, says Einstein – this is an exaggeration”. Langevin went on to point out that, while it is physically impossible to determine velocity with respect to the ether, “we can determine accelerations and rotations.”2424endnote: 24 Léon Brillouin, Notebook “Cours de Relativité au Collège de France 1910–1911”, Léon Brillouin Papers, Box 7, folder 8, American Institute of Physics, Niels Bohr Library.
9 Conclusion
When Einstein announced that his theory of the electrodynamics of moving bodies had no use for the luminiferous ether and that this ether was consequently “superfluous” to the theoretical domain of electromagnetism, he must have known it would capture the attention of his peers. And so it did, although few physicists were ready to banish talk of the ether from physics.
The electron-theoretical origins of relativity theory guided its development, even as new conceptual tools were brought into play. Poincaré’s discovery of the Lorentz group enabled him to reinterpret Langevin’s conception of velocity waves and acceleration waves propagating in the ether, and to recover Hertz’s demonstration of the production of electromagnetic waves by an oscillator. Such waves, he showed later, could be used to demonstrate in principle the deformation of temporal intervals for observers in frames of reference in motion with respect to the ether. The mechanism for this deformation remained mysterious, although, for Lorentz, at least, it was no more mysterious than the contraction of bodies in their direction of motion with respect to the ether. Both time dilation and length contraction issued from the same velocity-based modification of dynamical laws, in Lorentz’s view.
Directly opposed to the latter “dynamical” approach to relativity, Einstein’s relativistic kinematics had no need of an ether, and did not introduce one. Einstein took care, nonetheless, to provide an argument for the logico-mathematical compatibility of his twin postulates of relativity and universal light-speed invariance. This argument, as we have seen, did not convince electron theorists, including Lorentz, Poincaré, Max Abraham and Wiechert, to forgo the ether.
Soon after the theories of Poincaré and Einstein appeared on the scene, a third approach to relativity proved effective in attracting electron theorists, and many others besides, to the relativistic fold. Minkowski’s spacetime theory featured a powerful blend of ideas drawn from a variety of disparate sources, including Hertz’s theory of the electrodynamics of moving bodies; Lorentz-Poincaré electron theory; Einsteinian kinematics and the theory of continuous transformation groups. Where Einstein offered in exchange for the ether only a pair of postulates, the logical consistency of which was suspect, Minkowski and his followers proposed spacetime as a conceptual substitute.
From the fact that neither Einstein’s theory nor that of Minkowski found immediate success, it may be gathered that, in general, physicists did not find the idea of renouncing the ether to be particularly compelling. Nonetheless, most theoretical physicists adopted spacetime theory, including several theorists encountered in this chapter: Einstein, Cunningham, Abraham, Sommerfeld, Langevin and Lorentz. Many mathematicians, who had no prior attachment to the ether, joined them in this endeavor.2525endnote: 25 For quantitative details on the disciplinary reception of relativity theory, see Walter (1999).
By the end of the first decade of the twentieth century, relativity and spacetime theory were poised to dominate theoretical physics. To some extent, the rise of these theories came at the expense of ether theories, which continued nonetheless to appeal to theorists like Wiechert. The Lorentz-Poincaré electron theory survived the onslaught of relativity, via mathematical reformulation and conceptual adaptation to the principle of relativity. In a lecture delivered in Salzburg in September 1909, Einstein remarked that Lorentz’s theory was the only electron theory that was useful and had clear foundations (McCormmach 1970, 79). By the end of 1911, however, electron theory was seen to be incapable of explaining black-body radiation. This incapacity was not due to the theory’s fixed-ether foundation but rather on its assumption that bodies emit and absorb energy continuously (Kuhn 1978, 134).
Acknowledgments: I am grateful to the Dibner Library of the History of Science and Technology for granting me a residence in November, 2016, and to the Niedersächsiche Staats- und Universitätsbibliothek Göttingen for authorizing publication of the diagram in Figure 3.
Notes
- 1 The emergence of electron theory in the 1890s is described in a monograph by Buchwald (1985), while the development of electron theory has been studied in detail up to the time of Einstein’s and Poincaré’s theories of relativity (1905–1906) by Arthur I. Miller (1981), and Olivier Darrigol (2000). For the period up to 1920, works of reference include R. McCormmach (1970), B. Wheaton (1983), H. Kragh (2001), O. Knudsen (2001), W. Kaiser (2001), and J. Navarro (2012).
- 2 For a thoughtful review of the literature, see Darrigol (2004).
- 3 On Poincaré’s participation in the Lorentz Festschrift, see his correspondence with Heike Kamerlingh Onnes, published in Walter et al. (2016), docs. 2-63-1, 2-63-2, and 2-63-3..
- 4 See Lorentz to Poincaré, 20 January, 1901, in Walter et al. (2016, § 2-38-1). According to Lorentz (1895), the local time was a linear function of the ether time and the product of the distance and the frame velocity , divided by the square of the velocity of light in the ether, : . Lorentz noted that his formula was valid up to a first-order approximation in .
- 5 For details on Langevin’s paper, see Miller (1973).
- 6 See Langevin’s notebook, box 123, and the letter to his wife of 26 September, 1904, box 3, Fonds Langevin, Library of l’École supérieure de physique et de chimie industrielle, Paris.
- 7 On Hertz’s solution, see Darrigol (2000, 251).
- 8 Einstein (1905b, 892), translation by the author. For line-by-line commentary on Einstein’s paper, see Miller (1981, 392), and Stachel (1989, Doc. 23).
- 9 Notable exceptions include the Cambridge electron theorist Joseph Larmor, who remarked on the “difference of time reckoning” of orbiting electrons (see Larmor 1897, 229), and Poincaré, who gave an operational definition of local time (see Poincaré 1900, 272).
- 10 For a clear exposition of Einstein’s kinematics, see Martínez (2009).
- 11 For a more detailed presentation see Walter (2018a).
- 12 Let this factor be , and coordinates in the frame be defined as: , , , , where , and the coordinate origins of the two frames are assumed to coincide. If we set , these transformations are equivalent to the Lorentz transformations.
- 13 See Goldberg (1970), and Hunt (1986).
- 14 Cunningham (1912) recalled this fact, without mentioning Neumann.
- 15 Cunningham’s conclusion agrees with that reached later by Enrico Fermi; see Rohrlich (2007, 17), and Janssen & Mecklenburg (2006).
- 16 See Einstein (1908, § 3), reed. in Stachel (1989, Doc. 47). Cunningham’s paper appeared in the October 1907 issue of Philosophical Magazine, and Einstein’s review article was submitted for publication in Johannes Stark’s Jahrbuch der Radioaktivität und Elektronik on 4 December, 1907.
- 17 For details on the lectures see Gray (2013), Rowe (2018), and Walter (2018b).
- 18 Such systems correct for several motional effects, including special-relativistic time dilation, the latter effect being offset by gravitational blueshift; for a clear explanation, see Ashby (2002).
- 19 For a more detailed explanation, see Walter (2014).
- 20 Other students receiving grades from Minkowski included Louis Kollros, Marcel Grossmann, and Jacob Ehrat; undated autograph, Minkowski Papers, Jewish National and University Library.
- 21 On the electron-theory seminar, see Pyenson (1979); on Minkowski’s career in physics, see Walter (2008).
- 22 For an overview, see Ramos, Guillermo, and Obukhov (2011).
- 23 On Ritz’s contributions to electrodynamics see Martínez (2004) and Darrigol (2012).
- 24 Léon Brillouin, Notebook “Cours de Relativité au Collège de France 1910–1911”, Léon Brillouin Papers, Box 7, folder 8, American Institute of Physics, Niels Bohr Library.
- 25 For quantitative details on the disciplinary reception of relativity theory, see Walter (1999).
References
- Theorie der Elektrizität 2: Elektromagnetische Theorie der Strahlung. Teubner, Leipzig. External Links: Link Cited by: §5.
- Theorie der Elektrizität 2: Elektromagnetische Theorie der Strahlung. Teubner, Leipzig. External Links: Link Cited by: §8.
- Die neue Mechanik. Scientia (Rivista di Scienza) 15, pp. 8–27. External Links: Link Cited by: §8.
- Relativity and the Global Positioning System. Physics Today 55, pp. 41–47. Cited by: endnote 18.
- Mathematical Correspondences and Critical Editions. Springer, Cham. External Links: Document Cited by: S. A. Walter (2018b).
- Histories of the Electron: The Birth of Microphysics. MIT Press, Cambridge MA. External Links: Document Cited by: W. Kaiser (2001), O. Knudsen (2001), H. Kragh (2001).
- From Maxwell to Microphysics. University of Chicago Press, Chicago. External Links: Link Cited by: endnote 1.
- On the electromagnetic mass of a moving electron. Philosophical Magazine 14, pp. 538–547. External Links: Link Cited by: §5, §5.
- The principle of relativity. Report–British Association 81, pp. 236–245. External Links: Link Cited by: endnote 14.
- The Principle of Relativity. Cambridge University Press, Cambridge. External Links: Link Cited by: §5.
- Electrodynamics from Ampère to Einstein. Oxford University Press, Oxford. External Links: Link Cited by: §8, endnote 1, endnote 7.
- The mystery of the Einstein-Poincaré connection. Isis 95 (4), pp. 614–626. Cited by: endnote 2.
- Electrodynamics in the physics of Walther Ritz. See Le destin douloureux de Walther Ritz (1878–1909), physicien théoricien de génie, Pont, Cahiers de Vallesia, Vol. 45, pp. 207–240. Cited by: endnote 23.
- Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. Annalen der Physik 322 (6), pp. 132–148. Cited by: §5.
- Zur Elektrodynamik bewegter Körper. Annalen der Physik 322, pp. 891–921. External Links: Link Cited by: §4, endnote 8.
- Relativitätsprinzip und die aus demselben gezogenen Folgerungen. Jahrbuch der Radioaktivität und Elektronik 4, pp. 411–462. Cited by: endnote 16.
- Sur les hypothèses relatives à l’éther lumineux, et sur une expérience qui paraît démontrer que le mouvement des corps change la vitesse avec laquelle la lumière se propage dans leur intérieur. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 33 (13), pp. 349–355. External Links: Link Cited by: §8.
- Einstein’s Clocks and Poincaré’s Maps: Empires of Time. Norton, New York. Cited by: §6, Introduction.
- The Expanding Worlds of General Relativity. Birkhäuser, Boston/Basel. Cited by: S. A. Walter (1999).
- In defense of Ether: the British response to Einstein’s special theory of relativity 1905–1911. Historical Studies in the Physical Sciences 2, pp. 89–125. Cited by: §5, Introduction, endnote 13.
- The Value of Science: Essential Writings of Henri Poincaré. Random House, New York. Cited by: §1.
- Henri Poincaré: A Scientific Biography. Princeton University Press, Princeton. External Links: Link Cited by: endnote 17.
- On the electromagnetic effects due to the motion of electrification through a dielectric. Philosophical Magazine 27 (167), pp. 324–339. Cited by: §2.
- Interactions: Mathematics, Physics and Philosophy, 1860–1930. Springer, Dordrecht. Cited by: M. Janssen and M. Mecklenburg (2006).
- Experimenting on the ether: Oliver J. Lodge and the great whirling machine. Historical Studies in the Physical Sciences 16 (1), pp. 111–134. External Links: Link, Document Cited by: endnote 13.
- From classical to relativistic mechanics: electromagnetic models of the electron. See Interactions: Mathematics, Physics and Philosophy, 1860–1930, Hendricks et al., pp. 65–134. Cited by: endnote 15.
- Electron gas theory of metals: free electrons in bulk matter. See Histories of the Electron: The Birth of Microphysics, Buchwald and Warwick, pp. 255–304. Cited by: endnote 1.
- Physiker über Physiker: Wahlvorschläge zur Aufnahme von Physikern in die Berliner Akademie 1870 bis 1929. Akademie-Verlag, Berlin. Cited by: §8, §8.
- O.W. Richardson and the electron theory of matter, 1901–1916. See Histories of the Electron: The Birth of Microphysics, Buchwald and Warwick, pp. 227–254. Cited by: endnote 1.
- The electron, the protyle, and the unity of matter. See Histories of the Electron: The Birth of Microphysics, Buchwald and Warwick, pp. 195–226. Cited by: endnote 1.
- Black-Body Theory and the Quantum Discontinuity, 1894–1912. University of Chicago Press, Chicago. Cited by: §9.
- Sur l’origine des radiations et l’inertie électromagnétique. Journal de physique théorique et appliquée 4, pp. 165–183. External Links: Link Cited by: Figure 1.
- The relations of the physics of electrons to the other branches of science. See Congress of Arts and Science: Universal Exposition, St. Louis, 1904, Rogers, pp. 121–156. External Links: Link Cited by: §3.
- A dynamical theory of the electric and luminiferous medium; Part 3. Philosophical Transactions of the Royal Society A 190, pp. 205–300. Cited by: endnote 9.
- Æther and Matter. Cambridge University Press, Cambridge. External Links: Link Cited by: §2.
- Das Relativitätsprinzip. Vieweg, Braunschweig. External Links: Link Cited by: §5, §8.
- Zwei Einwände gegen die Relativitätstheorie und ihre Widerlegung. Physikalische Zeitschrift 13, pp. 118–120. Cited by: §8.
- Champ électrique et magnétique produit par une charge concentrée en un point et animée d’un mouvement quelconque. Éclairage électrique 16, pp. 5–14, 53–59, 106–112. External Links: Link Cited by: §2.
- La théorie de Lorentz et celle de Larmor (I). Éclairage électrique 16 (34), pp. 320–334. External Links: Link Cited by: §1.
- Versuch einen Theorie der elektrischen und optischen Erscheinungen in bewegten Körpern. Brill, Leiden. External Links: Link Cited by: endnote 4.
- The Theory of Electrons and its Application to the Phenomena of Light and Radiant Heat. Columbia University Press, New York. External Links: Link Cited by: §6.
- Ritz, Einstein, and the emission hypothesis. Physics in Perspective 6, pp. 4–28. Cited by: endnote 23.
- Kinematics: The Lost Origins of Einstein’s Relativity. Johns Hopkins University Press, Baltimore. Cited by: endnote 10.
- Einstein, Lorentz, and the electron theory. Historical Studies in the Physical Sciences 2, pp. 41–87. External Links: Link Cited by: §9, endnote 1.
- On the relative motion of the earth and the luminiferous ether. American Journal of Science 34, pp. 333–345. External Links: Link Cited by: §8.
- A study of Henri Poincaré’s ‘Sur la dynamique de l’électron’. Archive for History of Exact Sciences 10 (3), pp. 207–328. External Links: Link, Document Cited by: endnote 5.
- Albert Einstein’s Special Theory of Relativity: Emergence (1905) and Early Interpretation. Addison-Wesley, Reading, MA. Cited by: endnote 1, endnote 8.
- Raum und Zeit. Jahresbericht der deutschen Mathematiker-Vereinigung 18, pp. 75–88. External Links: Link Cited by: §5, §7, §7.
- A History of the Electron: J. J. and G. P. Thomson. Cambridge University Press, Cambridge. Cited by: endnote 1.
- Ueber die Principien der Galilei-Newton’schen Theorie. Teubner, Leipzig. External Links: Link Cited by: §5.
- La mesure du temps. Revue de métaphysique et de morale 6, pp. 1–13. External Links: Link Cited by: §1.
- La théorie de Lorentz et le principe de réaction. Archives néerlandaises des sciences exactes et naturelles 5, pp. 252–278. External Links: Link Cited by: §1, endnote 9.
- L’état actuel et l’avenir de la physique mathématique. Bulletin des sciences mathématiques 28, pp. 302–324. External Links: Link Cited by: §8.
- Sur la dynamique de l’électron. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 140, pp. 1504–1508. External Links: Link Cited by: §3.
- Sur la dynamique de l’électron. Rendiconti del Circolo matematico di Palermo 21, pp. 129–176. External Links: Link, Document Cited by: §3, §3.
- La mécanique nouvelle. Revue scientifique 47-2 (6), pp. 170–177. External Links: Link Cited by: §6.
- Sechs Vorträge über ausgewählte Gegenstände aus der reinen Mathematik und mathematischen Physik. Teubner, Leipzig/Berlin. External Links: Link Cited by: §6, §6.
- Le destin douloureux de Walther Ritz (1878–1909), physicien théoricien de génie. Vallesia, Sion. Cited by: O. Darrigol (2012).
- Physics in the shadow of mathematics: the Göttingen electron-theory seminar of 1905. Archive for History of Exact Sciences 21 (1), pp. 55–89. External Links: Link Cited by: endnote 21.
- Relativistic analysis of the dielectric Einstein box: Abraham, Minkowski and total energy-momentum tensors. Physics Letters A 375 (16), pp. 1703–1709. Cited by: endnote 22.
- Congress of Arts and Science: Universal Exposition, St. Louis, 1904. Houghton, Mifflin, Boston/New York. External Links: Link Cited by: P. Langevin (1906).
- Classical Charged Particles. World Scientific, Singapore. Cited by: endnote 15.
- Beyond Einstein: Perspectives on Geometry, Gravitation, and Cosmology in the Twentieth Century. Birkhäuser, New York. External Links: Document Cited by: S. A. Walter (2018a).
- A Richer Picture of Mathematics: the Göttingen Tradition and Beyond. Springer, Cham. Cited by: endnote 17.
- On the steady motion of an electrified ellipsoid. Philosophical Magazine 44, pp. 329–341. External Links: Link Cited by: §2.
- Zur Relativitätstheorie, I: Vierdimensionale Vektoralgebra. Annalen der Physik 337, pp. 749–776. Cited by: §8.
- Atombau und Spektrallinien. Vieweg, Braunschweig. Cited by: §5.
- The Collected Papers of Albert Einstein, Volume 2, The Swiss Years: Writings, 1900–1909. Princeton University Press, Princeton. External Links: Link Cited by: endnote 16, endnote 8.
- Imagery in Scientific Thought by Arthur I. Miller. Mathematical Intelligencer 8 (2), pp. 65–74. Cited by: §3.
- Notes on Recent Researches in Electricity and Magnetism: Intended as a Sequel to Professor Clerk-Maxwell’s Treatise on Electricity and Magnetism. Clarendon, Oxford. External Links: Link Cited by: §2.
- Minkowski, mathematicians, and the mathematical theory of relativity. See The Expanding Worlds of General Relativity, Goenner et al., Einstein Studies, Vol. 7, pp. 45–86. External Links: Link Cited by: §7, endnote 25.
- Hermann Minkowski’s approach to physics. Mathematische Semesterberichte 55 (2), pp. 213–235. External Links: Link, Document Cited by: endnote 21.
- Poincaré on clocks in motion. Studies in History and Philosophy of Modern Physics 47 (1), pp. 131–141. External Links: Link, Document Cited by: endnote 19.
- Henri Poincaré Papers. http://henripoincarepapers.univ-nantes.fr, Nantes. External Links: Link Cited by: §3, endnote 3, endnote 4.
- Figures of light in the early history of relativity (1905–1914). See Beyond Einstein: Perspectives on Geometry, Gravitation, and Cosmology in the Twentieth Century, Rowe et al., Einstein Studies, Vol. 14, pp. 3–50. External Links: Link, Document Cited by: endnote 11.
- Poincaré-week in Göttingen, in light of the Hilbert-Poincaré correspondence of 1908–1909. See Mathematical Correspondences and Critical Editions, Borgato et al., pp. 297–310. External Links: Link, Document Cited by: endnote 17.
- The Tiger and the Shark: Empirical Roots of Wave-Particle Dualism. Cambridge University Press, Cambridge. External Links: Link Cited by: endnote 1.
- A History of the Theories of Aether and Electricity, Volume 2: The Modern Theories, 1900–1926. T. Nelson, London. External Links: Link Cited by: Introduction.
- Elektrodynamische Elementargesetze. In Recueil de travaux offerts par les auteurs à H. A. Lorentz, J. Bosscha (Ed.), Archives néerlandaises des sciences exactes et naturelles, Vol. 5, pp. 549–573. Cited by: §2.
- Relativitätsprinzip und Äther. Physikalische Zeitschrift 12, pp. 689–707, 737–758. Cited by: §8.