Figures of Light in the Early History of Relativity
(1905–1914)
Published in David Rowe, Tilman Sauer, and Scott A. Walter,
eds, Beyond
Einstein: Perspectives on Geometry, Gravitation, and Cosmology in
the Twentieth Century (Einstein Studies 14), 3–50, Basel:
Birkhäuser, 2018; doi: 10.1007/978-1-4939-7708-6_1
Abstract
Albert Einstein’s bold assertion of the form-invariance of the equation of a spherical light wave with respect to inertial frames of reference (1905) became, in the space of six years, the preferred foundation of his theory of relativity. Early on, however, Einstein’s universal light-sphere invariance was challenged on epistemological grounds by Henri Poincaré, who promoted an alternative demonstration of the foundations of relativity theory based on the notion of a light ellipsoid. A third figure of light, Hermann Minkowski’s lightcone also provided a new means of envisioning the foundations of relativity. Drawing in part on archival sources, this paper shows how an informal, international group of physicists, mathematicians, and engineers, including Einstein, Paul Langevin, Poincaré, Hermann Minkowski, Ebenezer Cunningham, Harry Bateman, Otto Berg, Max Planck, Max Laue, A. A. Robb, and Ludwig Silberstein, employed figures of light during the formative years of relativity theory in their discovery of the salient features of the relativistic worldview.
1 Introduction
When Albert Einstein first presented his theory of the electrodynamics of moving bodies (1905), he began by explaining how his kinematic assumptions led to a certain coordinate transformation, soon to be known as the “Lorentz” transformation. Along the way, the young Einstein affirmed the form-invariance of the equation of a spherical light-wave (or light-sphere covariance, for short) with respect to inertial frames of reference. The introduction of the notion of a light sphere in this context turned out to be a stroke of genius, as Einstein’s idea resonated with physicists and mathematicians, and provided a way to understand the Lorentz transformation, kinematics, simultaneity, and Lorentz-covariance of the laws of physics.
A focus on the light sphere as a heuristic device provides a new perspective on the reception of relativity theory, and on the scientific community’s identification of Einstein as the theory’s principal architect. Acceptance of relativity theory, according to the best historical accounts, was not a simple function of having read Einstein’s paper on the subject.11endnote: 1 For gradualist views of the acceptance of relativity theory see Hirosige (1968), Miller (1981), and Darrigol (1996, 2000). A detailed understanding of the elements that turned Einsteinian relativity into a more viable alternative than its rivals is, however, not yet at hand. Likewise, historians have only recently begun to investigate how scientists came to recognize Einstein as the author of a distinctive approach to relativity, both from the point of view of participant histories (Staley 1998), as well as from that of disciplinary history (Walter 1999a). The latter studies underline the need for careful analysis when evaluating the rise of Einstein’s reputation in the scientific community, in that this ascent was accompanied by that of relativity theory itself.
We know, for example, that the fortunes of relativity theory improved when A. H. Bucherer (1908a) announced the results of electron-deflection experiments in line with relativist predictions. Einstein’s most influential promoter, Max Planck, himself a founder of relativistic dynamics, was in Einstein’s view largely responsible for the attention paid by physicists to relativity theory (Heilbron 1986, 28). Planck also praised Hermann Minkowski’s four-dimensional approach to relativity, the introduction of which marked a turning-point in the history of relativity (Walter 1999a). There is more than Planck’s praise to tie Einstein’s theory of relativity to Minkowski’s spacetime theory. Much as the lightcone distinguishes Minkowski’s theory from earlier theories of space and time, the light sphere was one of the key objects that set apart Einstein’s theory of relativity (as it became known around 1911) from alternative theories of the electrodynamics of moving bodies.
My account begins with Einstein’s relativity paper of 1905, in which the notion of the form-invariance of the equation of a light sphere was introduced. While interest in form-invariance of the differential equation of light-wave propagation dates from the 1880s, the idea that a light sphere remains a light sphere for all inertial observers – with a universal velocity of light – was recognized as a major conceptual innovation in the fall of 1907, when it was first used to derive the Lorentz transformation. By then, the light sphere had already been employed in Paris by Henri Poincaré, along with a second figure of light, the “light ellipsoid”, to illustrate an alternative to Einsteinian kinematics. Inspired by his readings of Einstein and Poincaré, Minkowski identified and exploited a third figure of light, the “lightcone”, to define and illustrate the structure of spacetime. In the wake of spacetime theory, other investigators used figures of light to explore the relation of simultaneity, the properties of four-vectors, and the conformal structure of spacetime. The period of study comes to a close with the publication of Ludwig Silberstein’s textbook on relativity, which was the first to feature all three figures of light. Although light-figures sparked discussion and debate until the early 1920s, Silberstein’s discussion represents a point of closure on this topic, by bringing together previously-disjoint intellectual developments of the previous decade.
By following light-figures through a selection of published and archival sources during the period 1905–1914, the skills and concerns of a nascent community of relativists are brought into focus. The progress of this community’s knowledge of the scope, history and foundation of relativity theory, as it related to the domains of measurement theory, kinematics, and group theory is reflected in the ways it put these new objects to use, by means of accounts both formal and discursive in nature. During the formative years of relativity, an informal, international, and largely independent group of physicists, mathematicians, and engineers, including Einstein, Paul Langevin, Poincaré, Minkowski, Ebenezer Cunningham, Harry Bateman, Otto Berg, Max Planck, Max Laue, Arthur A. Robb, and Ludwig Silberstein, employed figures of light to discover salient features of the relativistic worldview. Their contributions, and those of their critics, are considered here on their own merits, as part of an intellectual movement taking place during a period when the meaning of the theory of relativity was still negotiable, and still being negotiated.
2 Einstein’s light sphere
The concepts of relative time and relative simultaneity were taken up by Einstein in the course of his relativity paper of 1905. It seems he was then unaware of Lorentz’s (1904) attempt to demonstrate the form-invariance of Maxwell’s equations with respect to the Lorentz transformation. By 1904, the Lorentz transformation had appeared in several journals and books (Darrigol 2000, 381). Einstein demonstrated the covariance of Maxwell’s equations with respect to the Lorentz transformation, but the requirement of covariance of Maxwell’s equations itself determines the transformations only up to a global factor (assuming linearity). Consequently, in order to derive the Lorentz transformation, imagination was required in order to set this factor equal to unity.
To this end, Lorentz (1904) advanced arguments of a physical nature, which failed to convince Henri Poincaré. If the transformation in question is to form a group, Poincaré argued, the troublesome factor can be assigned no value other than unity. Einstein took a different tack: for him, the determination of the global factor resulted from neither physical nor group-theoretical considerations, but from kinematic assumptions.22endnote: 2 On the assumption of linearity, see Brown (2005, 26), and for the kinematic background to Einstein’s first paper on relativity, see Martínez (2009). Einstein did not let kinematics decide the matter once and for all in 1905. In a letter of September 1918 written to his friend, the anti-relativist and political assassin Friedrich Adler, Einstein considered the global factor in the Lorentz transformation to be of an empirical nature, whose value had been determined (to Einstein’s satisfaction) by the results of certain electron-deflection experiments (Walter 2009, 213). Poincaré expressed his views to Lorentz by letter in May 1905; see Walter, Bolmont, and Coret, eds, 2007b, §§ 38.4, 38.5.
He embarked upon what Martínez (2009, § 7) describes as a “tortuous” algebraic derivation of the Lorentz transformation from his kinematic assumptions, which puzzled contemporary scientists and modern historians alike. The details of Einstein’s derivation have been the subject of close attention, and need not be rehearsed here. Instead, I will focus on Einstein’s insertion of an argument for the compatibility of his twin postulates of relativity and light-speed invariance.33endnote: 3 On the compatibility argument, see Williamson (1977). Gaps in Einstein’s reasoning are apparent from a modern standpoint; see, for example, Kennedy (2005).
The compatibility of Einstein’s postulates of relativity and light-speed invariance followed for Einstein from an argument which may be summarized (in slightly-updated notation) as follows. Let a spherical light-wave be transmitted from the coordinate origin of two inertial frames designated and at time . In system the light-wave spreads with velocity such that the wavefront is expressed as:
| (1) |
To obtain the equation of the wavefront in frame moving with velocity with respect to , we apply a transformation of coordinates from to , depending on an as-yet-undetermined factor , which is a function of :
| (2) |
where . Applying (2) to (1), Einstein found:
| (3) |
Since (1) goes over to (3) via the transformation (2), Einstein observed, the light-wave that is spherical in is also spherical in , propagates with the same velocity , and consequently, “our two basic principles are mutually compatible” (Einstein 1905, § 3, 901).
Einstein’s compatibility demonstration addressed one of the more immediate objections to be raised against his theory: that the propagation of light implied the existence of a substrate. This substrate, known as the ether, was common to the electron theories of Lorentz, Larmor, Bucherer-Langevin, and Abraham. Einstein’s axiomatic approach to the electrodynamics of moving bodies did not destroy the conviction that a substrate was required for light propagation. On the contrary, Einstein’s twin postulates of relativity and lightspeed invariance rendered his theory all the more suspect. Arnold Sommerfeld, for example, was impressed by Einstein’s “genial” theory, but worried that something “almost unhealthy lies in this unconstruable and intuition-free dogma”.44endnote: 4 Sommerfeld to H.A. Lorentz, 26 Dec. 1907, in Kox, ed. (2008, § 165). For Richard Tolman (1910, 28, n. 1), Einstein’s light postulate expressed “seemingly contradictory ideas” of relativity and independence of propagation velocity of light from that of its source.
Tolman’s concern over the compatibility of Einstein’s postulates stemmed in part from the fact that the propagation velocity of light is an extraordinary velocity in Einstein’s kinematics. While a spherical light-wave is form-invariant for inertial frames in Einstein’s scheme, the form of other physical objects is frame-dependent. A rigid sphere of matter with radius at rest in frame , for example, is judged by an observer in motion along the -axis to have the flattened form of an ellipsoid of revolution with axes . Light-waves had a special role to play in Einstein’s theory, being essentially different from other physical objects. As Einstein put it, the speed of light in his theory “plays the role of an infinitely great speed”, and it renders “senseless” the notion of hyperlight velocities (Einstein 1905, § 4, 903).
How did Einstein’s compatibility argument for his postulates of relativity and constant lightspeed sit with his contemporaries? At least one of Einstein’s readers, the Cambridge-trained mathematician Ebenezer Cunningham (1881–1977) was intrigued by Einstein’s approach. A student of St. John’s College, where his director of studies was the influential analytic geometer H. F. Baker, Cunningham was Senior Wrangler in 1902.55endnote: 5 For an assessment of Baker’s rise to prominence among Cambridge geometers, see Barrow-Green and Gray (2006). Cunningham lectured on mathematics in Liverpool from 1904, and was joined there in 1906 by another Senior Wrangler (1903), Harry Bateman (1882–1946), who had studied at Trinity College. In 1907, Cunningham left Liverpool to lecture on applied mathematics at University College London, and in 1911, he returned to St. John’s as a Fellow and lecturer in mathematics.66endnote: 6 See McCrea (1978), and John Heilbron’s interview with Cunningham (1963).
Among British theorists, relativity theory had few proponents, if any, when Cunningham first took it up.77endnote: 7 A proponent of Einstein’s theory is understood here to be an individual seeking either to support or to extend any of the novel ideas contained in Einstein’s 1905 paper. On the British reception of relativity, see Goldberg (1970), Sánchez-Ron (1987), and Warwick (2003). Cunningham naturally read Einstein in his own fashion, drawing on the intellectual tools at his disposal. He understood Einstein’s theory to be consistent with the existence of multiple ethers, provided that every inertial frame is associated with an ether.88endnote: 8 See Goldberg (1970), and Hunt (1986). Inspired by Larmor’s electron theory,99endnote: 9 Cunningham noted a personal communication with Larmor, to the effect that while a proof of the Lorentz transformation’s validity for electron theory to second order of approximation in appeared in the latter’s Æther and Matter (1900), Larmor had “known for some time that [the Lorentz transformation] was exact” (Cunningham 1907, 539). Cunningham’s multiple-ether view of relativity recalls the view of mechanics proposed by the Leipzig mathematician Carl Neumann. Newton’s laws of mechanics, Neumann observed, give one the freedom to consider any inertial frame to be at rest with respect to a fixed set of coordinate axes he called the “Body Alpha”.1010endnote: 10 Cunningham (1912) recalled this fact, without mentioning Neumann. Neumann described the role assumed by the Body Alpha in the general theory of motion to be similar to that of the luminiferous ether in the theory of optical phenomena (Neumann, 1870, 21). Views equivalent to Cunningham’s, but stripped of reference to the ether, were subsequently advanced by Minkowski (1909, 79) and Laue (1911a, 33). Cunningham’s view, based on multiple ethers, found employment throughout the 1920s, thanks to Sommerfeld’s celebrated textbook Atombau und Spektrallinien (1919, 319).
Cunningham’s first paper on relativity set out to overturn an objection raised by Max Abraham with respect to Lorentz’s electron theory. Abraham (1905, 205) believed that energy conservation required a fundamental modification of Lorentz’s deformable electron model, in the form of a supplemental internal, non-electromagnetic source of energy. Cunningham challenged Abraham’s (frame-dependent) definition of electromagnetic momentum, and found that, under the same quasistationary-motion approximation, and an alternative momentum definition, the problem vanishes. He concluded that no non-electromagnetic energy was required by Lorentz’s electron model, which remained for him a possible foundation for a “purely electromagnetic theory of matter.”1111endnote: 11 Cunningham’s conclusion agrees with that reached later by Fermi; see Rohrlich (2007, 17), Janssen and Mecklenburg (2006).
Along the way, Cunningham assumed that if Lorentz’s deformable electron is spherical when at rest, when put in motion and measured by comoving observers, it will remain spherical. But when measured with respect to a frame at rest, the moving electron will have a “spheroidal shape as suggested by Lorentz” (Cunningham 1907, 540). Cunningham took this suggestion a step further, arguing that a light-wave would appear spherical to all inertial observers, in agreement with Einstein on this point (and with reference to Einstein’s relativity paper of 1905).
Next, Cunningham took an important step toward the legitimation of the concept of light-sphere covariance, as Goldberg (1970, 114) first noticed. Einstein’s demonstration of the Lorentz transformation could be reduced to a handful of steps, Cunningham realized, by requiring the covariance of the light-sphere equation (3) with respect to this transformation. Cunningham’s requirement of covariance of the light-sphere equation entailed the relativity of space and time:
For it is required, among other things, to explain how a light-wave traveling outwards in all directions with velocity relative to an observer , may at the same time be traveling outwards in all directions with the same velocity relative to an observer moving relative to with velocity . This can clearly not be done without some transformation of the space and time variables of the two observers. (Cunningham 1907, 544)
Cunningham went on to observe that Alfred Bucherer’s recent calculation of electron mass (Bucherer 1907) was mistaken, because Bucherer did not “take into account this necessary modification of coordinates”.1212endnote: 12 Cunningham (1907, 547). Both Cunningham and Planck failed to understand Bucherer’s theory, which allowed for closed links between electrons; see Darrigol (2000, 371). Unconvinced by Cunningham’s lesson, Bucherer (1908b) retorted quite rightly that light-sphere covariance was not required for the explanation of “any known fact of observation.”1313endnote: 13 According to Balàsz (1972), Bucherer’s remark shows that he was “confused about the basic problem of relativity”, in that he failed to “realize the connection of this problem with the Michelson-Morley experiment and its relation to the transformation laws.” Yet the Lorentz-FitzGerald contraction explains on its own the null result of the Michelson-Morley experiment, as Bucherer and contemporary theorists knew quite well.
Bucherer’s complaint of inutility notwithstanding, Cunningham’s clever and economical approach to deriving the Lorentz transformation represented a significant advance over Einstein’s cumbersome approach via ideal rods and clocks, although he did not realize at first just what he had accomplished. This much may be gathered from his response to Bucherer’s complaint, published in March 1908:
May I explain that I did not wish to assert that [light-sphere covariance] was required by any known fact of observation, but that I took it to be involved in the statement of the principle. I may have read more into it more than was intended, but if the Maxwell equations are assumed to hold when referred, as occasion requires, to various frames of reference moving relatively to one another, the deduction cannot be escaped that the velocity of propagation of a spherical wave will be found to be exactly the same, whatever the frame of reference.
With Bucherer’s insistent prompting, Cunningham recognized not only that lightspeed invariance was a convention, but that he had freely interpreted Einstein’s theory.
A few months after Cunningham’s original paper appeared, Einstein employed the latter’s method in an invited review of relativity theory, making Cunningham the first British contributor to what was later known as Einstein’s theory of relativity. Einstein did not acknowledge Cunningham’s proof, however, and he may well have come up with it on his own.1414endnote: 14 See Einstein (1908, § 3); reed. in Stachel et al., eds. (1989, vol. 2, Doc. 47). Cunningham’s paper appeared in the October 1907 issue of the Philosophical Magazine, and Einstein’s review article was submitted for publication in Johannes Stark’s Jahrbuch der Radioaktivität und Elektronik on 4 December 1907.
Further contributions to relativity from Cunningham and Bateman, making novel use of the light sphere, were still to come in 1908–1909. Before examining this work (in § 8), it will be useful to review first the light-figures produced by Poincaré and Minkowski, whose four-dimensional approach to relativity provided the basis for the later papers of Cunningham and Bateman.
3 Poincaré and the Lorentz group
Poincaré (1905b) was quick to grasp the idea that the principle of relativity could be expressed mathematically by transformations that form a group. This fact had several immediate consequences for Poincaré’s understanding of relativity. Notably, following a method outlined by Lie & Scheffers (1893, 669), Poincaré identified invariants of the Lorentz transformation directly from the fact that the transformation is a rotation about the coordinate origin in four-dimensional space (with one imaginary axis). Any transformation of the Lorentz group, he noted further, may be decomposed into a dilation and a linear transformation leaving invariant the quadratic form , where light velocity is rationalized to unity. Poincaré naturally associated this quadratic form with the propagation of light, and gravitational action (Poincaré 1906, §§ 4, 8).
Curiously for one who had engaged with the Riemann-Helmholtz-Lie problem of space, Poincaré avoided drawing consequences for the foundations of geometry from the “new mechanics” of the Lorentz group, with one exception. He observed that while previously, measurement of length implied the physical displacement of solids considered to be rigid,
…this is no longer true in the current theory, if we admit the Lorentzian contraction. In this theory, two equal lengths, by definition, are two lengths spanned by light in the same lapse of time. (Poincaré, 1906, 132)
Light signals, in other words, were the new basis for both temporal and spatial measurement. But how was one to go about measuring lengths in a frame in motion, where measuring rods are Lorentz-contracted?
Poincaré’s measurement problem called for a solution, and shortly, Poincaré provided one.1515endnote: 15 An alternative approach, advanced by Max Born (1909), involved redefining the notion of a rigid body in Minkowski spacetime. On related developments, see Maltese and Orlando (1995). In lectures at the Sorbonne in 1906–1907, he interpreted the Lorentz transformation with respect to a geometric figure representing the wavefront of an electromagnetic pulse, as judged by an observer at rest with respect to the ether. I will refer to Poincaré’s figure as a “light ellipsoid”, following Sommerfeld’s coinage, and to a meridional section of this ellipsoid as a “light ellipse”.1616endnote: 16 Sommerfeld insisted in his lectures on electrodynamics that a Lorentz transformation does not change a “Lichtkugel” into a “Lichtellipsoid” (Sommerfeld 1948, 236). The light ellipse is a staple of Poincaré’s kinematics of relativity, in that he illustrated his view with this device on at least four occasions, with significant variations, during the final six years of his life, from 1906 to July 12, 1912. His light ellipse theory appeared three times in print during Poincaré’s lifetime, in French journals of popular science, and in a book of philosophy of science.1717endnote: 17 See the edition of Henri Vergne’s notes of Poincaré’s 1906–1907 lectures at the Paris Faculty of Science (Chopinet, 1953), and his 1912 lectures at the École supérieure des postes et télégraphes (Poincaré 1913), along with the two articles (Poincaré 1908a, 1909). The article of 1908 was reedited by Poincaré in Science et méthode (1908b); the light ellipse is described on p. 239, but the diagram was suppressed from this version, presumably by the editor, Gustave Le Bon.
The origin of Poincaré’s light ellipse is uncertain, but his most likely source of inspiration is a paper published by Paul Langevin in March 1905. Before discussing the latter source, however, another possible source should be mentioned: Einstein’s relativity paper. As noted above, Einstein clearly expressed the spherical form of a light shell for inertial observers, and used the invariance of this form under certain coordinate transformations to show the compatibility of his postulates of relativity and lightspeed invariance. Also, Einstein made an implicit distinction between an abstract geometric surface and the realization of such a surface by wavefronts as measured by inertial observers. This distinction underlies Einstein’s analysis (1905, § 8) of the energy content of a given “light-complex” (Lichtkomplex) as measured in two inertial frames. Einstein imagined light propagating spherically in a frame , and examined the form of the surface obtained by setting to zero the time in the transformed wave equation. The volume enclosed by the resulting “ellipsoidal surface” (Ellipsoidfläche) measured in is greater than that enclosed by the corresponding “spherical surface” (Kugelfläche) measured in , such that the energy density is less in than in .
Einstein’s focus in section 8 of his paper was on the energy content of volumes delimited by spherical and ellipsoidal surfaces. I disagree in this instance with Arthur Miller’s gloss of Einstein’s argument, inasmuch as Miller identifies Einstein’s equation for the ellipsoidal surface as an “ellipsoidal light pulse” (Miller 1981, 310). What Einstein wrote with respect to the equation in question was the following: “Die Kugelfläche ist – in bewegten System betrachtet – eine Ellipsoidfläche …” (Einstein 1905, § 8). In other words, Einstein considered the energy content of an ellipsoid, and not an ellipsoidal light pulse.
More than likely, some of Einstein’s contemporaries also misread Einstein’s remarks on the Ellipsoidfläche in a moving frame, and imagined an ellipsoidal light shell in a moving frame. For example, in 1912, the French polymath Maurice Lémeray (1860–1926), a recognized expert on relativity theory and a former warship designer, confidently attributed a light ellipse interpretation to Einstein, only to retract his view shortly thereafter.1818endnote: 18 See Lémeray (1912), communicated to the Paris Academy of Sciences on 9 December, 1912, and the retraction (ibid., p. 1572). It is not clear whether Lémeray meant to attribute a flattened light-ellipsoid or an elongated light-ellipsoid to Einstein. Several years later, the Swiss physicist Édouard Guillaume (1921) referred to an “ellipsoïde de Poincaré”. Guillaume corresponded with Einstein on this topic; see Kormos Buchwald (2006, Doc. 241). While we can not rule out the possibility that Einstein’s Kugelfläche inspired Poincaré’s light ellipse, there is a second source, which is directly linked to Poincaré’s research on relativity: a paper by Paul Langevin. In the next section, I present an argument in favor of Langevin’s influence on Poincaré’s conception of the light ellipse.
4 Langevin’s electron wake
Paul Langevin (1872–1946) was a former student of Poincaré, whose 1896 lectures at the Paris Faculty of Sciences on Sommerfeld’s theory of diffraction he followed.1919endnote: 19 See Langevin’s notes of Poincaré’s lectures, Fonds Langevin, box 123, Bibliothèque de l’École supérieure de physique et de chimie industrielle, Paris. Langevin had also studied at the Cavendish Laboratory, and his novel theory of the electron drew on several sources, especially Joseph Larmor’s Æther and Matter (1900), J. J. Thomson’s Notes on Recent Researches (1893), and George Searle’s calculation of the energy of a Heaviside ellipsoid (Searle 1897). He introduced a distinction between the velocity fields and acceleration fields of the electron, and published a graphical depiction of the velocity waves of a spherical electron in motion. This led in turn to a geometrical derivation of the field of a Heaviside ellipsoid, introduced by Heaviside in 1889, and glossed by J. J. Thomson in 1893 (op. cit.).
Langevin was concerned, as the title of his paper suggests, with the source of electron radiation and the inertia of the electron. He supposed that electron radiation was due entirely to acceleration. This stipulation allowed him to calculate the energy of an electron in uniform motion. The “electromagnetic mass” of such an electron was given to be a function of the “sillage”, or wake of the electron in motion. The wake was composed of “velocity waves” propagating, in Langevin’s picturesque language, “like the waves emanating from the front of a ship” (Langevin 1905, 171). The electron’s electromagnetic mass thus depended on the postulated charge distribution of the electron; Langevin considered both a uniform surface charge, and a uniform volume charge.
The distinction between velocity and acceleration waves made here by Langevin recalls the retarded potentials introduced to electrodynamics by his former teacher Henri Poincaré (1891), following Lorenz (1867). It recalls as well the formulation of the potentials for a moving point charge due to Alfred Liénard (1898) and Emil Wiechert (1900). Langevin’s theory, like Lorentz’s electron theory, assumed an ether at absolute rest. According to Langevin, electrons traveled through the ether at velocities less than that of light, generating velocity waves and, in the case of non-inertial motion, acceleration waves. Both sorts of waves propagated in the ether with the speed of light, while velocity waves dissipated rapidly, such that only acceleration waves could be detected far from the electron.2020endnote: 20 For details on Langevin’s paper, see Miller (1973).
5 Poincaré’s light ellipse
As a student in the mid-1890s, Langevin had followed Poincaré’s lectures on Sommerfeld’s theory of diffraction, but he did not engage personally with Poincaré until September, 1904, when they were both members of the French delegation to the Congress of Arts and Sciences, held at the World’s Fair in Saint Louis. The younger man was flattered by the attention of his former teacher, as he recounted the meeting by letter to his wife back in Paris.2121endnote: 21 See Langevin’s notebook, box 123, and letter to his wife of 26 September, 1904, box 3, Fonds Langevin, Library of the École supérieure de physique et de chimie industrielle, Paris. By that time, the two men had a mutual interest in the theory of electrons, which was the topic of Langevin’s lecture in Saint Louis (1906).
We do not know if Langevin ever discussed with Poincaré his forthcoming paper on the inertia of the electron (Langevin, 1905). However, we do know that Poincaré found inspiration from the latter paper for his discovery of the Lorentz group, as it is one of the few papers cited by Poincaré (along with Lorentz, 1904). Under the coordinate transformations of the Lorentz group, Poincaré demonstrated in 1905, the laws of electrodynamics retain their form. What impressed Poincaré most was not Langevin’s constant-volume model of the electron, but his explanation of the velocity and acceleration waves produced by an electron, according to which these waves propagate in free ether at the speed of light. Instead of Langevin’s model, Poincaré preferred the deformable electron model proposed by Lorentz, which had the advantage, as Poincaré proved, of preserving the principle of relativity. Poincaré (1906, 149) noticed further that by applying the Lorentz transformations to Langevin’s acceleration waves, he could recover Hertz’s solution of Maxwell’s equations for an oscillator at rest in the absolute ether.2222endnote: 22 On Hertz’s solution, see Darrigol (2000, 251).
In June, 1905, Poincaré supposed that all laws of physics were likewise form-invariant with respect to the transformations of the Lorentz group, including the law of gravitation. In a letter to Lorentz announcing his discovery, Poincaré observed that the requirement of Lorentzian form-invariance spelled the end of what he called the “unity of time” (Poincaré to Lorentz, in Walter 2016, 2-38-3). Yet Poincaré was not ready to abandon the traditional definition of time and space in this new theoretical context. He deftly elided the question of time and space deformation in his memoir on the dynamics of the electron (Poincaré 1906) by focusing on active transformations alone (Sternberg 1986).
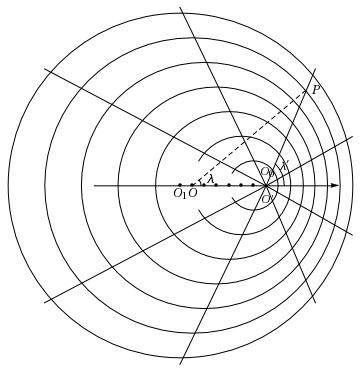
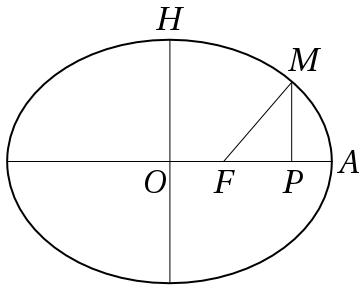
Questions of relativity of space and time remained on Poincaré’s mind after 1905. In his university lectures of 1906–1907, Poincaré explained how, in principle, one could measure Langevin waves, and thereby determine the shape of an electromagnetic pulse generated by a source in motion with respect to the ether. According to lecture notes by a student note-taker, Henri Vergne (1879–1943), Poincaré recalled Langevin’s paper, and reproduced (Fig. 3) the latter’s illustration of the waves produced by an electron in motion (Fig. 1).2323endnote: 23 Henri Vergne, notebook 2, CAPHI, University of Nantes. He also produced a diagram of his own creation (Fig. 2), which showed how an electromagnetic pulse was related to the Lorentz transformations. The pulse created by the point source had the form of an ellipsoid, elongated in the direction of motion of the source, with a focus colocated at the source. A section through a meridian of the ellipsoid produces the ellipse shown in Fig. 2.
 |
Lorentz factor | |
| Semimajor axis | ||
| Semiminor axis | ||
| Eccentricity | ||
| Focal distance | ||
| Apparent time | ||
| Apparent displacement |
Poincaré’s diagram illustrates the Lorentz contraction, whereby all material objects contract by a Lorentz factor, but only in the direction of their motion with respect to the ether. Commentators offer conflicting views of other aspects of Poincaré’s ellipse, and as I will show later, Poincaré himself changed his view of the ellipse around 1909.
Poincaré’s concrete model of the propagation of electromagnetic waves from a source in uniform motion merits our attention for two reasons. His light ellipse was, first of all, a graphical illustration of kinematic relations in relativity theory, the first in a long line of such techniques designed to display the relations of relativistic kinematics. Secondly, Poincaré’s theory of the light ellipse stands as the first of many attempts by physicists to reconcile an assumed Lorentz-covariance of physical laws with Galilean kinematics. In particular, Poincaré’s interpretation of the Lorentz transformation constrasts sharply with the views of Cunningham and Einstein, outlined in previous sections.
The light ellipse is, at the same time, a curious historical object, that has given rise to variant readings. To some extent, the lack of consensus among historians is to be expected: none of Poincaré’s four independent discussions of the light ellipse clarifies fully his protocol for measuring the dimensions of the locus of light in a moving frame. To help distinguish the various readings of Poincaré’s ellipse, let us consider three propositions:
-
1.
The principle of relativity is valid.
-
2.
Measurements of the light shell are performed with concrete rods by observers at relative rest with respect to rods and clocks, at an instant of apparent time indicated by light-synchronized clocks.
-
3.
Measurements of the light shell are performed with concrete rods in motion by observers at relative rest with respect to the clocks, at an instant of absolute time .
Einsteinian relativity upholds (1) and (2) only, provided that we neglect the distinction made in (2) between “apparent time” and “absolute time”, time and space being frame-dependent quantities in Einstein’s view.
The first historically-motivated account of Poincaré’s light ellipse, due to Cuvaj, accepts (2), but rejects (1), in that comoving observers “will have contracted measuring sticks, in their own frame too, so that a wave-sphere (of radius ) will appear as an ellipsoid” (Cuvaj 1970, 74, original emphasis). Thus for Cuvaj, Poincaré’s protocol contradicts the principle of relativity, and in light of this contradiction, it is “defective”.
An alternative reconstruction of Poincaré’s measurement protocol, advanced by Susan Wright (1975, 453), and Olivier Darrigol, accepts (1) and (3), such that Poincaré’s light ellipse “represents the location of a light pulse at a given value of the absolute time and for geometers belonging to a moving system” (Darrigol 1995, 41). Both Wright and Darrigol find Poincaré’s approach to be circuitous in comparison to that of Einstein. For Darrigol, Poincaré’s employment of kinematic attributes from different frames appeared “an absurdity from the Einsteinian point of view” (Darrigol 1995, 41), although he later acknowledged that Einstein, too, mixed his attributes on occasion (Darrigol, 2015, n. 67).
According to the reading suggested here, following Walter (2014), Poincaré originally upheld (1) and (3), but later revised his view, discarding (3) in favor of (2). Poincaré, like Einstein, considered light propagation in empty space to be the only physical phenomenon not subject to Lorentz contraction. In his first popular account of relativity theory, Poincaré (1907) drew a series of consequences for the philosophy of phenomenal space, during which he invoked a thought-experiment, which proceeds as follows. Let all objects undergo the same expansion overnight; in the morning, the unsuspecting physicist will not notice any change. Poincaré likened the fantasy of an overnight spatial expansion to the relativity of moving bodies in contemporary physics, in that Lorentz’s theory admitted the contraction of bodies in their direction of motion with respect to the ether. Just as with the thought-experiment, Poincaré disallowed detection of the contraction, from the assumption that instruments of measure exhibit compensating effects.2424endnote: 24 Poincaré’s fantasy was extended by Richard Tolman (1914) via dimensional analysis, in the form of a “principle of similitude”, a view that attracted sharp criticism from Percy Bridgman (1916).
In the same vein, Poincaré admitted the principle of observational equivalence among inertial observers. He retained, however, a semantic distinction between true and apparent quantities, corresponding respectively to quantities measured in a frame at absolute rest , and those measured in frames in uniform motion with respect to the absolutely-resting frame.2525endnote: 25 The notion of an absolutely-resting frame remained an abstraction for Poincaré. In 1912, he upheld the conventionality of spacetime, and expressed a preference for Galilei spacetime over Minkowski spacetime (Walter 2009). His definition of temporal and spatial intervals for observers in uniform motion with respect to the ether went as follows: apparent time (or equivalently, local time) is the time indicated by light-synchronized clocks at relative rest; local distance is measured by light time-of-flight, such that a concrete rod at rest with apparent unit length in a direction parallel to that of frame motion has true length .
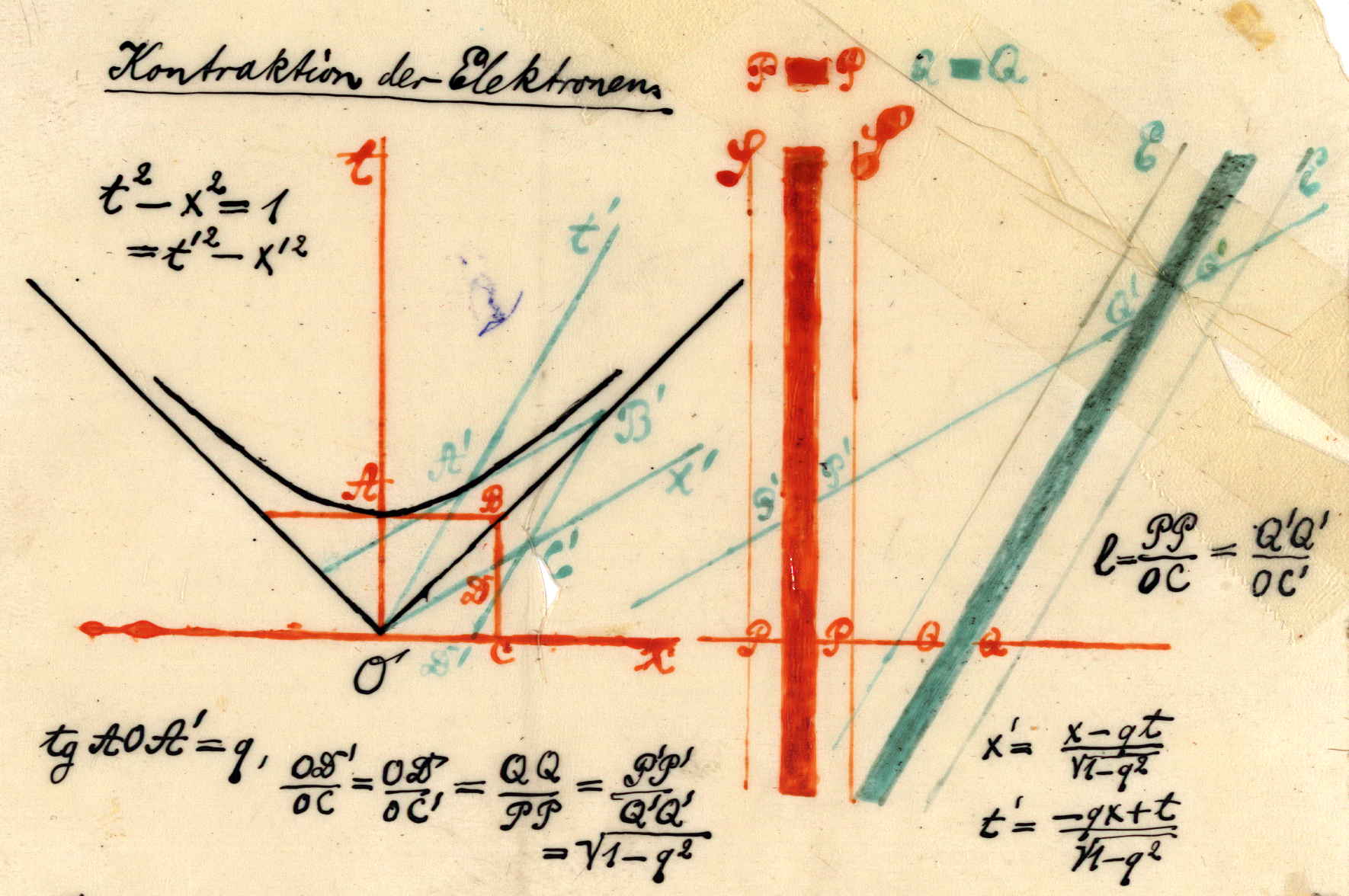
Consequently, in an inertial frame , concrete measuring rods of length contract in their direction of motion with respect to the ether frame according to Lorentz’s formula: , where , and designates the length of the rod in a frame at rest , is the velocity of with respect to , and is the velocity of light, a universal constant. Observers in can correct for the motion-induced Lorentz-contraction of their measuring rods; Poincaré put the correction factor at .2626endnote: 26 See Poincaré (1901, 536), where the value is off by a factor of ten. In a later essay, Poincaré (1904, 312) supplied the “correct” value of the correction factor for terrestrial observers and an ether at rest with respect to the Sun, where .
In his Sorbonne lectures of 1906–1907 (mentioned above), Poincaré employed the light ellipse in pursuit of two objectives. First, he wanted to show that length and time measurements are transitive for inertial observers, transitivity being a sign of objectivity. To do so, he imagined a light source in uniform motion of velocity , that passes through the coordinate origin at time . At a later time , the source reaches a point , such that the light-wave originating at time and propagating in all directions with speed has a spherical wavefront of radius . Fig. 3, redrawn after Vergne’s notes of Poincaré’s lectures, shows a section of the surfaces of two light spheres associated with three successive positions of the source: , , and . The largest light sphere has center , and the smallest has center , as judged by an observer at rest with respect to frame with coordinate origin .
According to Vergne’s notes (2, 49), Poincaré described the “measured length” of the light ellipse to be elongated in the direction of motion. I take this remark to mean that measuring rods are Lorentz-contracted, such that for the resting observer, measured lengths are greater than “true” lengths by a Lorentz factor. Poincaré’s published accounts of the light ellipse do not repeat this particular description of its measured dimensions. Nonetheless, Vergne’s notes illustrate in detail Poincaré’s measurement protocol.2727endnote: 27 The published version of the notes differs markedly from the original, suggesting that their editor, the astronomer Marguerite Chopinet, disagreed with their content; cf. Chopinet (1953, 219).
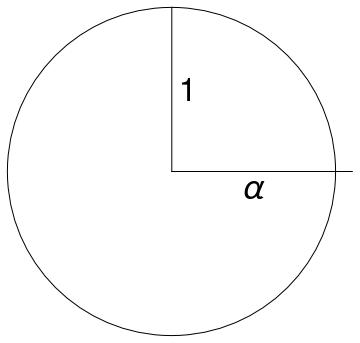
Referring to a unit circle with two segments extending from the center, as in Fig. 4, Vergne’s notes explain the measurement procedure for an observer equipped with a ruler in motion:2828endnote: 28 “Alors je prends une surface rigoureusement spherique. Je la mesure avec mon mètre: dans la direction du mouvement mon mètre sera contracté de ; sa longueur vraie sera devenue . Donc mon diamètre dans le sens du mouvement aura pour longueur mesurée . Dans le sens perpendiculaire la longueur mesurée sera 1. Donc une sphère paraîtra un ellipsoïde allongé dans le sens du mouvement.”
So I take a rigorously-spherical surface, and I measure it with my ruler. My ruler will be contracted by along the direction of motion; its true length will have become . Therefore, along the bearing of motion my diameter will have the measured length . Along the perpendicular bearing the measured length will be 1. Therefore a sphere will appear [as] an ellipsoid elongated along the bearing of motion. (Vergne notebook 2, 49–50, original emphasis)
Fig. 4 shows a horizontal line segment labelled “” extending from the circle center just past the circumference, and a vertical segment labelled “1”, extending from the center of the circle to the circumference.
The dimensions of length measured by a comoving observer are in error due to Lorentz contraction of rulers in motion, leading Poincaré to “correct” for the contraction. Upon correction for the Lorentz-contraction of rulers, Poincaré finds the “true” shape of “rigorously-spherical surface” to be that of an ellipsoid of revolution, the major axis of which is aligned with the direction of motion of the observer and ruler with respect to the ether.
This measurement scheme is novel, but Poincaré went on to identify his “elongated ellipsoid” with the wavefronts of a light pulse, or what we call, for convenience, a light ellipsoid. The exact dimensions of the light ellipsoid depend on the time at which the measurement of the light locus is performed. However, the form of the light ellipsoid is the same for comoving observers, in that the eccentricity is a constant that depends on frame velocity alone, (cf. Poincaré 1908a, 393). Poincaré remarked that in a direction orthogonal to the observer’s motion, there is no motion-induced length deformation, such that the length of the semiminor axis is , where denotes “true” time, i.e., the coordinate time of the ether frame . This remark led Poincaré to argue that apparent temporal duration is transitive for inertial frames, and ultimately, to a derivation of the Lorentz transformation.
The derivation of the light ellipse that Poincaré performed for his students proceeded as follows, based on the ellipse dimensions shown in Fig. 2. From the diagram, Poincaré read off the standard relation for an ellipse with focus :
| (4) |
and then solved for :
| (5) |
The latter equation shows the apparent time to be a linear function of apparent displacement , as desired.2929endnote: 29 Using the relations specified in Fig. 2, we have Rearranging the latter expression in terms of , we find , and substituting the value of from (4) we obtain Poincaré’s expression (5) for apparent time . Although Poincaré did not point this out, by simply rearranging (5), we obtain the transformation
| (6) |
and upon substitution for , we get in terms of :
| (7) |
What Poincaré did point out explicitly to his students (Vergne notebook 2, 51) was just this: since the difference between apparent and true time is a linear function of apparent displacement, the variable that appears in the Lorentz transformation is the apparent time featured in the light ellipse.
In summary, Poincaré associated during his lectures of 1906–1907 a light sphere in of radius with a light-ellipsoid in of semiminor axis of length , and semimajor axis of length , from the dimensions of which he derived the Lorentz transformation. Although he did not realize it, Poincaré’s interpretation of the light ellipse was physically flawed, in that it ascribed to observers physical events that have no causal connection to them. The flaw can be grasped most easily by referring to a cognitive tool that was not available to Poincaré until 1908: the three-dimensional Minkowski spacetime diagram (Walter, 2014).
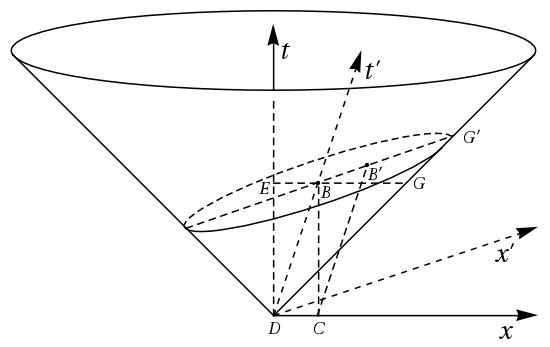
According to the interpretation of the Lorentz group offered in Vergne’s notes, the radius vector of the light ellipse corresponds to light points at an instant of ether time . On a Minkowski diagram, the situation is described by an ellipse lying on a spacelike plane of constant time (Figure 5, with the -axis suppressed for clarity). The ellipse center coincides with spacetime point , and the points , , , and lie on the major axis, such that is a semiminor axis of length . The light ellipse intersects the lightcone in two points, corresponding to the endpoints of the minor axis, and .
In the foregoing Minkowskian representation of the light ellipse, it is plain to see that there are points on the light ellipse that lie outside the lightcone. The latter points represent locations in spacetime physically inaccessible to all inertial observers sharing a spacetime origin. In four-dimensional Minkowski spacetime, the intersection of the light sphere with center and the light ellipsoid with center , where and lie on a spacelike plane, is a circle of radius . On a three-dimensional Minkowski spacetime diagram, where one spatial dimension is suppressed, the corresponding circle with center and ellipse with center intersect in two points, labeled and , such that . The upshot is that Poincaré’s light-ellipse model of the Lorentz group admits superluminal signals. This is certainly not what Poincaré wanted, and it may be assumed that he was not aware of the flaw in his model.
Poincaré published a popular presentation of the light ellipse in an article entitled “The dynamics of the electron”, that appeared on 30 May, 1908. This article recapitulates the presentation of the light ellipse found in Vergne’s notebook, and introduces a discussion of relative velocity, in which Poincaré affirms that we “must evaluate it in local time” (Poincaré, 1908a, 397). While he did not explain how such an evaluation would be performed, the problem of time measurement in inertial frames was clearly posed by Poincaré. Other theorists, including Einstein and Minkowski, had posed the same question, but unlike Poincaré, they admitted that clocks in common uniform motion, synchronized by crossed light signals, are valid timekeepers.
Like Einstein and Minkowski, Poincaré came to admit that clocks in uniform motion are just as valid as clocks at rest in the absolute ether. The occasion for this step was the sixth and final lecture delivered by Poincaré in Göttingen at the invitation of the Wolfskehl Foundation, on 28 April, 1909. Entitled “La mécanique nouvelle”, the lecture was the only one presented in French, as if to underline the Gallic origins of relativity theory for an audience more familiar with the theories of Einstein and Minkowski.3030endnote: 30 The context of Poincaré’s invitation to Göttingen is discussed in Walter (2018).
For his Göttingen audience, Poincaré imagined an observer in motion equipped with light-synchronized clocks and a radio transmitter-receiver.3131endnote: 31 On Poincaré’s engagement with electrotechnology, and wireless telegraphy in particular, see Galison (2003), Gray (2013), and Walter (2017). By exchanging telemetry data with a second observer in relative motion likewise equipped, the first observer comes to the conclusion that his watch is running fast. This situation corresponds to the one invoked by Poincaré in 1908, as mentioned above.3232endnote: 32 One may wonder why the watch in Poincaré’s thought experiment runs fast, and not slow, as would be required by time dilation in an Einsteinian or Minkowskian context. An explanation is at hand, if we focus on the first observer’s experience. At first, he believes he has a certain velocity, say 200km/s. An exchange of telemetry data with the second observer convinces him that he is moving slower than he thought previously. One way for him to account for this revision is to admit that his watch is running fast. Other explanations for the fast watch can be imagined; see Walter (2014).
By allowing clocks to read local time, Poincaré was able to repair the flaw in his interpretation of the light ellipse. A few months after his lectures in Göttingen, he delivered a plenary lecture at the annual meeting of the French Association of Arts and Sciences, in Lille, on the third of August, 1909. In the course of the lecture, he recalled the thought experiment from his talk in Göttingen, and noted this time that, for the two observers and in relative motion,3333endnote: 33 “…un théorème de géométrie très simple montre que le temps apparent que la lumière mettra à aller de en , c’est-à-dire la différence entre le temps local en au moment du départ de , et le temps local en au moment de l’arrivée en , que ce temps apparent, dis-je, est le même que si la translation n’existait pas, ce qui est bien conforme au principe de relativité.”
…a very elementary geometrical theorem shows that the apparent time required for light to travel from to , i.e., the difference between the local time at when the wave leaves and the local time at when the wave reaches , this apparent time, I say, is the same as if the translational motion did not exist, just as required by the principle of relativity. (Poincaré, 1909, 173–174, original emphasis)
The “elementary geometrical theorem” referred to by Poincaré is just (4). By employing apparent time instead of ether time, Poincaré transformed in one fell swoop his light ellipse from a flawed interpretation of the Lorentz group to a model of time dilation and Lorentz contraction.
Poincaré’s employment of apparent time instead of ether time , first communicated during his lecture in Lille, alters the representation of the light ellipse in a 3D-Minkowski diagram (Fig. 6), such that the ellipse lies in a spatial plane of constant . The intersection of a constant-time plane with the lightcone (where ), is a circle of center and radius in frame , while the intersection of the lightcone with a constant-time hyperplane in passing through spacetime point forms an ellipse on a spacetime diagram, corresponding to a circle of center with respect to . Poincaré’s light ellipse (Fig. 2) is identical to the intersection of the lightcone with a spacelike plane in passing through spacetime point on the -axis. The flaw of his previous interpretation of the light ellipse (in Fig. 5), i.e., the existence of hyperlight signals, is no longer present in the Lille interpretation, since all points of the light ellipse lie on the lightcone.

The light ellipse was not a matter of discussion for theorists during Poincaré’s lifetime, and it was rarely discussed after 1912, even though Lorentz adopted the notion of a light ellipsoid in The Theory of Electrons (Lorentz, 1909, 224). The neglect of Poincaré’s light ellipse may be attributed in part to its obscure presentation in the Revue générale des sciences pures et appliqués (1908a), which was the only detailed presentation of the light ellipse to appear until 1913.3434endnote: 34 An excerpt of the Revue article was included in Poincaré’s Science et méthode (Poincaré, 1908b), neglecting mathematical details, such as Poincaré’s discussion of relative velocity. Beyond this particular case, both in France as elsewhere in Western Europe, alternatives to the Einstein-Minkowski theory were often debated, while Poincaré’s theory was considered by almost no one but Poincaré.3535endnote: 35 For a sketch of the French reception of relativity, see Walter (2011).
Among electron theorists, Lorentz followed Poincaré’s work more closely than others, and he applauded Poincaré’s contributions, some of which he adopted, including Poincaré stress (Lorentz 1909, 213). If Lorentz was aware of Poincaré’s light ellipse, he left no trace of it, while he reproduced Einstein’s light-sphere derivation of the Lorentz transformations in the second edition of his Theory of Electrons (Lorentz 1916, 322). Lorentz did not identify the source of the derivation, which suggests that by 1916, it had lost all novelty.3636endnote: 36 Despite Lorentz’s embrace of the what Louis du Pasquier called the “principle of lightwave sphericity”, the Swiss mathematician later wrote that Lorentz rejected this principle (Du Pasquier 1922, 68).
Later investigators, beginning with one of Einstein’s early collaborators, Édouard Guillaume (1922), invoked Poincaré’s light ellipse in a quest to save the notion of absolute time. Guillaume’s view informed the philosopher Henri Bergson’s interpretation of special relativity in terms of “figures de lumière” (Bergson, 1922, 133). These contributions and others are neglected here as they fall outside our temporal scope.3737endnote: 37 On Guillaume’s collaboration with Einstein, see Einstein’s letter to Jacob Laub, 20 March, 1909, in Klein (1993, Doc. 143).
If Poincaré’s geometric point of view is adopted, his light ellipse shows how to construe the Lorentz transformation as a rotation coupled to a dilation.3838endnote: 38 A displacement from one point to another on the light ellipse corresponds to a Lorentz transformation in this interpretation. The radii from a focus to any two points of the ellipse are related by a rotation and, in general, a dilation or a contraction. Given Poincaré’s skill in conceiving intuitive models of curved space,3939endnote: 39 On Poincaré’s models of hyperbolic geometry, see Gray (1989) and Zahar (1997). and in light of the fact that he interpreted the Lorentz transformation algebraically as a pure rotation in four-dimensional space, one wonders if he considered illustrating the Lorentz transformation as a pure rotation. The latter question arises in this historical context, since Minkowski produced such an illustration just a year or so after Poincaré introduced the light ellipse. Minkowski’s theory of spacetime and its relation to the light sphere and the light ellipse are taken up in the next section.
6 Minkowski’s lightcone
Hermann Minkowski was the first mathematician in Germany to take an interest in relativity theory. His fellow mathematicians had long abandoned research in theoretical physics, which in Germany had become the affair of specialists like Max Planck and Ludwig Boltzmann, at least since the founding of physical institutes in the 1870s (Jungnickel and McCormmach, 1986a, b). But like many in mathematics, Minkowski kept abreast of research in analytical mechanics, a subject on which he lectured at Zürich Polytechnic (now the ETH), where Walter Ritz, Albert Einstein, and Marcel Grossmann were among his students. From 1902, he taught this subject and others at the Georgia Augusta University of Göttingen.4040endnote: 40 For background, see Walter (1999a; 2008).
In Göttingen, Minkowski rejoined his friend David Hilbert, and immersed himself in the activities of the local research community. The first decade of the twentieth century was a golden one for science in Göttingen, thanks in part to Felix Klein’s success in attracting investments in new scientific and technical institutes from local industry and government sources, and to the drawing power of the faculty. Students from Europe, Russia, the United States and Japan came to Göttingen to hear lectures by Hilbert, Minkowski, Klein, Walther Nernst, Eduard Riecke, Woldemar Voigt, Karl Schwarzschild, Emil Wiechert, Ludwig Prandtl, and Carl Runge.4141endnote: 41 On the rise of Göttingen as a scientific center, see Manegold (1970) and Rowe (1989).
Electron theory served as a focus of many theoretical and experimental investigations undertaken by Minkowski’s colleagues, although Voigt, Göttingen’s chair of theoretical physics, had assumed a more critical stance. And while neither Hilbert nor Minkowski had published on questions of physics, they were keenly interested in exploring the mathematical side of electron theory, and in the summer semester of 1905, they co-directed a seminar on the subject, attended by Wiechert, the mathematician Gustav Herglotz, Born, Laue and others (Pyenson 1979). Electron-theoretical papers by Lorentz and Poincaré figured prominently on the seminar syllabus, but their most recent publications, in which the principle of relativity and the Lorentz transformation were exploited more fully, were neglected. As for Einstein’s relativity paper, it had yet to be published.
Following the electron-theory seminar, Minkowski delved into another topic of great interest to theoretical physicists: the theory of heat radiation. He lectured on recent work in this area by Planck and Nernst for the Göttingen Mathematical Society in 1906, and offered a course on the subject in the summer semester of 1907. Minkowski’s course notes indicate that he was familiar with Planck’s pioneering article on relativistic thermodynamics (Planck 1907), in which he praised Einstein’s relativity paper. Shortly thereafter, Minkowski wrote to Einstein to request an offprint of this paper, for use in his seminar.
Einstein’s achievement came to Minkowski as a “huge surprise”, according to Max Born, because Minkowski did not believe Einstein possessed the mathematical background necessary to create such a theory (Seelig 1960, 45; Born 1959, 502). From the vantage point of its mathematical expression, Einstein’s electrodynamics of moving bodies is all the more remarkable for its extreme simplicity. A lack of training in advanced mathematics did not constitute a serious handicap for Einstein in theoretical physics, as Hilbert and others pointed out later.4242endnote: 42 See Frank (1947, 206). Miller (1976, 918) emphasizes the relative simplicity of the mathematical tools deployed by Einstein in his relativity paper, in comparison to those Poincaré brought to bear on similar problems. Renn (2007b, 69) observes that Einstein’s uncanny aptitude for informal analysis of complex problems served him well in both special and general relativity. In this respect, Einstein’s electrodynamics of moving bodies contrasts sharply with Minkowski’s memoir on the electrodynamics of moving media (1908), the elegant formalism of which Einstein and other physicists chose at first to ignore.
The full exploitation of light-sphere covariance required a mathematical sophistication somewhat beyond Einstein’s reach in 1905. Mathematicians like Poincaré, Cunningham, and Minkowski were all in a position to explore the consequences of light-sphere covariance in their formal investigations of the principle of relativity, and all of them did so. It is far from clear, however, that Minkowski grasped the essentials of Einstein’s kinematics, of which he gave a frankly distorted account in his essay “Space and Time” (Walter 1999a). As mentioned above, Einstein provided no geometrical interpretation of his kinematics or of the Lorentz transformation. In his essay, Minkowski famously illustrated his spacetime theory with geometric diagrams, and in an effort to distinguish his theory from those of Lorentz and Einstein, he interpreted the latter theories geometrically. Geometric reasoning carried a significant part of Minkowski’s message in this work, as well as in Minkowski’s earlier writings on relativity.4343endnote: 43 Minkowski’s visually-intuitive approach to relativity is explored at length by Galison (1979).
In one of his first attempts to provide a geometric view of the Lorentz transformation, Minkowski drew on Poincaré’s observation that the Lorentz transformation corresponds to a pure rotation in four-dimensional space (, , , ). During the course of a posthumously-published lecture for the Göttingen Mathematical Society on 5 Nov. 1907, Minkowski brought up the quadratic expression , which he expressed in the Euclidean form , via the substitution of , , , , for the coordinates , , , i (Minkowski, 1915, 374). With this substitution, a re-expression of the laws of physics in four-dimensional terms was at hand, the premises of which Minkowski laid out in his lecture. First, however, he explored the geometry of his four-dimensional space, noting an application of hyperbolic geometry.4444endnote: 44 On Minkowski’s use of hyperbolic geometry in this lecture, see Reynolds (1993). He described the hypersurface
| (8) |
as a calibration curve of sorts, in that any line from the origin to a point on this hypersurface may be identified with the temporal axis of an inertial frame of reference. The hypersurface of equation (8) may also be expressed, Minkowski observed, in the form of a pseudo-hypersphere of unit imaginary radius
| (9) |
Both hypersurfaces (8) and (9) were known to provide a basis for models of non-Euclidean geometry.
The hypersurface (8) thus corresponds to the set of four-velocity vectors. Although Minkowski did not spell out the interpretation, he probably recognized that a displacement along (8) corresponds to a rotation about the origin, such that frame velocity is described by a hyperbolic function, . However, he probably did not yet realize that his hypersurfaces represent the set of events occurring at coordinate time of inertial observers, the worldlines of which pass through the origin. According to (8), this time is imaginary, which may have obscured the latter interpretation. In fact, Minkowski did not yet possess the notion of a worldline, or of proper time (Walter, 2007a, 217).
Sometime before the end of 1907, Minkowski discovered both worldlines and proper time, along with the lightcone structure of spacetime; he published these insights in an appendix to his theory of the electrodynamics of moving media, on 5 April 1908. The Lorentz transformation, he realized, could be written in trigonometric form, by invoking circular functions with an imaginary argument i:
where , and . Frame velocity is then expressed in terms of a tangent, . In this imaginary-angle form, the two-dimensional Lorentz transformation may be interpreted as a pure rotation about the center of a circle of imaginary unit radius. Minkowski’s followers showed that in the real form, the Lorentz transformation may be construed as a displacement along a unit hyperbola. This unit hyperbola and the circle of imaginary unit radius correspond to the surfaces (8) and (9), with two spatial dimensions suppressed.
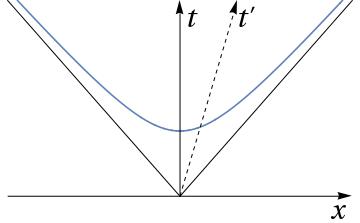
In Minkowski spacetime, Einstein’s light-sphere covariance gives way to lightcone covariance. Minkowski interpreted Einstein’s expression (1) for a light sphere as the equation of a lightcone in spacetime. Whereas both Einstein and Poincaré understood light-waves in empty space to be the only physical objects immune to Lorentz contraction, Minkowski saw that when light-rays are considered as worldlines, they divide spacetime into three regions, corresponding to the spacetime region inside a future-directed () hypercone (“Nachkegel”), the region inside a past-directed () hypercone (“Vorkegel”), and the region outside any such hypercone pair. The propagation in space and time of a spherical light-wave is described by a hypercone, or what Minkowski called a lightcone (“Lichtkegel”).
One immediate consequence for Minkowski of the lightcone structure of spacetime concerned the relativity of simultaneity. In a section of his paper on the electrodynamics of moving media entitled “The concept of time”, Minkowski (1908, § 6) showed that Einstein’s relativity of simultaneity is not absolute. While the relativity of simultaneity is indeed valid for two or three simultaneous “events” (Ereignisse), the simultaneity of four events is absolute, so long as the four spacetime points do not lie on the same spatial plane.4545endnote: 45 “Werden jedoch vier Raumpunkte, die nicht in einer Ebene liegen, zu einer und derselben Zeit aufgefaßt, so ist es nicht mehr möglich, durch eine Lorentz-Transformation eine Abänderung des Zeitparameters vorzunehmen, ohne daß der Charakter der Gleichzeitigkeit dieser vier Raum-Zeitpunkt verloren” (Minkowski 1908, 69). Minkowski’s demonstration relied on the Einstein simultaneity convention, and employed both light signals and spacetime geometry, but not the light sphere. His result showed the advantage of employing his spacetime geometry in physics, and later writers, including Poincaré, appear to have agreed with him, by considering the discovery of the existence of a class of events for a given observer that can be the cause of no other events for the same observer as a consequence of spacetime geometry (Walter 2009, 210).
Physicists in Germany quickly seized upon Minkowski’s electrodynamics of moving media, but as mentioned above, they stripped it of the four-dimensional formalism in which it had been dressed by its inventor. In what became the standard response to Minkowski’s electrodynamics of moving media, both in Germany and abroad, Minkowski’s former students Einstein and Jacob Laub recast Minkowski’s four-dimensional expressions in terms of ordinary vectors. In 1908, outside of Göttingen and Cambridge, theorists saw no use at all for a four-dimensional approach to physics.
One imagines that for Minkowski, this was a vexatious state of affairs. According to his former student Max Born, Minkowski always aspired
to find the form for the presentation of his thoughts that corresponded best to the subject matter. (Born, 1914)
The form Minkowski gave to his theory of moving media had just been judged unwieldy by his readers, and in the circumstances, decisive action was called for if his formalism was to survive at all. In September 1908, he took such action, by affirming the reality of the four-dimensional “world”, and its necessity for physics (Walter 2010). His celebrated lecture “Raum und Zeit”, delivered at the annual meeting of the German Association of Scientists and Physicians in Cologne, offered two diagrammatic readings of the Lorentz transformation, one attributed to Lorentz and Einstein, the other to himself.
The first of these two readings was supposed to represent the kinematics of the theory of relativity of Lorentz and Einstein. In fact, Minkowski’s reading captured Lorentzian kinematics, but distorted Einsteinian kinematics, prompting corrective action from Philipp Frank, Guido Castelnuovo, and Max Born.4646endnote: 46 See Born (1909, 9; 1959, 503). For further references and details on Minkowski’s distortion and its reception, see Walter (1999a). The idea stressed by Minkowski was that in the (Galilean) kinematics employed in Lorentz’s electron theory, time being absolute, the temporal axis on a space-time diagram may be rotated freely about the coordinate origin in the upper half-plane (), as shown in Fig. 8. The spatial position of a point may be described with respect to frames and , corresponding to the coordinate axes and , respectively, according to the coordinate transformation: , .
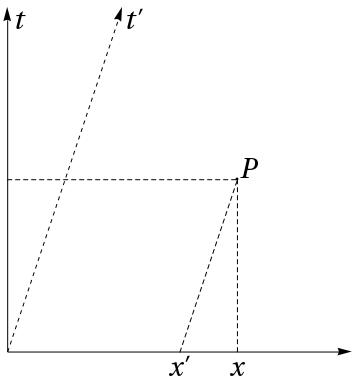
In contradistinction to the latter view, the theory proposed by Minkowski required a certain symmetry between the spatial and temporal axes. This constraint on symmetry itself was sufficient for a geometric derivation of the Lorentz transformation. Although Minkowski described his spacetime diagram as an illustration of the Lorentz transformation, he did not spell out the interpretation in detail. Nonetheless, Minkowski did provide a geometric derivation of the Lorentz transformation at some point, as attested by an autograph slide in Minkowski’s Nachlass, which may have been projected during the lecture he delivered to the German Association of Scientists and Physicians in Cologne.4747endnote: 47 NSUB Handschriftenabteilung. The demonstration missing from the published text of Minkowski’s lecture was later supplied by Arnold Sommerfeld, in an editorial note to his friend’s lecture. The annotated version of the lecture appeared in an anthology of papers on the theory of relativity edited by Otto Blumenthal (1913). According to Rowe (2009, 37), Sommerfeld was the driving force behind the latter anthology.
While Minkowski acknowledged Einstein’s critique of absolute time, he considered that the concept of a rigid body – upon which Einstein had based his relativistic kinematics – made no sense in relativity theory (Minkowski 1909, 80). Similarly, Poincaré deemed that measurement in relativity theory could no longer rely on the displacement of rigid bodies, which were replaced for the purpose of measurement in Lorentz’s theory by light time-of-flight (§ 3). For Poincaré and Minkowski, Einstein’s foundation of relativistic kinematics on the behavior of ideal clocks and rigid rods did not sit well at all with the Lorentz-deformation of displaced solids. They did not appeal to the kinematics of rigid bodies to derive the Lorentz transformation, but affirmed the principle of relativity, and required that the transformations of coordinates between inertial frames form a group.4848endnote: 48 As seen above, Poincaré also derived the Lorentz transformation from the assumption of Lorentz contraction of concrete rods, and the isotropy of light propagation for inertial observers. He later considered (apparent) time deformation as a consequence of the principle of relativity and Lorentz contraction; see (Poincaré 1913, 44). For Minkowski, Lorentz contraction of electrons was a direct consequence of the geometry pertaining to this group.
The latter consequences were displayed by Minkowski on a spacetime diagram, and elaborated upon by Sommerfeld on the occasion of a reedition of Minkowski’s Cologne lecture (Sommerfeld 1913). Minkowski’s spacetime diagram thus offered a novel means of understanding the strange consequences of Einstein’s kinematic assumptions. However, the spacetime diagram was understood by some physicists to lend support to an ether-based outlook, as shown by Emil Wiechert’s contributions (discussed in § 9).
7 Alfred A. Robb: repurposing the lightcone
A physicist trained in Belfast, Cambridge, and Göttingen, Alfred A. Robb (1873–1936), found the means in Minkowski’s spacetime geometry to realize an “optical geometry of motion”, in which he could dispense with Einstein’s ideal clocks and rigid rods (Robb, 1911). Robb, described by Larmor (1938, 320) as an “unremarkable” graduate of St. John’s College, Cambridge, was ranked fifty-second (ex aequo) in the 1897 Mathematical Tripos.4949endnote: 49 Tanner (1917, 571). I thank J. Barrow-Green for pointing me to this source. He went on to write a theoretical study of the Zeeman effect in Göttingen under W. Voigt’s direction, published in the Annalen der Physik (1904), after which he returned to St. John’s, and joined the Cambridge Philosophical Society.5050endnote: 50 Robb was admitted to the Society on 27 Nov. 1905 (Proceedings of the Cambridge Philosophical Society 16, 1912, p. 16).
In his doctoral thesis, Robb took up one of the more puzzling problems facing physicists in the early twentieth century: to explain the patterns of magnetic splitting of atomic spectral lines, known then as the complex Zeeman effect. Starting from Lorentz’s Nobel-prize-winning theory of doublet and triplet lines (1897), Robb introduced elastic forces between electron pairs, triplets, and quadruplets. To obtain agreement with observation, he introduced a geometric constraint, requiring electrons to oscillate on the surface of a cone. As he wrote to Larmor, the “restrictions are so peculiar that one may be inclined to doubt the theory”, and indeed, Robb’s scheme was later described by Lorentz as both “very ingenious” and “so artificial”.5151endnote: 51 Robb to Larmor, 6 March 1904, Larmor Papers, St. John’s College Library; Lorentz (1909, 115). Voigt sent Lorentz a copy of Robb’s dissertation; see Lorentz to Voigt, 18 Dec. 1904, in Kox (2008, § 121).
Much like his theory of the complex Zeeman effect, Robb’s optical geometry was both ingenious, and unattractive to physicists. Yet Robb’s geometry laid the groundwork for a theory of time and space that was later hailed by the likes of Hermann Weyl (1922, 209). To build his optical geometry, Robb borrowed some basic insights from Minkowski, and transformed them as needed. For example, he employed Minkowski’s trigonometric definition of velocity , in a real hyperbolic form, such that , and called the “rapidity” of the particle.5252endnote: 52 In a letter to Larmor of 18 Jan. 1911, the Cambridge mathematician A. E. H. Love wrote that he had “noted explicitly in writing” to Robb that one of his formulas was from Lobachevski geometry, and that “space might be saved by bringing this fact in” (Larmor Papers, St. John’s College Library). On Robb’s use of hyperbolic geometry, see Walter (1999b). Taking a cue from the Minkowski spacetime diagram, Robb described particle velocity with respect to the index-axis via the relation , and expressed the lightcone in terms of orthogonal axes :
| (10) |
where the -axis represents a temporal index, the vertex coincides with the origin, and the speed of light is unity.
For purposes of illustration, Robb followed Minkowski’s convention on units, such that the path of light in vacuum is described for any inertial observer by a line forming an angle of with the -axis. In the place of Einstein’s notion of distant simultaneity, Robb introduced a more restrictive definition, whereby the emission or reception of two or more light signals is simultaneous if and only if it is observed at a single spatial location at a single instant of time by a colocated, inertial observer. Simultaneity is an absolute notion in Robb’s scheme, and the distance to a particle of matter in arbitrary motion is determined by round-trip light time-of-flight between the inertial observer and the particle.
Light-rays play a fundamental role in Robb’s geometry of phenomenal space, as the title of his booklet suggests. Issues of clock synchronization do not arise here, nor is there any question of transforming measured quantities. However, Robb was careful to show that according to his theory, lengths of material bodies “appear to be shortened in the direction of motion”, a result in agreement with other relativity theories.5353endnote: 53 For Robb the “appearance” of contraction was a necessary consequence of light time-of-flight measurements. Robb, Einstein, and their contemporaries focused on the instantaneous form of moving objects, in an approach distinct from the one adopted in the late 1950s. The latter studies characterized what Roger Penrose (1959) referred to as the “photographic” appearance of a moving object. Moreover, to demonstrate this result, Robb implicitly borrowed Poincaré’s idea of using a light shell as a metric surface. Yet Robb openly distanced himself from Poincaré’s conventionalist philosophy of geometry:
Speaking of the different “Geometries” which have been devised, Poincaré has gone so far as to say that : “one Geometry cannot be more true than another; it can only be more convenient.” [..] In reply to this; it must be remembered that the language of Geometry has a certain fairly well defined physical signification which in its essential features must be preserved if we are to avoid confusion.5454endnote: 54 Robb (1911, 1), original emphasis. Cf. Poincaré, Science and Hypothesis (1905a, 50).
From the latter remark, Robb’s philosophical position appears closer to Einstein’s contemporary view of a physical geometry realized by ideal rigid rods and clocks, than to Poincaré’s conventionalist doctrine, which ruled out any empirical determination of the geometry of phenomenal space. But as mentioned above, Robb did not admit Einstein’s distant simultaneity, rigid rods, or ideal clocks.
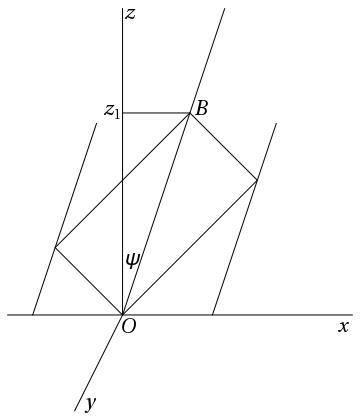
Robb’s philosophy of geometry was an innovative response to the relativity theories of Einstein, Poincaré, and Minkowski, that he developed from around 1910 until the end of his life.5555endnote: 55 For appreciations of Robb’s geometry, see Briginshaw (1979), and Cat (2016). In his first publication on geometry (1911), Robb’s philosophy found expression in an original analysis of the form of a reflected light-shell for an observer in motion. His approach to this problem employed a diagram of a three-dimensional space, redrawn here as Fig. 10; it may be summarized briefly as follows. An observer in uniform motion along the -axis with velocity transmits a number of light signals in the -plane at an instant of time with index . These signals are reflected from a ring of comoving particles surrounding the observer in such a way that the signals arrive at the observer’s location at point at a single instant of time of index . Neglecting one spatial dimension, Robb’s diagram shows a future-lightcone from the origin in -space that intersects with a past-lightcone with vertex at point . The intersection of the two lightcones defines an ellipse on an oblique plane, which is not illustrated in Robb’s diagram, but which contains a diagonal of the rectangle in Fig. 10, and forms an angle with the -axis. By way of comparison, in Minkowski three-dimensional spacetime the latter plane corresponds to a spacelike plane of an observer in motion with velocity .
Iteration of the signalling process produces a representation of an elliptic cylinder of axis , the equation for which Robb derived. From the perspective of an observer at rest with respect to the origin, Robb argued, the “apparent form of this ring of particles” is given by a section of the cylinder in the -plane. In other words, the apparent form, for an observer in the rest frame, of the (reflected) light-shell of an observer in motion is an ellipse of eccentricity , the minor axis of which is aligned with the ring’s direction of motion. Naturally, Robb concluded that the length of objects in motion, when measured by light time-of-flight, appears to a resting observer to be contracted in the direction of motion.
Although Robb did not say as much, his observer in motion is in a position to conclude that the reflecting ring of particles forms a circle. If Robb’s observer assumes, with Poincaré, that her concrete rods are Lorentz-contracted, she may correctly infer that her light shell is an elongated ellipsoid, the dimensions of which agree, moreover, with Poincaré’s light-ellipsoid. Robb’s measurement protocol, however, featured no such concrete rods. Furthermore, unlike Poincaré, Robb admitted no privileged frame of reference. Consequently, Robb could no more uphold Poincaré’s homotheticity of light-ellipsoids than he could affirm Einstein’s covariance of light spheres. His preferred figure of light was the lightcone.
In late 1910, Robb had submitted a like-titled work for publication in the Proceedings of the London Mathematical Society (LMS).5656endnote: 56 LMS Council Minutes, 10 Nov. 1910, LMS archives. One of the Society’s two secretaries (along with J. H. Grace), A. E. H. Love asked Robb to “withdraw his paper temporarily”, in order to address the criticisms of a referee. Robb appears to have complained about Love’s request to his former teacher at St. John’s, and LMS council member, Joseph Larmor. In response to Larmor’s query, Love wrote that a referee had found the geometrical part of Robb’s paper to be “extremely illogical”, and had recommended rejection. Love noted that the theory of relativity also entered into the referee’s assessment: Robb’s time index formula was “suggested by Einstein’s work”, and furthermore, the referee felt “it might be necessary to adopt Einstein’s assumptions in order to have some basis for Robb’s formula.”5757endnote: 57 Love to Larmor, 18 Jan. 1911, op. cit. Sedleian Chair of Natural Philosophy at Oxford since 1899, Love was Secretary (i.e., managing editor) of the LMS from 1890 to 1910. The LMS reviewer’s critical assessment of Robb’s work was echoed in softer terms by the Cambridge logician P. E. B. Jourdain (1879–1919). According to Jourdain’s published abstract, the formulas in Robb’s booklet agreed with those of Einstein, Minkowski, and Sommerfeld, but the concepts he employed, including that of the index of a particle, were such that no summary could be provided.5858endnote: 58 Jahrbuch über die Fortschritte der Mathematik 43, 1911, p. 559. A succinct summary of Robb’s index concept is provided by Barrow-Green and Gray (2006).
From these assessments, it appears that Robb’s theory was seen in England as a confusing, mathematically-inept variant of Einstein’s theory. The decision by the LMS council to follow Grace and Love’s recommendation against publication of Robb’s manuscript meant his theory would not benefit from a stamp of authority from Britain’s leading mathematicians and theoretical physicists.5959endnote: 59 LMS Council Minutes, 9 Feb. 1911, LMS archives. Robb’s rejected manuscript then became a booklet, the preface to which, dated 13 May 1911, suggests that its author was still smarting from the LMS council’s negative decision:
From the standpoint of the pure mathematician Geometry is a branch of formal logic, but there are more aspects of things than one, and the geometrician has but to look at the name of his science to be reminded that it had its origin in a definite physical problem.
That problem in an extended form still retains its interest.
The italics in the passage above are Robb’s, underlining the triad: geometry–logic–physics. Beyond the expected retort to the censorious pure mathematician, Robb’s preface affirmed his identity as a “geometrician”, and his consequent right to “extend” the domain of application of geometry beyond that of both logic and the measurement of length intervals in the phenomenal space of physics.
From the LMS council’s rejection of Robb’s theory of relativity, one gathers that this theory had its detractors. But as mentioned above, the theory had its admirers, as well. One of these admirers was Ludwig Silberstein (1872–1948). A former doctoral student of Max Planck in Berlin, Silberstein wrote The Theory of Relativity (1914), one of the first two textbooks on the subject to be published in England, with Cunningham’s The Principle of Relativity (1914). A lecturer in mathematical physics in Rome since 1903, Silberstein based his textbook on lectures delivered at University College London in 1912–1913. In his preface, Silberstein explained his wish “to trace the connexion of the modern theory with the theories and ideas that preceded it”. The modern theory Silberstein referred to here was essentially that of Einstein and Minkowski.
In a chapter of his textbook entitled “Various Representations of the Lorentz Transformation”, Silberstein recommended Minkowski diagrams, described as “very advantageous, especially for the trained geometer of our days” (Silberstein, 1914, 131). His overview of the “geometric representation” of the Lorentz transformation began with a two-dimensional spacetime diagram, illustrated by a figure showing two pairs of coordinate axes, the conjugate hyperbolas and , and their asymptotes. He recalled that for any real number , the two families of hyperbolas and are Lorentz-covariant. Extending his arguments to three spacetime dimensions, and then four, Silberstein observed (p. 139) that the spacelike hypersurface () intersects the hyperboloid in a unit sphere, . A non-zero rotation of this hypersurface about the origin in a plane orthogonal to the -axis cuts the hyperboloid in an ellipsoid, resulting in a primed space, , and an assorted orthogonal axis, . Silberstein continued:
Take the semi-diameters of this ellipsoid as the new units of length measured from the origin along any direction in the -space. Then the Lorentz transformation, from to , will be completed, and the new metric surface which, from the -point of view, is an ellipsoid of revolution will for the -standpoint become a sphere,
According to Silberstein’s analysis, the intersection of a -constant hypersurface with a Lorentz-covariant hyperboloid in spacetime is an ellipsoid of revolution in the -frame, and a sphere in the -frame.
8 Applications of the light sphere
Minkowski’s spacetime theory was understood to be consistent with Einstein’s concept of light-sphere covariance, the latter being considered both as a special case of Lorentz-covariance of the laws of physics, and as a mathematical theorem. The figure of a light sphere, however, was never discussed by Minkowski. Nonetheless, physicists like Emil Wiechert (1911, 691) understood the derivation of the Lorentz-transformation from form-invariance of the light-sphere equation to be the true “point of departure” of Minkowski’s spacetime theory. Such a reading suggests that Einstein’s light sphere prepared scientists for the formal requirement of Lorentz-covariance for the laws of physics, as manifested in Minkowski’s theory, and as realized in four-dimensional vector and tensor algebras by Sommerfeld, Abraham, Gilbert Newton Lewis, Laue, and others.
Minkowski employed the equation of a light sphere in his representation of the Lorentz transformation by postulating the invariance of the quadratic form:
| (11) |
where the velocity of light is rationalized to unity (Minkowski 1908, 66). Next, invoking the substitution for coordinates , , , i, Minkowski expressed the general Lorentz transformation in terms of a coefficient matrix ,
| (12) |
with determinant unity such that
| (13) |
Cunningham was struck by Minkowski’s equation (12), and by the fact that Minkowski’s restriction on the determinant could be relaxed, while preserving the form of the wave equation.6060endnote: 60 Cunningham (1914, 87–89); for an analysis of the procedure, see Newman & Price (2010). The latter insight was exploited in the papers he and Bateman published on the conformal transformations of Minkowski spacetime in 1909–1910. In addition to the form (12), Cunningham acknowledged Minkowski’s interpretation of the Lorentz transformation in relation to the light-wave equation:
It has been pointed out by Minkowski that in a space of four dimensions in which the coordinates are (, , , ), the geometrical transformations employed by Einstein, is simply a finite rotational displacement of the whole space about , . The equation […] is known to be invariant for such a transformation. But this equation is invariant for a larger group of transformations than that of rotations, viz., for the group of conformal transformations in the four dimensional space, which, as is known, is built up out of inversions with respect to the hyperspheres of the space. (Cunningham, 1910, 79)
Cunningham noted further (p. 80) that the hyperspace (, , , i) is conformal to the hyperspace (, , , i) in virtue of the form-invariance of the light-sphere equation. He was, however, not the first to notice the conformal covariance of the wave equation in Minkowski spacetime. For the latter insight, Cunningham acknowledged a remark made to him by his former colleague in Liverpool, Harry Bateman.6161endnote: 61 See Cunningham (1910, 79). As for Bateman, he credited Cunningham with the discovery of the conformal transformations of the equations of electrodynamics; see Bateman (1910c, 224).
Following his success in the Mathematical Tripos, Bateman undertook two years of postgraduate study in Paris and Göttingen, then major centers for experimental and theoretical research on electrons. A central topic of discussion in mathematical physics at the time, the electron theories of Lorentz and Larmor were introduced to French readers by Poincaré and Liénard starting in 1897 (Buchwald 1985). Similarly, in Göttingen, Emil Wiechert, Karl Schwarzschild, and Max Abraham contributed to electron theory, while the mathematicians Hilbert and Minkowski co-led seminars on electron theory and electrodynamics in 1905 and 1907, respectively (Pyenson 1979). When Bateman studied in Göttingen, he was particularly impressed by Hilbert’s approach to integral equations, a subject he taught at Cambridge in 1908.6262endnote: 62 L’Enseignement mathématique 10 (1908), 336; Bateman to Hilbert, 1909, Nachlass Hilbert 13, Handschriftenabteilung, NSUB Göttingen.
Returning to England in 1906, Bateman joined Cunningham as a lecturer at the University of Liverpool. There he applied W. Thomson’s method of inversion to geometrical optics, and found the form of the differential equation for light-wave propagation to be preserved under conformal transformations of four-dimensional (Minkowski) space, much as Minkowski had observed with respect to the transformations of the (inhomogeneous) Lorentz group.6363endnote: 63 See Minkowski (1909), where the Lorentz transformation is attributed to a paper published in 1887 by Voigt. Minkowski described the covariance of the differential equation of light-wave propagation as the “impetus and true motivation” for assuming the covariance of all laws of physics with respect to the transformations of the Lorentz group (p. 80). Bateman also remarked that his method gave rise to a “geometrical construction” in ray optics, whereby a sphere of radius and center corresponds to an inverse sphere of radius with center . In other words, light spheres transform into inverse light spheres.6464endnote: 64 See Bateman (1908, 629), read 8 Sept. 1908. No mention is made in this paper of the source of the transformations, but a subsequent work by Bateman credits Cunningham with the “discovery of the formulæ of transformation in the case of an inversion in the four-dimensional space,” and cites papers by Hargreaves and Minkowski employing a four-dimensional space with one imaginary axis (Bateman 1909, 224, communicated 9 Oct. 1908). Minkowski’s paper (1908, published 5 April 1908) was cited by both Cunningham and Bateman. Remarked first by Whittaker (1953, 195), the significance of Minkowski’s spacetime theory for the contributions of Cunningham and Bateman is contested by Warwick (2003, 423 n. 49). On the “light-geometric approach” to the foundations of relativity by Cunningham and Bateman, see Jammer (1979, 222).
Cunningham and Bateman were atypical in their rapid assimilation of Minkowski’s four-dimensional approach to electrodynamics, a fact which may be attributed in part to local factors, including their training in mathematics. In particular, the technique of conformal transformation was part of the Wrangler’s mathematical arsenal from at least the mid-1890s, and studies of the conformal group in space of dimensions () were familiar in Cambridge at the turn of the century.6565endnote: 65 For example, see Warwick (2003, 421) and Bromwich (1901). In Bateman’s case, postgraduate studies in Göttingen in 1906 afforded him personal acquaintance with Hilbert and Minkowski, both of whom were instrumental in the elaboration and diffusion of four-dimensional approaches to physics. In a fashion similar to that of the latter pair, but on a smaller scale, Cunningham and Bateman employed and promoted four-dimensional techniques: Bateman (1909) published Maxwell’s equations and Lorentz’s microscopic equations in four-vector form, while Cunningham’s treatise on relativity (1914) featured an introduction to four-dimensional vector calculus.
Some of the earliest contributions to relativity theory are due to one of the youngest relativists: Max Laue (1879–1960). A former doctoral student, then assistant to Max Planck, upon whose suggestion he wrote a doctoral dissertation (Laue 1903) on interference phenomena, Laue first heard of Einstein’s relativity paper in Planck’s colloquium. As he recalled later, he found that Einstein’s paper presented “epistemological difficulties” that he was initially unable to master.6666endnote: 66 Laue (1961, XVIII–XXI); Laue to Margot Einstein, 23 Oct. 1959, cited by Holton (1965, 39).
Over the next five years, Laue came to master a few of the difficulties presented by Einstein’s theory, beginning with the derivation of the Fresnel drag coefficient from the velocity addition formula (1907). He adopted a comparative approach to the electrodynamics of moving bodies, publishing a series of papers evaluating the various theoretical options. One of his first contributions compared the electron theories of Abraham and Lorentz to what he called Einstein’s “theory of relativity” (Laue 1908, 838). The differences between the two electron theories, Laue found, were too small to matter as far as the radiation from a charged particle in motion was concerned, but there was an advantage in adopting Einstein’s theory, in that it was “much simpler” to solve the latter problem (ibid.). When in 1911 Laue extended Minkowski’s four-dimensional approach to the dynamics of matter via the formal concept of a “world-tensor”, he was able to shed new light on the nature of Poincaré’s hypothetical binding potential, later known as “Poincaré pressure”, and on the null result of the Trouton-Noble experiment of 1903.6767endnote: 67 Laue (1911b); Janssen & Mecklenburg (2006).
Recognizing Laue’s skill in addressing the questions posed by relativity theory, the publishing house of Vieweg asked him in 1910 to write what was to become the first textbook on relativity.6868endnote: 68 Laue (1952). There Laue identified Einstein as the principal founder of the theory of relativity. He did so, however, while expounding a four-dimensional vector calculus he attributed to Minkowski, but which owed more to Sommerfeld’s formalism.6969endnote: 69 See Max Born’s review in Physikalische Zeitschrift (1912). Laue’s text thus helped established Einstein as a leading theorist in the new field of relativity, and to promulgate four-dimensional tensor calculus.7070endnote: 70 On Laue’s portrayal of Einstein’s contribution, see Staley (1998). Laue’s contributions to relativity are detailed by Norton (1992) and Rowe (2008).
One of the results Laue included in his textbook was the light-sphere-based illustration of the relativity of simultaneity. Laue’s argument and illustration drew on an idea expressed earlier by Planck in lectures delivered at Columbia University in 1909, and published the following year. Planck wanted to convey graphically what he called the “new difficulty” introduced by the principle of relativity, concerning the propagation velocity of light in the ether (Planck, 1910, 113). To do so, he referred to two diagrams (see Fig. 11), representing a section of a light sphere for observers and , respectively, with relative velocity . Taken separately, each of the two diagrams suggests that light isotropy is valid only for observers at rest, since apparently, only such observers will find themselves at the center of the light sphere. Planck stressed, however, that no known physical phenomena distinguished the two frames, and that the difficulty could be overcome by admitting, with Einstein, the Lorentz-covariance of the laws of physics (Planck, 1910, 121).7171endnote: 71 Planck’s argument, which builds on that of Einstein (see above, § 2), has inspired many textbook authors. For an example employing a spherical array of photomultipliers at rest in two inertial frames in relative motion, see Rosser (1967, 76).
Laue took a different approach, by adapting Planck’s light figures, in order to address the notion of relative simultaneity. Repeated in six editions by 1956, Laue’s light figure became a staple of presentations of relativity theory. Pared to essentials, his argument (Laue, 1911a, 34) focused on the simultaneity relation as judged by two observers, respectively at rest, and in uniform motion. A “short light-signal” is emitted in all directions by a source at rest at a “material point” in inertial frame at time . If the origin of coordinates is fixed at point , then at time , the light signal reaches the points described by the equation:
| (14) |
Let two “material points” and at rest in be equidistant from the point , such that the light signal reaches them both at time in . Let a second frame translate uniformly with respect to , in a direction parallel to the line segment joining and , such that the material points , , have velocity with respect to . In , furthermore, the origin of the primed coordinates , , , coincides with that of at time . A light signal propagating in all directions from point at time will reach the surface of a certain sphere at time , such that:
| (15) |
The center of the light sphere in at time coincides with point , as shown in Fig. 12, while the origin of has travelled a distance from , and is located at point with respect to frame .7272endnote: 72 Laue’s use of primes in his light-sphere diagram is peculiar, but is reproduced intact in Fig. 12, in keeping with the first four editions of his textbook (up to 1921). In the sixth edition (1955, 29), , , and are all unprimed, and the primed symbols are as expected: and . With these preliminaries in place, Laue concluded that in frame there exists no value of time for which the material points and lie on the same spherical surface, and that consequently, and are not reached by the light signal simultaneously in frame .


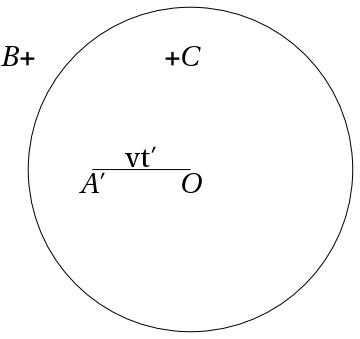
What the diagram shows, Laue wrote, is that in frame , a light signal reaches point before it reaches point . For every inertial system, he concluded, there is a “particular time, differing from that of other systems”. For this insight, Laue credited the “acuity and elevated philosophical sense of Einsteinian ideas”, and proceeded to derive the Lorentz transformation, invoking the form-invariance of the wave equation, along with linearity and symmetry constraints, and noting the fact that the Lorentz transformation follows just as well from the invariance of the sum of squares
| (16) |
The light sphere formed the centerpiece of Laue’s discussion of the Lorentz transformation. As mentioned above, Cunningham and Einstein had employed the light-sphere demonstration in 1907. The fact that Laue preferred to invoke the form-invariance of the wave equation in his textbook is of no particular significance, as he, too, went on to employ the light-sphere demonstration (see Laue 1913b, 110).
Laue’s treatise skillfully combined and repackaged results obtained in the new field of relativity, including the Minkowski diagram and the light-sphere interpretation of the Lorentz transformation and simultaneity relations. The treatise featured the light sphere in a discussion of the foundations of relativistic kinematics and, in the revised and extended second edition of 1913, employed the term “light sphere” in this context (Lichtkugel, 1913a, 36).
Both the relativity of simultaneity and the proof of the Lorentz transformation had previously been demonstrated with a light sphere by Otto Berg (1874–1939), a Privatdozent at the University of Greifswald, in an essay entitled “The relativity principle of electrodynamics”. Taking his cue from Minkowski’s bold claim that the new ideas about time and space in relativity theory had sprung from the ground of experimental physics (Minkowski, 1909), Berg, an experimental physicist, prefaced his pamphlet with the opinion that “many philosophers will doubt” such a claim. He then set out to examine the “experimental foundations of the principle [of relativity]”, a topic Minkowski had scrupulously avoided. In light of Bucherer’s attack on the utility of the light-sphere hypothesis for explaining experimental results, mentioned above (§ 2), Berg’s recourse to the light sphere in this essay comes as a surprise. But as Berg observed, the “clarification of ideas” in relativity theory realized by Einstein and Minkowski had “hardly anything” to do with experiments. In any case, Lorentz’s theory was “just as good” as the newer theories, as far as representing the latest experimental results was concerned (Berg, 1910, 357).
Berg’s treatment of the relativity of simultaneity differed little from that of Laue, mentioned above, with one exception: Berg did not illustrate his discussion with a diagram. He presented his light-sphere demonstration of the relativity of simultaneity as a “concrete example” of Einstein’s light-postulate, and one that later served his derivation of the Lorentz transformation. Laue must have admired Berg’s approach, as he employed it without change, apart from the addition of a graphic illustration (redrawn here as Fig. 12).
Laue’s light-sphere-based demonstration of the relativity of simultaneity had another forerunner in the person of Harry Bateman. Following Cunningham’s lead, Bateman (1912, 340) reckoned Einstein’s light postulate to be equivalent to admitting the existence of a group of transformations for which (16) is covariant. By mid-1910, Bateman (1910b, 624) realized that the Lorentz transformation did not alter the form of tangent oriented spheres. This insight may be what led him to attribute the origin of the Lorentz transformation not to Voigt, in the manner of Minkowski (1909), but to the French differential geometer Albert Ribaucour, known for his contributions to the geometry of spheres (Ribaucour 1870).
In virtue of his understanding of the relation between the Lorentz transformation and the fifteen-parameter group , Bateman went on, in a paper completed in December 1910, to compare the results of Cunningham and himself with those of Poincaré and the leading German relativists:
According to the general principles of group-theory, the quantities and relations which are invariant with regard to the principal group should represent true physical quantities and relations. Some of these invariants for the group have been found by Einstein, Poincaré, Minkowski, Planck, Cunningham and the author.7373endnote: 73 The transformations of the 15-parameter group of conformal transformations correspond to what Bateman called the “spherical wave transformations.” On the Bateman-Cunningham discovery of the covariance of Maxwell’s equations under , see Rowe (1999, 211), and Kastrup (2008). It is desirable that all the principal invariants and covariants for the group should be found, for then we shall perhaps be able to decide whether Einstein’s conditions of observation are the right ones or not. (Bateman 1912, 340)
Bateman’s accomplishment was duly recognized by Philipp Frank (1884–1966), with whom he probably crossed paths in Göttingen in 1906. Frank (1911) described the covariance of the Maxwell equations under the Lorentz group as “one of the most important mathematico-physical facts of modern physics,” and identified Lorentz, Minkowski, and Bateman as the principal investigators in this area of study, to which he and the Viennese mathematician Hermann Rothe (1882–1923) were active contributors, along with von Ignatowsky.
In a wide-ranging review of the consequences of relativity theory for the philosophy of space and time, Bateman drew on Ribaucour’s transformations of spheres; his idea was to investigate the “physical aspect of time in order to understand the idea of simultaneity” (Bateman, 1910a, 2). In what Bateman called a “view”, an ordered pair of spheres represents a four-vector, the components of which are differences of spatial coordinates and radii. Four-vector magnitude is given by the length of a shared tangent, such that that a null vector corresponds to spheres in contact.
By considering Ribaucour’s spheres as light spheres, Bateman demonstrated the relativity of simultaneity and the impossibility of hyperlight velocities. Bateman’s depiction of a light source in uniform translation (Fig. 13) features four non-concentric light spheres. His figure differs little from that employed by Poincaré in 1906–1907 (Fig. 3); only the direction of motion is reversed. Imagining a space filled with light-synchronized clocks, Bateman argued with respect to his diagram that the wave-front of only one light sphere may pass through a given point at a given time, such that behavior of light-waves makes manifest the simultaneity relation.
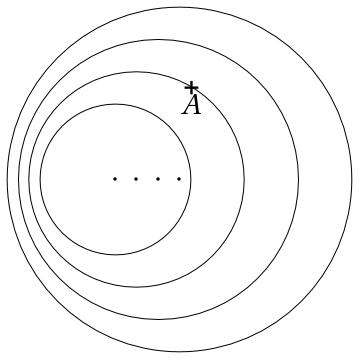
In subsequent papers, Bateman neglected to discuss or apply his diagrammatic interpretation of four-vectors, which quickly fell from view. A similar interpretation of four-vectors, proposed by a professor of descriptive geometry in Braunschweig, H. E. Timerding (1912; 1915), fared no better. Few theorists in Britain were then familiar with four-vectors, and consequently, few were in a position to grasp the full meaning of Bateman’s potent image of tangent spheres. Bateman’s illustration of the Einstein simultaneity relation was thereby less comprehensible to his contemporaries than the simpler one concocted by Laue, which involved only a passing knowledge of plane geometry.
9 Light-figure skepticism
More than a few physicists felt that the grounds for accepting light-sphere covariance as the foundation of relativity were not compelling. For example, as mentioned above, A. H. Bucherer saw no need to adopt Einstein’s view of the light sphere. This section takes up the cases of two light-figure skeptics, which is to say, physicists who contested the epistemic priority accorded by Einstein to lightwaves: Emil Wiechert (1861–1928) and Waldemar von Ignatowsky (1875–1943).
Minkowski’s colleague in Göttingen, the geophysicist Emil Wiechert admired Minkowski’s theory, but like many scientists, he remained attached to the notion of an ether. Wiechert’s ether was attached by stipulation to an inertial frame, and was entirely consistent, in his view, with Minkowski’s spacetime theory (Wiechert 1911, 757). In an essay entitled “The principle of relativity and the ether”, Wiechert held that both sound waves and light waves that are spherical in one (absolute) frame are flattened in the direction of motion of an observer translating with respect to this frame. Even if Wiechert granted that Einstein was the first to develop a “rigorous understanding of Lorentz covariance”, and to understand the conventional nature of distant simultaneity, he did not feel compelled to adopt Einstein’s kinematics.7474endnote: 74 Wiechert to Lorentz, 9 March 1912, in Kox (2008, 359); Wiechert (1911, 756). In a review of Wiechert’s theory, Laue (1912) found fault with his logic, but he admitted with Wiechert that the question of the existence of an absolute frame belonged to philosophy, not to physics.
Like Wiechert, von Ignatowsky admired Minkowski’s spacetime theory, but was dissatisfied with Einstein’s relativity. In particular, Einstein’s light postulate seemed unobvious to him. Nonetheless, he was impressed by how the light constant appeared in Minkowskian relativity to be “more a universal spacetime constant than the speed of light” (von Ignatowsky 1910, 793).7575endnote: 75 Born in Tiflis (Tbilisi, Georgia), von Ignatowsky earned a Ph.D. in physics at the University of Giessen in 1909, and found employment with the Leitz optical firm in Wetzlar (Klein et al. 1993, 251). What von Ignatowsky sought to derive were coordinate transformations that guarantee relativity of inertial frames, but do not depend on the light postulate. Introducing the usual constraints, and denoting by a differential quotient depending on position , time , and velocity , he found (in modified notation):7676endnote: 76 On von Ignatowsky’s transformation see Jammer (1979, 215), Torretti (1996, 76), Brown (2005, 105), and Darrigol (2014, 139).
| (17) |
where is a universal constant, such that
| (18) |
In order to determine the value of the constant , von Ignatowsky considered the equipotential surface of a point-charge in uniform motion. For a comoving observer, the equipotential surface has the form of a sphere, but for an observer at rest, the equipotential surface is described by a Heaviside-ellipsoid. In other words, for an observer at rest, the equipotential surface is a rotational ellipsoid, the longitudinal and transverse axes of which are related by . Von Ignatowsky’s transformation requires that a spherical surface attached to the comoving observer’s frame transform to a flattened ellipsoid in the frame of an observer at rest, such that
| (19) |
Consequently, , such that both and are now universal constants. Von Ignatowsky’s identification of as a universal constant depends on the form of the equipotential surface, a form independent of the principle of relativity, as von Ignatowsky was careful to point out.7777endnote: 77 On the relation between Lorentz contraction and the Heaviside ellipsoid, see Hunt (1988).
Von Ignatowsky noted in passing that represents the “speed of one of our worlds,” i.e., one of “unendlessly many reference frames.” While the latter description recalls Cunningham’s multiple-ether view of relativity (§ 2), it is more likely an additional echo of Minkowski’s Cologne lecture. In a final tribute to Minkowski’s spacetime realism, von Ignatowsky concluded his derivation with the following credo:7878endnote: 78 “Nun dürfen wir aber unter einem Ruhekoordinatensystem nicht etwa nur ein mathematisches Gebilde verstehen, sonder müssen uns dabei eine materielle Welt mit ihren Beobachtern und synchronem Uhren denken.”
Now we should not consider an inertial coordinate system as something like a mere mathematical entity, but we must instead think of it as a material world with its observers and synchronized clocks. (von Ignatowsky 1910, 794)
Although von Ignatowsky drew freely on Minkowskian language and imagery, he did not adopt Minkowski’s four-dimensional calculus, preferring to rewrite the latter’s four-dimensional “vectors of the first and second type” in the form of ordinary three-vectors. More than likely, this was a choice guided by his recent investment in three-dimensional vector analysis, in the form of a book (von Ignatowsky 1909) published in Eugen Jahnke’s Teubner collection “Mathematisch-Physikalische Schriften für Ingenieure und Studierende.”
Wiechert and von Ignatowsky were uneasy with the special evidentiary status accorded by Einstein to light signals, as reflected in their approaches to relativity. Wiechert’s rejection of Einstein’s radical reform of kinematics found inspiration in Minkowski’s spacetime theory, in virtue of the absolute nature of the direction of a particle’s four-velocity (Wiechert 1911, 757). Von Ignatowsky’s admiration for Minkowski’s geometric interpretation of the light-constant , and concomitant rejection of the latter’s four-dimensional formalism suggest that one could accomodate a Minkowskian ontology, while rejecting Minkowskian formalism, which is to say, the precise opposite of what Laue advised in his textbook (Walter 2010).
10 Discussion
Introduced without fanfare by Einstein in connection with his postulates of relativity and universal lightspeed invariance, the notion of light-sphere covariance engaged the imagination of theorists and experimentalists alike. A rival light-shell theory was soon proposed, in the form of Poincaré’s light-ellipsoid and assorted two-dimensional diagrams. At the time, Poincaré’s theory of the light-ellipsoid had much to recommend it, including a privileged coordinate frame, and a simple diagram-based derivation of the Lorentz transformation. Poincaré did not seek to publish his derivation, however, and soon Cunningham and Einstein published their own equally-elementary algebraic derivations of the Lorentz transformation, based on light-sphere covariance.
Einstein’s kinematics lacked a visually-intuitive model until 1908, when Minkowski proposed a model of spacetime that subtended an elementary geometric derivation of the Lorentz transformation, albeit a derivation that Minkowski did not see fit to publish himself. Minkowski did not discuss the light sphere directly, either. Instead, he presented the Lorentz-covariance of the light-wave equation as a compelling formal argument in favor of his four-dimensional approach to physics, and cast light-sphere covariance in four-dimensional language, introducing the lightcone structure of spacetime. His expression of the Lorentz transformation as a matrix inspired investigations by Cunningham and Bateman of the conformal covariance of Maxwell’s equations, which suggested the possibility of a generalization of the principle of relativity to frames in non-inertial motion. The lightcone itself inspired Robb’s theory of space and time, intended originally as an alternative to Einsteinian relativity.
The idea of light-sphere covariance travelled across both national and disciplinary boundaries, being carried initially by journals of physics, philosophy, and general science in Germany and Great Britain. When Max Laue wrote his treatise on the principle of relativity (1911a), he passed over the contributions of Cunningham and Bateman, and drew instead on the work of a fellow German Privatdozent, Otto Berg. Cunningham and Bateman were colleagues for a year, while Bateman and Laue heard lectures by Hilbert and Minkowski in Göttingen. All of these scientists were young men; only Berg had passed thirty. None held a permanent university position at the time of the contributions studied here, and all but Berg went on to obtain academic appointments.7979endnote: 79 Berg went to work for the Siemens-Halske engineering firm in Berlin, where he co-discovered element seventy-five (Rhenium) with Walter Noddack and Ida Tacke.
According to the recollections of Philipp Frank (1947, 206), Einstein remarked to him that he could “hardly understand Laue’s book.” Frank read Einstein’s comment as a reflection on the mathematical sophistication of Laue’s treatise, but the mathematics employed by Laue were certainly not new to Einstein. In light of the several contributions to relativity theory and the theory of the electron after 1905 reviewed in this chapter, I suggest an alternative reading of Einstein’s offhand comment to Frank on Laue’s treatise: Einstein found the content of Laue’s book to stem in large part from the work of others; as such, for Einstein Laue’s book was not incomprehensible, just foreign to his own way of thinking about relativity.
Although the concept of light-sphere covariance crossed national and disciplinary boundaries with apparent ease, it did not meet with universal assent. There were those, like Bucherer, who found Einstein’s argument in favor of light-sphere covariance to be unconvincing. The special evidentiary status assigned to the behavior of lightwaves in Einstein’s theory troubled physicists like von Ignatowsky and Wiechert, who sought to treat electromagnetic waves in the same manner as other propagation phenomena. The case of Poincaré and Robb is particularly instructive in this regard, in that they both shared Einstein’s high epistemic regard for lightwaves, but deplored – for different philosophical reasons – Einstein’s metric interpretation of the light sphere.
Four decades after the events described in this chapter, Laue wrote about the “somewhat excessive polemic” against relativity as a consequence of “lack of insight” on the part of the theory’s opponents (Laue 1947, 68). The form of a light pulse for moving observers was a topic about which leading theorists disagreed, as we have seen. Laue also recalled a “decisive turn” for relativity theory, triggered by Einstein’s view of the equal epistemic value of space and time measurements among inertial frames of reference. Closely related to Einstein’s belief, the derivation of the Lorentz transformation via covariance of the light-sphere equation stabilized interpretations of the transformation along Einsteinian lines, and contributed powerfully to the emergence of a unified doctrine of the physics of inertial frames. One consequence of this movement was a heightened recognition of Einstein as the principal architect of the theory of relativity, as expressed by Laue’s 1911 treatise and its six re-editions.
Acknowledgments
Key points of this paper were elaborated in discussions with Olivier
Darrigol, Tilman Sauer, June Barrow-Green, and David Rowe; their help
is much appreciated. The paper benefits from the expert assistance of
Kathryn McKee and Fiona Colbert of St. John’s College, whom I thank
most kindly. Citations of the Joseph Larmor Correspondence are by
permission of the Master and Fellows of St. John’s College,
Cambridge. Permission to quote from the Council Minutes of the London
Mathematical Society is gratefully acknowledged.
I thank the Niedersächsiche Staats- und
Universitätsbibliothek Göttingen for authorizing
publication of the diagram in Fig. 9. I am
grateful for the support of the Dibner Rare Book and Manuscript
Library, and to its staff members Lilla Vekerdy and Kirsten van der
Veen for their able assistance during my residence in 2013. A
preliminary version of the paper was published in 2011 on
PhilSci-Archive.
Notes
- 1 For gradualist views of the acceptance of relativity theory see Hirosige (1968), Miller (1981), and Darrigol (1996, 2000).
- 2 On the assumption of linearity, see Brown (2005, 26), and for the kinematic background to Einstein’s first paper on relativity, see Martínez (2009). Einstein did not let kinematics decide the matter once and for all in 1905. In a letter of September 1918 written to his friend, the anti-relativist and political assassin Friedrich Adler, Einstein considered the global factor in the Lorentz transformation to be of an empirical nature, whose value had been determined (to Einstein’s satisfaction) by the results of certain electron-deflection experiments (Walter 2009, 213). Poincaré expressed his views to Lorentz by letter in May 1905; see Walter, Bolmont, and Coret, eds, 2007b, §§ 38.4, 38.5.
- 3 On the compatibility argument, see Williamson (1977). Gaps in Einstein’s reasoning are apparent from a modern standpoint; see, for example, Kennedy (2005).
- 4 Sommerfeld to H.A. Lorentz, 26 Dec. 1907, in Kox, ed. (2008, § 165).
- 5 For an assessment of Baker’s rise to prominence among Cambridge geometers, see Barrow-Green and Gray (2006).
- 6 See McCrea (1978), and John Heilbron’s interview with Cunningham (1963).
- 7 A proponent of Einstein’s theory is understood here to be an individual seeking either to support or to extend any of the novel ideas contained in Einstein’s 1905 paper. On the British reception of relativity, see Goldberg (1970), Sánchez-Ron (1987), and Warwick (2003).
- 8 See Goldberg (1970), and Hunt (1986).
- 9 Cunningham noted a personal communication with Larmor, to the effect that while a proof of the Lorentz transformation’s validity for electron theory to second order of approximation in appeared in the latter’s Æther and Matter (1900), Larmor had “known for some time that [the Lorentz transformation] was exact” (Cunningham 1907, 539).
- 10 Cunningham (1912) recalled this fact, without mentioning Neumann.
- 11 Cunningham’s conclusion agrees with that reached later by Fermi; see Rohrlich (2007, 17), Janssen and Mecklenburg (2006).
- 12 Cunningham (1907, 547). Both Cunningham and Planck failed to understand Bucherer’s theory, which allowed for closed links between electrons; see Darrigol (2000, 371).
- 13 According to Balàsz (1972), Bucherer’s remark shows that he was “confused about the basic problem of relativity”, in that he failed to “realize the connection of this problem with the Michelson-Morley experiment and its relation to the transformation laws.” Yet the Lorentz-FitzGerald contraction explains on its own the null result of the Michelson-Morley experiment, as Bucherer and contemporary theorists knew quite well.
- 14 See Einstein (1908, § 3); reed. in Stachel et al., eds. (1989, vol. 2, Doc. 47). Cunningham’s paper appeared in the October 1907 issue of the Philosophical Magazine, and Einstein’s review article was submitted for publication in Johannes Stark’s Jahrbuch der Radioaktivität und Elektronik on 4 December 1907.
- 15 An alternative approach, advanced by Max Born (1909), involved redefining the notion of a rigid body in Minkowski spacetime. On related developments, see Maltese and Orlando (1995).
- 16 Sommerfeld insisted in his lectures on electrodynamics that a Lorentz transformation does not change a “Lichtkugel” into a “Lichtellipsoid” (Sommerfeld 1948, 236).
- 17 See the edition of Henri Vergne’s notes of Poincaré’s 1906–1907 lectures at the Paris Faculty of Science (Chopinet, 1953), and his 1912 lectures at the École supérieure des postes et télégraphes (Poincaré 1913), along with the two articles (Poincaré 1908a, 1909). The article of 1908 was reedited by Poincaré in Science et méthode (1908b); the light ellipse is described on p. 239, but the diagram was suppressed from this version, presumably by the editor, Gustave Le Bon.
- 18 See Lémeray (1912), communicated to the Paris Academy of Sciences on 9 December, 1912, and the retraction (ibid., p. 1572). It is not clear whether Lémeray meant to attribute a flattened light-ellipsoid or an elongated light-ellipsoid to Einstein. Several years later, the Swiss physicist Édouard Guillaume (1921) referred to an “ellipsoïde de Poincaré”. Guillaume corresponded with Einstein on this topic; see Kormos Buchwald (2006, Doc. 241).
- 19 See Langevin’s notes of Poincaré’s lectures, Fonds Langevin, box 123, Bibliothèque de l’École supérieure de physique et de chimie industrielle, Paris.
- 20 For details on Langevin’s paper, see Miller (1973).
- 21 See Langevin’s notebook, box 123, and letter to his wife of 26 September, 1904, box 3, Fonds Langevin, Library of the École supérieure de physique et de chimie industrielle, Paris.
- 22 On Hertz’s solution, see Darrigol (2000, 251).
- 23 Henri Vergne, notebook 2, CAPHI, University of Nantes.
- 24 Poincaré’s fantasy was extended by Richard Tolman (1914) via dimensional analysis, in the form of a “principle of similitude”, a view that attracted sharp criticism from Percy Bridgman (1916).
- 25 The notion of an absolutely-resting frame remained an abstraction for Poincaré. In 1912, he upheld the conventionality of spacetime, and expressed a preference for Galilei spacetime over Minkowski spacetime (Walter 2009).
- 26 See Poincaré (1901, 536), where the value is off by a factor of ten. In a later essay, Poincaré (1904, 312) supplied the “correct” value of the correction factor for terrestrial observers and an ether at rest with respect to the Sun, where .
- 27 The published version of the notes differs markedly from the original, suggesting that their editor, the astronomer Marguerite Chopinet, disagreed with their content; cf. Chopinet (1953, 219).
- 28 “Alors je prends une surface rigoureusement spherique. Je la mesure avec mon mètre: dans la direction du mouvement mon mètre sera contracté de ; sa longueur vraie sera devenue . Donc mon diamètre dans le sens du mouvement aura pour longueur mesurée . Dans le sens perpendiculaire la longueur mesurée sera 1. Donc une sphère paraîtra un ellipsoïde allongé dans le sens du mouvement.”
- 29 Using the relations specified in Fig. 2, we have Rearranging the latter expression in terms of , we find , and substituting the value of from (4) we obtain Poincaré’s expression (5) for apparent time .
- 30 The context of Poincaré’s invitation to Göttingen is discussed in Walter (2018).
- 31 On Poincaré’s engagement with electrotechnology, and wireless telegraphy in particular, see Galison (2003), Gray (2013), and Walter (2017).
- 32 One may wonder why the watch in Poincaré’s thought experiment runs fast, and not slow, as would be required by time dilation in an Einsteinian or Minkowskian context. An explanation is at hand, if we focus on the first observer’s experience. At first, he believes he has a certain velocity, say 200km/s. An exchange of telemetry data with the second observer convinces him that he is moving slower than he thought previously. One way for him to account for this revision is to admit that his watch is running fast. Other explanations for the fast watch can be imagined; see Walter (2014).
- 33 “…un théorème de géométrie très simple montre que le temps apparent que la lumière mettra à aller de en , c’est-à-dire la différence entre le temps local en au moment du départ de , et le temps local en au moment de l’arrivée en , que ce temps apparent, dis-je, est le même que si la translation n’existait pas, ce qui est bien conforme au principe de relativité.”
- 34 An excerpt of the Revue article was included in Poincaré’s Science et méthode (Poincaré, 1908b), neglecting mathematical details, such as Poincaré’s discussion of relative velocity.
- 35 For a sketch of the French reception of relativity, see Walter (2011).
- 36 Despite Lorentz’s embrace of the what Louis du Pasquier called the “principle of lightwave sphericity”, the Swiss mathematician later wrote that Lorentz rejected this principle (Du Pasquier 1922, 68).
- 37 On Guillaume’s collaboration with Einstein, see Einstein’s letter to Jacob Laub, 20 March, 1909, in Klein (1993, Doc. 143).
- 38 A displacement from one point to another on the light ellipse corresponds to a Lorentz transformation in this interpretation. The radii from a focus to any two points of the ellipse are related by a rotation and, in general, a dilation or a contraction.
- 39 On Poincaré’s models of hyperbolic geometry, see Gray (1989) and Zahar (1997).
- 40 For background, see Walter (1999a; 2008).
- 41 On the rise of Göttingen as a scientific center, see Manegold (1970) and Rowe (1989).
- 42 See Frank (1947, 206). Miller (1976, 918) emphasizes the relative simplicity of the mathematical tools deployed by Einstein in his relativity paper, in comparison to those Poincaré brought to bear on similar problems. Renn (2007b, 69) observes that Einstein’s uncanny aptitude for informal analysis of complex problems served him well in both special and general relativity.
- 43 Minkowski’s visually-intuitive approach to relativity is explored at length by Galison (1979).
- 44 On Minkowski’s use of hyperbolic geometry in this lecture, see Reynolds (1993).
- 45 “Werden jedoch vier Raumpunkte, die nicht in einer Ebene liegen, zu einer und derselben Zeit aufgefaßt, so ist es nicht mehr möglich, durch eine Lorentz-Transformation eine Abänderung des Zeitparameters vorzunehmen, ohne daß der Charakter der Gleichzeitigkeit dieser vier Raum-Zeitpunkt verloren” (Minkowski 1908, 69).
- 46 See Born (1909, 9; 1959, 503). For further references and details on Minkowski’s distortion and its reception, see Walter (1999a).
- 47 NSUB Handschriftenabteilung. The demonstration missing from the published text of Minkowski’s lecture was later supplied by Arnold Sommerfeld, in an editorial note to his friend’s lecture. The annotated version of the lecture appeared in an anthology of papers on the theory of relativity edited by Otto Blumenthal (1913). According to Rowe (2009, 37), Sommerfeld was the driving force behind the latter anthology.
- 48 As seen above, Poincaré also derived the Lorentz transformation from the assumption of Lorentz contraction of concrete rods, and the isotropy of light propagation for inertial observers. He later considered (apparent) time deformation as a consequence of the principle of relativity and Lorentz contraction; see (Poincaré 1913, 44).
- 49 Tanner (1917, 571). I thank J. Barrow-Green for pointing me to this source.
- 50 Robb was admitted to the Society on 27 Nov. 1905 (Proceedings of the Cambridge Philosophical Society 16, 1912, p. 16).
- 51 Robb to Larmor, 6 March 1904, Larmor Papers, St. John’s College Library; Lorentz (1909, 115). Voigt sent Lorentz a copy of Robb’s dissertation; see Lorentz to Voigt, 18 Dec. 1904, in Kox (2008, § 121).
- 52 In a letter to Larmor of 18 Jan. 1911, the Cambridge mathematician A. E. H. Love wrote that he had “noted explicitly in writing” to Robb that one of his formulas was from Lobachevski geometry, and that “space might be saved by bringing this fact in” (Larmor Papers, St. John’s College Library). On Robb’s use of hyperbolic geometry, see Walter (1999b).
- 53 For Robb the “appearance” of contraction was a necessary consequence of light time-of-flight measurements. Robb, Einstein, and their contemporaries focused on the instantaneous form of moving objects, in an approach distinct from the one adopted in the late 1950s. The latter studies characterized what Roger Penrose (1959) referred to as the “photographic” appearance of a moving object.
- 54 Robb (1911, 1), original emphasis. Cf. Poincaré, Science and Hypothesis (1905a, 50).
- 55 For appreciations of Robb’s geometry, see Briginshaw (1979), and Cat (2016).
- 56 LMS Council Minutes, 10 Nov. 1910, LMS archives.
- 57 Love to Larmor, 18 Jan. 1911, op. cit. Sedleian Chair of Natural Philosophy at Oxford since 1899, Love was Secretary (i.e., managing editor) of the LMS from 1890 to 1910.
- 58 Jahrbuch über die Fortschritte der Mathematik 43, 1911, p. 559. A succinct summary of Robb’s index concept is provided by Barrow-Green and Gray (2006).
- 59 LMS Council Minutes, 9 Feb. 1911, LMS archives.
- 60 Cunningham (1914, 87–89); for an analysis of the procedure, see Newman & Price (2010).
- 61 See Cunningham (1910, 79). As for Bateman, he credited Cunningham with the discovery of the conformal transformations of the equations of electrodynamics; see Bateman (1910c, 224).
- 62 L’Enseignement mathématique 10 (1908), 336; Bateman to Hilbert, 1909, Nachlass Hilbert 13, Handschriftenabteilung, NSUB Göttingen.
- 63 See Minkowski (1909), where the Lorentz transformation is attributed to a paper published in 1887 by Voigt. Minkowski described the covariance of the differential equation of light-wave propagation as the “impetus and true motivation” for assuming the covariance of all laws of physics with respect to the transformations of the Lorentz group (p. 80).
- 64 See Bateman (1908, 629), read 8 Sept. 1908. No mention is made in this paper of the source of the transformations, but a subsequent work by Bateman credits Cunningham with the “discovery of the formulæ of transformation in the case of an inversion in the four-dimensional space,” and cites papers by Hargreaves and Minkowski employing a four-dimensional space with one imaginary axis (Bateman 1909, 224, communicated 9 Oct. 1908). Minkowski’s paper (1908, published 5 April 1908) was cited by both Cunningham and Bateman. Remarked first by Whittaker (1953, 195), the significance of Minkowski’s spacetime theory for the contributions of Cunningham and Bateman is contested by Warwick (2003, 423 n. 49). On the “light-geometric approach” to the foundations of relativity by Cunningham and Bateman, see Jammer (1979, 222).
- 65 For example, see Warwick (2003, 421) and Bromwich (1901).
- 66 Laue (1961, XVIII–XXI); Laue to Margot Einstein, 23 Oct. 1959, cited by Holton (1965, 39).
- 67 Laue (1911b); Janssen & Mecklenburg (2006).
- 68 Laue (1952).
- 69 See Max Born’s review in Physikalische Zeitschrift (1912).
- 70 On Laue’s portrayal of Einstein’s contribution, see Staley (1998). Laue’s contributions to relativity are detailed by Norton (1992) and Rowe (2008).
- 71 Planck’s argument, which builds on that of Einstein (see above, § 2), has inspired many textbook authors. For an example employing a spherical array of photomultipliers at rest in two inertial frames in relative motion, see Rosser (1967, 76).
- 72 Laue’s use of primes in his light-sphere diagram is peculiar, but is reproduced intact in Fig. 12, in keeping with the first four editions of his textbook (up to 1921). In the sixth edition (1955, 29), , , and are all unprimed, and the primed symbols are as expected: and .
- 73 The transformations of the 15-parameter group of conformal transformations correspond to what Bateman called the “spherical wave transformations.” On the Bateman-Cunningham discovery of the covariance of Maxwell’s equations under , see Rowe (1999, 211), and Kastrup (2008).
- 74 Wiechert to Lorentz, 9 March 1912, in Kox (2008, 359); Wiechert (1911, 756).
- 75 Born in Tiflis (Tbilisi, Georgia), von Ignatowsky earned a Ph.D. in physics at the University of Giessen in 1909, and found employment with the Leitz optical firm in Wetzlar (Klein et al. 1993, 251).
- 76 On von Ignatowsky’s transformation see Jammer (1979, 215), Torretti (1996, 76), Brown (2005, 105), and Darrigol (2014, 139).
- 77 On the relation between Lorentz contraction and the Heaviside ellipsoid, see Hunt (1988).
- 78 “Nun dürfen wir aber unter einem Ruhekoordinatensystem nicht etwa nur ein mathematisches Gebilde verstehen, sonder müssen uns dabei eine materielle Welt mit ihren Beobachtern und synchronem Uhren denken.”
- 79 Berg went to work for the Siemens-Halske engineering firm in Berlin, where he co-discovered element seventy-five (Rhenium) with Walter Noddack and Ida Tacke.
References
- Theorie der Elektrizität 2: Elektromagnetische Theorie der Strahlung. Teubner, Leipzig. External Links: Link Cited by: §2.
- The acceptability of physical theories: Poincaré versus Einstein. In General Relativity: Papers in Honour of J. L. Synge, L. O’Raifeartaigh (Ed.), pp. 21–34. Cited by: endnote 13.
- Geometry at Cambridge, 1863–1940. Historia Mathematica 33 (3), pp. 315–356. Cited by: endnote 5, endnote 58.
- On conformal transformations of a space of four dimensions and their application to geometrical optics. Report–British Association 78, pp. 627–629. Cited by: endnote 64.
- The conformal transformations of a space of four dimensions and their applications to geometrical optics. Proceedings of the London Mathematical Society 7, pp. 70–89. Cited by: §8, endnote 64.
- The physical aspect of time. Memoirs and Proceedings, Manchester Literary and Philosophical Society 54 (14), pp. 1–13. Cited by: Figure 13, §8.
- The relation between electromagnetism and geometry. Philosophical Magazine 20, pp. 623–628. Cited by: §8.
- The transformations of the electrodynamical equations. Proceedings of the London Mathematical Society 8 (1050), pp. 223–264. Cited by: endnote 61.
- Some geometrical theorems connected with Laplace’s equation and the equation of wave motion. American Journal of Mathematics 34, pp. 325–360. Cited by: §8, §8.
- Das Relativitätsprinzip der Elektrodynamik. Abhandlungen der Fries’schen Schule 3, pp. 333–382. Cited by: §8.
- Durée et simultanéité : à propos de la théorie d’Einstein. Alcan, Paris. Cited by: §5.
- Das Relativitätsprinzip; Eine Sammlung von Abhandlungen. Teubner, Leipzig. External Links: Link Cited by: endnote 47, A. Sommerfeld (1913).
- Mathematical Correspondences and Critical Editions. Springer, Cham. External Links: Document Cited by: S. A. Walter (2018).
- Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips. Annalen der Physik 335, pp. 1–56. Cited by: endnote 15, endnote 46.
- Besprechung von Max Laue, Das Relativitätsprinzip. Physikalische Zeitschrift 13, pp. 175–176. Cited by: endnote 69.
- Besprechung von Max Weinstein, Die Physik der bewegten Materie und die Relativitätstheorie. Physikalische Zeitschrift 15, pp. 676. Cited by: §6.
- Die Relativitätstheorie Einsteins und ihre physikalischen Grundlagen. Springer, Berlin. Cited by: Figure 8.
- Erinnerungen an Hermann Minkowski zur 50. Wiederkehr seines Todestages. Naturwissenschaften 46 (17), pp. 501–505. Cited by: §6, endnote 46.
- Tolman’s principle of similitude. Physical Review 8, pp. 423–431. Cited by: endnote 24.
- The axiomatic geometry of space-time: an assessment of the work of A. A. Robb. Centaurus 22 (4), pp. 315–323. Cited by: endnote 55.
- Conformal space transformations. Proceedings of the London Mathematical Society 33 (749), pp. 185–192. Cited by: endnote 65.
- Physical Relativity: Space-Time Structure from a Dynamical Perspective. Oxford University Press, Oxford. Cited by: endnote 2, endnote 76.
- On a new principle of relativity in electromagnetism. Philosophical Magazine 13, pp. 413–420. Cited by: §2.
- Messungen an Becquerelstrahlen; die experimentelle Bestätigung der Lorentz-Einsteinschen Theorie. Physikalische Zeitschrift 9 (22), pp. 755–762. External Links: Link Cited by: §1.
- On the principle of relativity and on the electromagnetic mass of the electron; a reply to Mr. E. Cunningham. Philosophical Magazine 15, pp. 316–318. Cited by: §2.
- From Maxwell to Microphysics. University of Chicago Press, Chicago. External Links: Link Cited by: §8.
- Images and logic of the light cone: tracking Robb’s postulational turn in physical geometry. Revista de Humanidades de Valparaiso 4 (8), pp. 43–105. External Links: Link Cited by: endnote 55.
- Henri Poincaré, Les limites de la loi de Newton. Bulletin astronomique 17 (3), pp. 121–269. External Links: Link Cited by: endnote 17, endnote 27.
- On the electromagnetic mass of a moving electron. Philosophical Magazine 14, pp. 538–547. External Links: Link Cited by: §2, §2, endnote 12, endnote 9.
- The principle of relativity in electrodynamics and an extension thereof. Proceedings of the London Mathematical Society 8, pp. 77–98. Cited by: §8, endnote 61.
- The principle of relativity. Report–British Association 81, pp. 236–245. External Links: Link Cited by: endnote 10.
- The Principle of Relativity. Cambridge University Press, Cambridge. External Links: Link Cited by: §7, §8, endnote 60.
- A History of Relativity: The Role of Henri Poincaré and Paul Langevin. Ph.D. Thesis, Yeshiva University, New York. Cited by: §5.
- Henri Poincaré’s criticism of fin de siècle electrodynamics. Studies in History and Philosophy of Modern Physics 26, pp. 1–44. Cited by: §5.
- The electrodynamic origins of relativity theory. Historical Studies in the Physical and Biological Sciences 26 (2), pp. 241–312. Cited by: endnote 1.
- Electrodynamics from Ampère to Einstein. Oxford University Press, Oxford. External Links: Link Cited by: §2, endnote 1, endnote 12, endnote 22.
- Physics and Necessity: Rationalist Pursuits from the Cartesian Past to the Quantum Present. Oxford University Press, Oxford. Cited by: endnote 76.
- Poincaré and light. See Henri Poincaré, 1912–2012, Duplantier and Rivasseau, Progress in Mathematical Physics, Vol. 67, pp. 1–50. Cited by: §5.
- Henri Poincaré, 1912–2012. Springer, Berlin. Cited by: O. Darrigol (2015).
- Zur Elektrodynamik bewegter Körper. Annalen der Physik 322, pp. 891–921. External Links: Link Cited by: Figures of Light in the Early History of Relativity (1905–1914) Published in David Rowe, Tilman Sauer, and Scott A. Walter, eds, Beyond Einstein: Perspectives on Geometry, Gravitation, and Cosmology in the Twentieth Century (Einstein Studies 14), 3–50, Basel: Birkhäuser, 2018; doi: 10.1007/978-1-4939-7708-6_1, §1, §2, §2, §3, §3.
- Relativitätsprinzip und die aus demselben gezogenen Folgerungen. Jahrbuch der Radioaktivität und Elektronik 4, pp. 411–462. Cited by: endnote 14.
- Das Verhalten der elektromagnetischen Feldgleichungen gegenüber linearen Transformationen. Annalen der Physik 340, pp. 599–607. External Links: Link Cited by: §8.
- Einstein: His Life and Times. Knopf, New York. External Links: Link Cited by: §10, endnote 42.
- Minkowski’s spacetime: from visual thinking to the absolute world. Historical Studies in the Physical Sciences 10, pp. 85–121. Cited by: endnote 43.
- Einstein’s Clocks and Poincaré’s Maps: Empires of Time. Norton, New York. Cited by: endnote 31.
- The Comparative Reception of Relativity. Reidel, Dordrecht. Cited by: J. M. Sánchez-Ron (1987).
- The Expanding Worlds of General Relativity. Birkhäuser, Boston/Basel. Cited by: S. A. Walter (1999a).
- In defense of Ether: the British response to Einstein’s special theory of relativity 1905–1911. Historical Studies in the Physical Sciences 2, pp. 89–125. Cited by: §2, endnote 7, endnote 8.
- Ideas of Space: Euclidean, Non-Euclidean and Relativistic. Clarendon, Oxford. Cited by: endnote 39.
- The Symbolic Universe: Geometry and Physics, 1890–1930. Oxford University Press, Oxford. Cited by: D. E. Rowe (1999), S. A. Walter (1999b).
- Henri Poincaré: A Scientific Biography. Princeton University Press, Princeton. External Links: Link Cited by: endnote 31.
- Expression mono et polyparametrique du temps dans la theorie de la relativité. See Comptes rendus du Congrès international des mathématiciens : Strasbourg, 22–30 septembre 1920, Villat, pp. 594–602. Cited by: endnote 18.
- Un résultat des discussions de la théorie de la relativité d’Einstein au Collège de France. Revue générale des sciences pures et appliquées 33, pp. 322–324. Cited by: §5.
- The Significance of the Hypothetical in the Natural Sciences. Walter de Gruyter, Berlin. External Links: Document Cited by: S. A. Walter (2009).
- Interview with Dr. Ebenezer Cunningham. Archives for the History of Quantum Physics. External Links: Link Cited by: endnote 6.
- The Dilemmas of an Upright Man: Max Planck as Spokesman for German Science. University of California Press, Berkeley. External Links: Link Cited by: §1.
- Interactions: Mathematics, Physics and Philosophy, 1860–1930. Springer, Dordrecht. Cited by: M. Janssen and M. Mecklenburg (2006).
- Theory of relativity and the ether. Japanese Studies in the History of Science 7, pp. 37–53. Cited by: endnote 1.
- The metaphor of space-time events in science. Eranos Jahrbuch 34, pp. 33–78. Cited by: endnote 66.
- Experimenting on the ether: Oliver J. Lodge and the great whirling machine. Historical Studies in the Physical Sciences 16 (1), pp. 111–134. External Links: Link, Document Cited by: endnote 8.
- The origins of the FitzGerald contraction. British Journal for the History of Science 21 (1), pp. 67–76. Cited by: endnote 77.
- Die Vektoranalysis und Anwendung in der theoretischen Physik. Teubner, Leipzig/Berlin. Cited by: §9.
- Einige allgemeine Bemerkungen zum Relativitätsprinzip. Berichte der Deutschen Physikalischen Gesellschaft 12 (20), pp. 788–796. Cited by: §9, §9.
- Some foundational problems in the special theory of relativity. In Problems in the Foundations of Physics, G. Toraldo di Francia (Ed.), Proceedings of the International School of Physics “Enrico Fermi”, Vol. 72, pp. 202–236. Cited by: endnote 64, endnote 76.
- From classical to relativistic mechanics: electromagnetic models of the electron. See Interactions: Mathematics, Physics and Philosophy, 1860–1930, Hendricks et al., pp. 65–134. Cited by: endnote 11, endnote 67.
- Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein, Volume 1: The Torch of Mathematics, 1800–1870. University of Chicago Press, Chicago. Cited by: §6.
- Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein, Volume 2: The Now Mighty Theoretical Physics, 1870–1925. University of Chicago Press, Chicago. Cited by: §6.
- On the advancements of conformal transformations and their associated symmetries in geometry and theoretical physics. Annalen der Physik 17 (9), pp. 691–704. Cited by: endnote 73.
- On Einstein’s 1905 electrodynamics paper. Studies in History and Philosophy of Modern Physics 36 (1), pp. 61–65. Cited by: endnote 3.
- The Collected Papers of Albert Einstein, Volume 5, The Swiss Years: Correspondence, 1902–1914. Princeton University Press, Princeton. External Links: Link Cited by: endnote 37, endnote 75.
- The Collected Papers of Albert Einstein, Volume 10, The Berlin Years: Correspondence, May–December 1920. Princeton University Press, Princeton. External Links: Link Cited by: endnote 18.
- The Scientific Correspondence of H. A. Lorentz, Volume 1. Springer, Berlin. Cited by: endnote 4, endnote 51, endnote 74.
- Sur l’origine des radiations et l’inertie électromagnétique. Journal de physique théorique et appliquée 4, pp. 165–183. External Links: Link Cited by: Figure 1, §4, §5.
- The relations of the physics of electrons to the other branches of science. See Congress of Arts and Science: Universal Exposition, St. Louis, 1904, Rogers, pp. 121–156. External Links: Link Cited by: §5.
- Æther and Matter. Cambridge University Press, Cambridge. External Links: Link Cited by: §4, endnote 9.
- Alfred Arthur Robb 1873–1936. Obituary Notices of Fellows of the Royal Society 2, pp. 315–321. Cited by: §7.
- Das Relativitätsprinzip. Vieweg, Braunschweig. Cited by: §8.
- Das Relativitätsprinzip. Jahrbücher der Philosophie 1, pp. 99–128. Cited by: §8.
- Geschichte der Physik. Universitäts-Verlag, Bonn. Cited by: §10.
- Mein physikalischer Werdegang; eine Selbstdarstellung. In Schöpfer des neuen Weltbildes: Große Physiker unserer Zeit, H. Hartmann (Ed.), pp. 178–207. Cited by: endnote 68.
- Die Relativitätstheorie: die spezielle Relativitätstheorie. Vieweg, Braunschweig. Cited by: endnote 72.
- Aufsätze und Vorträge. Vieweg, Braunschweig. Cited by: endnote 66.
- Über die Interferenzerscheinungen an planparallelen Platten. Ph.D. Thesis, University of Berlin, Berlin. Cited by: §8.
- Die Mitführung des Lichtes durch bewegte Körper nach dem Relativitätsprinzip. Annalen der Physik 328, pp. 989–990. Cited by: §8.
- Die Wellenstrahlung einer bewegten Punktladung nach dem Relativitätsprinzip. Berichte der Deutschen Physikalischen Gesellschaft 10, pp. 838–844. External Links: Link Cited by: §8.
- Das Relativitätsprinzip. Vieweg, Braunschweig. External Links: Link Cited by: §10, §2, Figure 12, §8.
- Zur Dynamik der Relativitätstheorie. Annalen der Physik 340, pp. 524–542. Cited by: endnote 67.
- Zwei Einwände gegen die Relativitätstheorie und ihre Widerlegung. Physikalische Zeitschrift 13, pp. 118–120. Cited by: §9.
- Sur un théorème de M. Einstein. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 155, pp. 1224–1227. Cited by: endnote 18.
- Vorlesungen über continuierliche Gruppen mit geometrischen und anderen Anwendungen. Teubner, Leipzig. External Links: Link Cited by: §3.
- Champ électrique et magnétique produit par une charge concentrée en un point et animée d’un mouvement quelconque. Éclairage électrique 16, pp. 5–14, 53–59, 106–112. External Links: Link Cited by: §4.
- Ueber den Einfluss magnetischer Kräfte auf die Emission des Lichtes. Annalen der Physik und Chemie 299, pp. 278–284. Cited by: §7.
- Electromagnetic phenomena in a system moving with any velocity less than that of light. Proceedings of the Section of Sciences, Koninklijke Akademie van Wetenschappen te Amsterdam 6, pp. 809–831. External Links: Link Cited by: §2, §2, §5.
- The Theory of Electrons and its Application to the Phenomena of Light and Radiant Heat. Columbia University Press, New York. External Links: Link Cited by: §5, §5, endnote 51.
- The Theory of Electrons and its Application to the Phenomena of Light and Radiant Heat. Teubner, Leipzig. Cited by: §5.
- On the identity of the vibrations of light with electrical currents. Philosophical Magazine 34 (230), pp. 287–301. Cited by: §4.
- The definition of rigidity in the special theory of relativity and the genesis of the general theory of relativity. Studies in History and Philosophy of Modern Physics 26 (3), pp. 263–306. Cited by: endnote 15.
- Universität, Technische Hochschule und Industrie. Duncker & Humblot, Berlin. Cited by: endnote 41.
- Kinematics: The Lost Origins of Einstein’s Relativity. Johns Hopkins University Press, Baltimore. Cited by: §2, endnote 2.
- Ebenezer Cunningham. Bulletin of the London Mathematical Society 10 (1), pp. 116–126. Cited by: endnote 6.
- A study of Henri Poincaré’s ‘Sur la dynamique de l’électron’. Archive for History of Exact Sciences 10 (3), pp. 207–328. External Links: Link, Document Cited by: endnote 20.
- On Einstein, light quanta, radiation and relativity in 1905. American Journal of Physics 44 (10), pp. 912–923. Cited by: endnote 42.
- Albert Einstein’s Special Theory of Relativity: Emergence (1905) and Early Interpretation. Addison-Wesley, Reading, MA. Cited by: §3, endnote 1.
- Die Grundgleichungen für die electromagnetischen Vorgänge in bewegten Körpern. Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, pp. 53–111. External Links: Link Cited by: §6, §6, §8, endnote 45, endnote 64.
- Raum und Zeit. Jahresbericht der deutschen Mathematiker-Vereinigung 18, pp. 75–88. External Links: Link Cited by: §2, §6, §8, §8, endnote 63.
- Das Relativitätsprinzip. Jahresbericht der deutschen Mathematiker-Vereinigung 24, pp. 372–382. Cited by: §6.
- Ueber die Principien der Galilei-Newton’schen Theorie. Teubner, Leipzig. External Links: Link Cited by: §2.
- The Lorentz transformation: simplification through complexification. American Journal of Physics 78 (1), pp. 14–19. Cited by: endnote 60.
- Einstein, Nordström and the early demise of Lorentz-covariant theories of gravitation. Archive for History of Exact Sciences 45, pp. 17–94. Cited by: endnote 70.
- Science in Germany. History of Science Society, Philadelphia. Cited by: D. E. Rowe (1989).
- Le principe de la relativité et les théories d’Einstein. Doin, Paris. External Links: Link Cited by: endnote 36.
- The apparent shape of a relativistically moving sphere. Proceedings of the Cambridge Philosophical Society 55, pp. 137–139. Cited by: endnote 53.
- Minkowski Spacetime: A Hundred Years Later. Springer, Berlin. External Links: Link, Document Cited by: S. A. Walter (2010).
- Zur Dynamik bewegter Systeme. Sitzungsberichte der königliche preußischen Akademie der Wissenschaften, pp. 542–570. Cited by: §6.
- Acht Vorlesungen über theoretische Physik. Hirzel, Leipzig. External Links: Link Cited by: Figure 11, §8.
- Sur la théorie des oscillations hertziennes. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 113, pp. 515–519. External Links: Link Cited by: §4.
- Électricité et optique: la lumière et les théories électrodynamiques. Carré et Naud, Paris. External Links: Link Cited by: endnote 26.
- L’état actuel et l’avenir de la physique mathématique. Bulletin des sciences mathématiques 28, pp. 302–324. External Links: Link Cited by: endnote 26.
- Science and Hypothesis. Walter Scott, London. External Links: Link Cited by: endnote 54.
- Sur la dynamique de l’électron. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 140, pp. 1504–1508. External Links: Link Cited by: §3.
- Sur la dynamique de l’électron. Rendiconti del Circolo matematico di Palermo 21, pp. 129–176. External Links: Link, Document Cited by: §3, §3, §5, §5.
- La relativité de l’espace. Année psychologique 13, pp. 1–17. External Links: Link Cited by: §5.
- La dynamique de l’électron. Revue générale des sciences pures et appliquées 19, pp. 386–402. External Links: Link Cited by: §5, §5, §5, endnote 17.
- Science et méthode. Flammarion, Paris. External Links: Link Cited by: endnote 17, endnote 34.
- La mécanique nouvelle. Revue scientifique 47-2 (6), pp. 170–177. External Links: Link Cited by: §5, endnote 17.
- La dynamique de l’électron. Dumas, Paris. External Links: Link Cited by: endnote 17, endnote 48.
- Physics in the shadow of mathematics: the Göttingen electron-theory seminar of 1905. Archive for History of Exact Sciences 21 (1), pp. 55–89. External Links: Link Cited by: §6, §8.
- The Genesis of General Relativity, Volume 3: Theories of Gravitation in the Twilight of Classical Physics, Between Mechanics, Field Theory, and Astronomy. Springer, Berlin. External Links: Link, Document Cited by: S. A. Walter (2007a).
- The Genesis of General Relativity. Springer, Berlin. External Links: Link, Document Cited by: J. Renn (2007b).
- The third way to general relativity. See The Genesis of General Relativity, Renn, Boston Studies in the Philosophy of Science, Vol. 250, pp. 21–75. External Links: Link, Document Cited by: endnote 42.
- Hyperbolic geometry on a hyperboloid. American Mathematical Monthly 100, pp. 442–455. Cited by: endnote 44.
- Sur la déformation des surfaces. Comptes rendus hebdomadaires des séances de l’Académie des sciences de Paris 70, pp. 330–333. Cited by: §8.
- Beiträge zur Theorie des Zeemaneffektes. Ph.D. Thesis, Georg-Augusta Universität Göttingen, Leipzig. Cited by: §7.
- Optical Geometry of Motion: A New View of the Theory of Relativity. W. Heffer and Sons, Cambridge. External Links: Link Cited by: Figure 10, §7, §7, endnote 54.
- Congress of Arts and Science: Universal Exposition, St. Louis, 1904. Houghton, Mifflin, Boston/New York. External Links: Link Cited by: P. Langevin (1906).
- Classical Charged Particles. World Scientific, Singapore. Cited by: endnote 11.
- Introductory Relativity. Butterworth, London. External Links: Link Cited by: endnote 71.
- Klein, Hilbert, and the Göttingen mathematical tradition. See Science in Germany, Olesko, Osiris, Vol. 5, pp. 186–213. Cited by: endnote 41.
- The Göttingen response to general relativity and Emmy Noether’s theorems. See The Symbolic Universe: Geometry and Physics, 1890–1930, Gray, pp. 189–233. Cited by: endnote 73.
- Max von Laue’s role in the relativity revolution. Mathematical Intelligencer 30 (3), pp. 54–60. Cited by: endnote 70.
- A look back at Hermann Minkowski’s Cologne lecture ‘Raum und Zeit’. Mathematical Intelligencer 31 (2), pp. 27–39. Cited by: endnote 47.
- The reception of special relativity in Great Britain. See The Comparative Reception of Relativity, Glick, pp. 27–58. Cited by: endnote 7.
- Mathematics Meets Physics: A Contribution to Their Interaction in the 19th and the First Half of the 20th Century. Harri Deutsch, Frankfurt am Main. Cited by: S. A. Walter (2011).
- On the steady motion of an electrified ellipsoid. Philosophical Magazine 44, pp. 329–341. External Links: Link Cited by: §4.
- Albert Einstein: Leben und Werk eines Genies unserer Zeit. Europa Verlag, Zurich. Cited by: §6.
- The Theory of Relativity. Macmillan, London. External Links: Link Cited by: §7, §7.
- Anmerkungen zu Minkowski, Raum und Zeit. See Das Relativitätsprinzip; Eine Sammlung von Abhandlungen, Blumenthal, pp. 69–73. External Links: Link Cited by: §6.
- Atombau und Spektrallinien. Vieweg, Braunschweig. Cited by: §2.
- Vorlesungen über theoretische Physik, Bd. 3: Elektrodynamik. Dieterich, Wiesbaden. Cited by: endnote 16.
- The Collected Papers of Albert Einstein, Volume 2, The Swiss Years: Writings, 1900–1909. Princeton University Press, Princeton. External Links: Link Cited by: endnote 14.
- On the histories of relativity: the propagation and elaboration of relativity theory in participant histories in Germany, 1905–1911. Isis 89 (2), pp. 263–299. External Links: Link Cited by: §1, endnote 70.
- Imagery in Scientific Thought by Arthur I. Miller. Mathematical Intelligencer 8 (2), pp. 65–74. Cited by: §5.
- The Historical Register of the University of Cambridge, Being a Supplement to the Calendar with a Record of University Offices, Honours and Distinctions to the Year 1910. Cambridge University Press, Cambridge. External Links: Link Cited by: endnote 49.
- Notes on Recent Researches in Electricity and Magnetism: Intended as a Sequel to Professor Clerk-Maxwell’s Treatise on Electricity and Magnetism. Clarendon, Oxford. External Links: Link Cited by: §4.
- Über ein einfaches geometrisches Bild der Raumzeitwelt Minkowskis. Jahresbericht der deutschen Mathematiker-Vereinigung 21, pp. 274–285. External Links: Link Cited by: §8.
- Über die Raumzeitvektoren und ihre geometrische Behandlung. In Festschrift Julius Elster und Hans Geistel zum sechzigsten Geburtstage: Arbeiten aus den Gebieten der Physik, Mathematik, Chemie, K. Bergwitz (Ed.), pp. 514–520. Cited by: §8.
- The second postulate of relativity. Physical Review 31, pp. 26–40. Cited by: §2.
- The principle of similitude. Physical Review 3, pp. 244–255. External Links: Link Cited by: endnote 24.
- Relativity and Geometry. Dover Publications, New York. Cited by: endnote 76.
- Comptes rendus du Congrès international des mathématiciens : Strasbourg, 22–30 septembre 1920. Edouard Privat, Toulouse. Cited by: É. Guillaume (1921).
- Minkowski, mathematicians, and the mathematical theory of relativity. See The Expanding Worlds of General Relativity, Goenner et al., Einstein Studies, Vol. 7, pp. 45–86. External Links: Link Cited by: §1, §1, §6, endnote 40, endnote 46.
- The non-Euclidean style of Minkowskian relativity. See The Symbolic Universe: Geometry and Physics, 1890–1930, Gray, pp. 91–127. External Links: Link Cited by: endnote 52.
- Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910. See The Genesis of General Relativity, Volume 3: Theories of Gravitation in the Twilight of Classical Physics, Between Mechanics, Field Theory, and Astronomy, Renn and Schemmel, pp. 193–252. External Links: Link, Document Cited by: §6.
- La correspondance d’Henri Poincaré, Volume 2: La correspondance entre Henri Poincaré et les physiciens, chimistes et ingénieurs. Birkhäuser, Basel. External Links: Link, Document Cited by: endnote 2.
- Hermann Minkowski’s approach to physics. Mathematische Semesterberichte 55 (2), pp. 213–235. External Links: Link, Document Cited by: endnote 40.
- Hypothesis and convention in Poincaré’s defense of Galilei spacetime. See The Significance of the Hypothetical in the Natural Sciences, Heidelberger and Schiemann, pp. 193–219. External Links: Link, Document Cited by: §6, endnote 2, endnote 25.
- Minkowski’s modern world. See Minkowski Spacetime: A Hundred Years Later, Petkov, Fundamental Theories of Physics, Vol. 165, pp. 43–61. External Links: Link, Document Cited by: §6, §9.
- Henri Poincaré, theoretical physics and relativity theory in Paris. See Mathematics Meets Physics: A Contribution to Their Interaction in the 19th and the First Half of the 20th Century, Schlote and Schneider, pp. 213–239. External Links: Link Cited by: endnote 35.
- Poincaré on clocks in motion. Studies in History and Philosophy of Modern Physics 47 (1), pp. 131–141. External Links: Link, Document Cited by: §5, §5, endnote 32.
- Henri Poincaré Papers. http://henripoincarepapers.univ-nantes.fr, Nantes. External Links: Link Cited by: §5.
- Henri Poincaré’s life, science, and life in science. Historia Mathematica 44 (4), pp. 425–435. External Links: Link, Document Cited by: endnote 31.
- Poincaré-week in Göttingen, in light of the Hilbert-Poincaré correspondence of 1908–1909. See Mathematical Correspondences and Critical Editions, Borgato et al., pp. 297–310. External Links: Link, Document Cited by: endnote 30.
- Masters of Theory: Cambridge and the Rise of Mathematical Physics. University of Chicago, Chicago. Cited by: endnote 64, endnote 65, endnote 7.
- Das Raumproblem. Jahresbericht der deutschen Mathematiker-Vereinigung 31, pp. 205–221. Cited by: §7.
- A History of the Theories of Aether and Electricity, Volume 2: The Modern Theories, 1900–1926. T. Nelson, London. External Links: Link Cited by: endnote 64.
- Elektrodynamische Elementargesetze. In Recueil de travaux offerts par les auteurs à H. A. Lorentz, J. Bosscha (Ed.), Archives néerlandaises des sciences exactes et naturelles, Vol. 5, pp. 549–573. Cited by: §4.
- Relativitätsprinzip und Äther. Physikalische Zeitschrift 12, pp. 689–707, 737–758. Cited by: §8, §9, §9, endnote 74.
- Logical economy in Einstein’s ‘On the electrodynamics of moving bodies’. Studies in History and Philosophy of Science 8 (1), pp. 46–60. Cited by: endnote 3.
- Henri Poincaré: A Developmental Study of His Philosophical and Scientific Thought. Ph.D. Thesis, Harvard University, Cambridge MA. Cited by: §5.
- Poincaré’s philosophy of geometry, or does geometric conventionalism deserve its name?. Studies in History and Philosophy of Modern Physics 28, pp. 183–218. Cited by: endnote 39.