The historical origins of spacetime
Published in A. Ashtekar and V. Petkov (eds)
The Springer Handbook of Spacetime
Springer: Berlin, 2014, chapter 2, 27–38
Introduction
The idea of spacetime investigated in this chapter, with a view toward understanding its immediate sources and development, is the one formulated and proposed by Hermann Minkowski in 1908. Until recently, the principle source used to form historical narratives of Minkowski’s discovery of spacetime has been Minkowski’s own discovery account, outlined in the lecture he delivered in Cologne, entitled “Space and time” [27]. Minkowski’s lecture is usually considered as a bona fide first-person narrative of lived events. According to this received view, spacetime was a natural outgrowth of Felix Klein’s successful project to promote the study of geometries via their characteristic groups of transformations. Or as Minkowski expressed the same basic thought himself, the theory of relativity discovered by the physicists in 1905 could just as well have been proposed by some late-nineteenth-century mathematician, by simply reflecting upon the groups of transformations that left invariant the form of the equation of a propagating light wave.
Minkowski’s publications and research notes provide a contrasting picture of the discovery of spacetime, in which group theory plays no direct part. In order to relate the steps of Minkowski’s discovery, I begin with an account of Poincaré’s theory of gravitation, where Minkowski found some of the germs of spacetime. Poincaré’s geometric interpretation of the Lorentz transformation is examined, along with his reasons for not pursuing a four-dimensional vector calculus. In the second section, Minkowski’s discovery and presentation of the notion of a worldline in spacetime is presented. In the third and final section, Poincaré’s and Minkowski’s diagrammatic interpretations of the Lorentz transformation are compared.
2.1 Poincaré’s theory of gravitation
In the month of May, 1905, Henri Poincaré (1854–1912) wrote to his Dutch colleague H. A. Lorentz (1853–1928) to apologize for missing the latter’s lecture in Paris, and also to communicate his latest discovery, which was related to Lorentz’s recent paper [22] on electromagnetic phenomena in frames moving with sublight velocity [49, §38.3]. In [22], Lorentz had shown that the form of the fundamental equations of his theory of electrons is invariant with respect to the coordinate transformations:
| (2.1) | ||||
where
The latter transformation was understood to compose with a transformation later known as a “Galilei” transformation: , . (Both here and elsewhere in this chapter, original notation is modified for ease of reading.)
The essence of Poincaré’s discovery in May 1905, communicated in subsequent letters to Lorentz, was that the coordinate transformations employed by Lorentz form a group, provided that the factor is set to unity. Poincaré performed the composition of the two transformations to obtain a single transformation, which he called the “Lorentz” transformation:
| (2.2) | ||||
In his letters to Lorentz, Poincaré noted that while he had concocted an electron model that was both stable and relativistic, in the new theory he was unable to preserve the “unity of time”, i.e., a definition of duration valid in both the ether and in moving frames.
The details of Poincaré’s theory [31] were published in January, 1906, by which time Einstein had published his own theory of relativity [8], which employed the “unified” form of the Lorentz transformation (2.2), and vigorously embraced the relativity of space and time with respect to inertial frames of motion. The final section of Poincaré’s memoir is devoted to a topic he had neglected to broach with Lorentz, and that Einstein had neglected altogether: gravitation.
If the principle of relativity was to be universally valid, Poincaré reasoned, then Newton’s law of gravitation would have to be modified. An adept of the group-theoretical understanding of geometry since his discovery of what he called “Fuchsian” functions in 1880 [14], Poincaré realized that a Lorentz transformation may be construed as a rotation about the origin of coordinates in a four-dimensional vector space with three real axes and one imaginary axis, preserving the sum of squares:
| (2.3) |
where Poincaré set . Employing the substitution , and drawing on a method promoted by Sophus Lie and Georg Scheffers in the early 1890s [21], Poincaré identified a series of quantities that are invariant with respect to the Lorentz Group. These quantities were meant to be the fundamental building blocks of a Lorentz-covariant family of laws of gravitational attraction. Neglecting a possible dependence on acceleration, and assuming that the propagation velocity of gravitation is the same as that of light in empty space, Poincaré identified a pair of laws, one vaguely Newtonian, the other vaguely Maxwellian, that he expressed in the form of what would later be called four-vectors.
In the course of his work on Lorentz-covariant gravitation, Poincaré defined several quadruples formally equivalent to four-vectors, including definitions of radius, velocity, force, and force density. The signs of Poincaré’s invariants suggest that when he formed them, he did not consider them to be scalar products of four-vectors. This state of affairs led at least one contemporary observer to conclude – in the wake of Minkowski’s contributions – that Poincaré had simply miscalculated one of his Lorentz invariants [48, 203, 238].
Poincaré’s four-dimensional vector space attracted little attention at first, except from the vectorist Roberto Marcolongo (1862–1945), Professor of Mathematical Physics in Messina. Redefining Poincaré’s temporal coordinate as , Marcolongo introduced four-vector definitions of current and potential, which enabled him to express the Lorentz-covariance of the equations of electrodynamics in matricial form [23]. Largely ignored at the time, Marcolongo’s paper nonetheless broke new ground in applying Poincaré’s four-dimensional approach to the laws of electrodynamics.
Marcolongo was one of many ardent vectorists active in the first decade of the twentieth century, when vector methods effectively sidelined the rival quaternionic approaches [5, 259]. More and more theorists recognized the advantages of vector analysis, and also of a unified vector notation for mathematical physics. The pages of the leading journal of theoretical physics, the Annalen der Physik, edited by Paul Drude until his suicide in 1906, then by Max Planck and Willy Wien, bear witness to this evolution. Even in the pages of the Annalen der Physik, however, notation was far from standardized, leading several theorists to deplore the field’s babel of symbolic expressions.
Among the theorists who regretted the multiplication of systems of notation was Poincaré, who employed ordinary vectors in his own teaching and publications on electrodynamics, while ignoring the notational innovations of Lorentz and others. In particular, Poincaré saw no future for a four-dimensional vector calculus. Expressing physical laws by means of such a calculus, he wrote in 1907, would entail “much trouble for little profit” [13, 438].
This was not a dogmatic view, and in fact, some years later he acknowledged the value of a four-dimensional approach in theoretical physics [51, 210]. He was already convinced that there was a place for -dimensional geometries at the university. As Poincaré observed in the paper Gaston Darboux read in his stead at the International Congress of Mathematicians in Rome, in April, 1908, university students were no longer taken aback by geometries with “more than three dimensions” [32, 938].
Relativity theory, however, was another matter for Poincaré. Recently-rediscovered manuscript notes by Henri Vergne of Poincaré’s lectures on relativity theory in 1906–1907 reveal that Poincaré introduced his students to the Lorentz Group, and taught them how to form Lorentz-invariant quantities with real coordinates. He also taught his students that the sum of squares (2.3) is invariant with respect to the transformations of the Lorentz Group. Curiously, Poincaré did not teach his students that a Lorentz transformation corresponded to a rotation about the origin in a four-dimensional vector space with one imaginary coordinate. He also neglected to show students the handful of four-vectors he had defined in the summer of 1905. Apparently for Poincaré, knowledge of the Lorentz Group and the formation of Lorentz-invariant quantities was all that was needed for the physics of relativity. In other words, Poincaré acted as if one could do without an interpretation of the Lorentz transformation in four-dimensional geometry.
If four-dimensional geometry was superfluous to interpretation of the Lorentz transformation, the same was not true for plane geometry. Evidence of this view is found in Vergne’s notes, which feature a curious figure that I’ll call a light ellipse, redrawn here as Figure 2.1. Poincaré’s light ellipse is given to be the meridional section of an ellipsoid of rotation representing the locus of a spherical light pulse at an instant of time. It works as follows: an observer at rest with respect to the ether measures the radius of a spherical light pulse at an instant of absolute time (as determined by clocks at rest with respect to the ether). The observer measures the light pulse radius with measuring rods in uniform motion of velocity . These flying rods are Lorentz-contracted, while the light wave is assumed to propagate spherically in the ether. Consequently, for Poincaré, the form of a spherical light pulse measured in this fashion is that of an ellipsoid of rotation, elongated in the direction of motion of the flying rods. (A derivation of the equation of Poincaré’s light ellipse is provided along these lines in [6].)
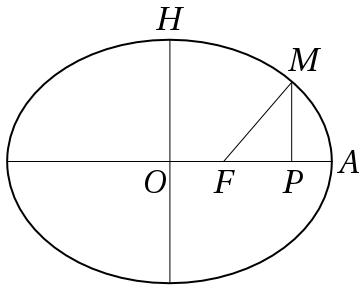
The light ellipse originally concerned ether-fixed observers measuring a locus of light with clocks at absolute rest, and rods in motion. Notably, in his first discussion of the light ellipse, Poincaré neglected to consider the point of view of observers in motion with respect to the ether. In particular, Poincaré’s graphical model of light propagation does not display relativity of simultaneity for inertial observers, since it represents a single frame of motion. Nonetheless, Poincaré’s light ellipse was applicable to the case of observers in uniform motion, as he showed himself in 1909. In this case, the radius vector of the light ellipse represents the light-pulse radius at an instant of “apparent” time , as determined by comoving, light-synchronized clocks, and comoving rods corrected for Lorentz-contraction. Such an interpretation implies that clock rates depend on frame velocity, as Einstein recognized in 1905 in consequence of his kinematic assumptions about ideal rods and clocks [8, 904], and which Poincaré acknowledged in a lecture in Göttingen on 28 April, 1909, as an effect epistemically akin to Lorentz-contraction, induced by clock motion with respect to the ether [34, 55].
Beginning in August 1909, Poincaré repurposed his light ellipse diagram to account for the apparent dilation of periods of ideal clocks in motion with respect to the ether [33, 174]. This sequence of events raises the question of what led Poincaré to embrace the notion of time deformation in moving frames, and to repurpose his light ellipse? He didn’t say, but there is a plausible explanation at hand, that I will return to later, as it rests on events in the history of relativity from 1907 to 1908 to be discussed in the next section.
2.2 Minkowski’s path to spacetime
From the summer of 1905 to the fall of 1908, the theory of relativity was reputed to be inconsistent with the observed deflection of -rays by electric and magnetic fields. In view of experimental results published by Walter Kaufmann (1871–1947), Lorentz wrote in despair to Poincaré on 8 March 1906 in hopes that the Frenchman would find a way to save his theory. As far as Lorentz was concerned, he was “at the end of [his] Latin” [24, 334].
Apparently, Poincaré saw no way around Kaufmann’s results, either. But by the end of 1908, the outlook for relativity theory had changed for the better, thanks in part to new experiments performed by A. H. Bucherer (1863–1927), which tended to confirm the predictions of relativity theory. The outlook for the latter theory was also enhanced by the contributions of a mathematician in Göttingen, Hermann Minkowski (1864–1909).
Minkowski’s path to theoretical physics was a meandering one, that began in earnest during his student days in Berlin, where he heard lectures by Hermann Helmholtz, Gustav Kirchhoff, Carl Runge, and Woldemar Voigt. There followed a dissertation in Königsberg on quadratic forms, and Habilitation in Bonn on a related topic in 1887 [40]. While in Bonn, Minkowski frequented Heinrich Hertz’s laboratory beginning in December, 1890, when it was teeming with young physicists eager to master techniques for the study of electromagnetic wave phenomena. Minkowski left Bonn for a position at the University of Königsberg, where he taught mathematics until 1896, and then moved to Switzerland, where he joined his former teacher Adolf Hurwitz (1859–1919) on the faculty of Zürich Polytechnic. In Zürich he taught courses in mathematics and mathematical physics to undergraduates including Walther Ritz (1878–1909), Marcel Grossmann (1878–1936), and Albert Einstein (1879–1955). In 1902, Minkowski accepted the offer to take up a new chair in mathematics created for him in Göttingen at the request of his good friend, David Hilbert (1862–1943) [38, 436].
Minkowski’s arrival in Göttingen comforted the university’s premier position in mathematical research in Germany. His mathematical credentials were well-established following the publication, in 1896, of the seminal Geometry of Numbers [25]. During his first two years in Göttingen, Minkowski continued to publish in number theory, and to teach pure mathematics. With Hilbert, who had taken an interest in questions of mathematical physics in the 1890s, Minkowski co-directed a pair of seminars on stability and mechanics [4].
It was quite unusual at the time for Continental mathematicians to pursue research in theoretical physics. Arguably, Poincaré was the exception that proved the rule, in that no other scientist displayed comparable mastery of research in both mathematics and theoretical physics. In Germany, apart from Carl Neumann, mathematicians left physics to the physicists. With the construction in Germany of twelve new physical institutes between 1870 and 1899, there emerged a professional niche for individuals trained in both mathematical physics and experimental physics, that very few mathematicians chose to enter. This “institutional revolution” in German physics [3] gave rise to a new breed of physicist: the “theoretical” physicist [18, 19].
In the summer of 1905, Minkowski and Hilbert co-directed a third seminar in mathematical physics, convinced that only higher mathematics could solve the problems then facing physicists, and with Poincaré’s fourteen volumes of Sorbonne lectures on mathematical physics serving as an example. This time they delved into a branch of physics new to both of them: electron theory. Their seminar was an occasion for them to acquaint themselves, their colleagues Emil Wiechert and Gustav Herglotz, and students including Max Laue and Max Born, with recent research in electron theory. From all accounts, the seminar succeeded in familiarizing its participants with the state of the art in electron theory, although the syllabus did not feature the most recent contributions from Lorentz and Poincaré [35]. In particular, according to Born’s distant recollections of the seminar, Minkowski “occasionally hinted” of his engagement with the Lorentz transformation, and he conveyed an “inkling” of the results he would publish in 1908 [50].
The immediate consequence of the electron-theory seminar for Minkowski was a new interest in a related, and quite-puzzling topic in theoretical physics: blackbody radiation. Minkowski gave two lectures on heat radiation in 1906, and offered a lecture course in this subject during the summer semester of 1907. According to Minkowski’s class notes, he referred to Max Planck’s contribution to the foundations of relativistic thermodynamics [30], which praised Einstein’s formulation of a general approach to the principle of relativity for ponderable systems. In fact, Minkowski had little time to assimilate Planck’s findings (communicated on 13 June 1907) and communicate them to his students. This may explain why his lecture notes cover only non-relativistic approaches to heat radiation.
By the fall of 1907, Minkowski had come to realize some important consequences of relativity theory not only for thermodynamics, but for all of physics. On 9 October, he wrote to Einstein, requesting an offprint of his first paper on relativity, which was the one cited by Planck [20, Doc. 62]. Less than a month later, on 5 November 1907, Minkowski delivered a lecture to the Göttingen Mathematical Society, the subject of which was described succinctly as “On the principle of relativity in electrodynamics: a new form of the equations of electrodynamics” [50].
The lecture before the mathematical society was the occasion for Minkowski to unveil a new research program: to reformulate the laws of physics in four-dimensional terms, based on the Lorentz-invariance of the quadratic form , where , , , are rectangular space coordinates, fixed “in ether,” is time, and is the vacuum speed of light [28, 374]. Progress toward the achievement of such a reformulation had been realized by Poincaré’s relativistic reformulation of the law of gravitation in terms of Lorentz-invariant quantities expressed in the form of four-vectors, as mentioned above.
Poincaré’s formal contribution was duly acknowledged by Minkowski, who intended to go beyond what the Frenchman had accomplished in 1905. He also intended to go beyond what Poincaré had considered to be desirable, with respect to the application of geometric reasoning in the physical sciences. Poincaré, we recall, had famously predicted that Euclidean geometry would forever remain the most convenient one for physics [13, 45]. Poincaré’s prediction stemmed in part from his doctrine of physical space, according to which the question of the geometry of phenomenal space cannot be decided on empirical grounds. In fact, few of Poincaré’s contemporaries in the physical and mathematical sciences agreed with his doctrine [45].
Euclidean geometry was to be discarded in favor of a certain four-dimensional manifold, and not just any manifold, but a non-Euclidean manifold. The reason for this was metaphysical, in that for Minkowski, the phenomenal world was not Euclidean, but non-Euclidean and four-dimensional:
The world in space and time is, in a certain sense, a four-dimensional non-Euclidean manifold. [28, 372]
Explaining this enigmatic proposition would take up the rest of Minkowski’s lecture.
To begin with, Minkowski discussed neither space, time, manifolds, or non-Euclidean geometry, but vectors. Borrowing Poincaré’s definitions of radius and force density, and adding (like Marcolongo before him) expressions for four-current density, , and four-potential, , Minkowski expressed Maxwell’s vacuum equations in the compact form:
| (2.4) |
where is the Dalembertian operator. According to Minkowski, no one had realized before that the equations of electrodynamics could be written so succinctly, “not even Poincaré” (cf. [11]). Apparently, Minkowski had not noticed Marcolongo’s paper, mentioned above.
The next mathematical object that Minkowski introduced was a real step forward, and soon acknowledged as such by physicists. This is what Minkowski called a “Traktor”: a six-component object later called a “six-vector”, and more recently, an antisymmetric rank-2 tensor. Minkowski defined the Traktor’s six components via his four-vector potential, using a two-index notation: , noting the antisymmetry relation , and zeros along the diagonal , such that the components , , , , , match the field quantities , , , , , . To express the source equations, Minkowski introduced a “Polarisationstraktor”, :
| (2.5) |
where is the four-current density for matter.
Up to this point in his lecture, Minkowski had presented a new and valuable mathematical object, the antisymmetric rank-2 tensor. He had yet to reveal the sense in which the world is a “four-dimensional non-Euclidean manifold”. His argument proceeded as follows. The tip of a four-dimensional velocity vector , , , , Minkowski explained,
is always a point on the surface
(2.6) or if you prefer, on
(2.7) and represents both the four-dimensional vector from the origin to this point, and null velocity, or rest, being a genuine vector of this sort. Non-Euclidean geometry, of which I spoke earlier in an imprecise fashion, now unfolds for these velocity vectors. [28, 373]
These two surfaces, a pseudo-hypersphere of unit imaginary radius (2.6), and its real counterpart, the two-sheeted unit hyperboloid (2.7), give rise to well-known models of hyperbolic space, popularized by Helmholtz in the late nineteenth century [17, Vol. 2]. The upper sheet () of the unit hyperboloid (2.7) models hyperbolic geometry; for details, see [37].
The conjugate diameters of the hyperboloid (2.7) give rise to a geometric image of the Lorentz transformation. Any point on (2.7) can be considered to be at rest, i.e., it may be taken to lie on a -diameter, as shown in Figure 2.2. This change of axes corresponds to an orthogonal transformation of the time and space coordinates, which is a Lorentz transformation (letting ). In other words, the three-dimensional hyperboloid (2.7) embedded in four-dimensional pseudo-Euclidean space affords an interpretation of the Lorentz transformation.
Although Minkowski did not spell out his geometric interpretation, he probably recognized that a displacement on the hypersurface (2.7) corresponds to a rotation about the origin, such that frame velocity is described by a hyperbolic function, . However, he did not yet realize that his hypersurfaces represent the set of events occurring at coordinate time of all inertial observers, the worldlines of whom pass through the origin of coordinates (with a common origin of time). According to (2.7), this time is imaginary, a fact which may have obscured the latter interpretation.
How do we know that Minkowski was still unaware of worldlines in spacetime? Inspection of Minkowski’s definition of four-velocity vectors reveals an error, which is both trivial and interesting: trivial from a mathematical standpoint, and interesting for what it says about his knowledge of the structure of spacetime, and the progress he had realized toward his goal of replacing the Euclidean geometry of phenomenal space with the geometry of a four-dimensional non-Euclidean manifold.
When faced with the question of how to define a four-velocity vector, Minkowski had the option of adopting the definition given by Poincaré in 1905. Instead, he rederived his own version, by following a simple rule. Minkowski defined a four-vector potential, four-current density, and four-force density, all by simply generalizing ordinary three-component vectors to their four-component counterparts. When he came to define four-velocity, he took over the components of the ordinary velocity vector for the spatial part of four-velocity, and added an imaginary fourth component, . This resulted in four components of four-velocity, , , , :
| (2.8) |
Since the components of Minkowski’s quadruplet do not transform like the coordinates of his vector space , , , , they lack what he knew to be a four-vector property.
Minkowski’s error in defining four-velocity indicates that he did not yet grasp the notion of four-velocity as a four-vector tangent to the worldline of a particle [48]. If we grant ourselves the latter notion, then we can let the square of the differential parameter of a given worldline be , such that the 4-velocity may be defined as the first derivative with respect to , (, 2, 3, 4). In addition to a valid four-velocity vector, Minkowski was missing a four-force vector, and a notion of proper time. In light of these significant lacunæ in his knowledge of the basic mathematical objects of four-dimensional physics, Minkowski’s triumphant description of his four-dimensional formalism as “virtually the greatest triumph ever shown by the application of mathematics” [28, 373] is all the more remarkable, and bears witness to the depth of Minkowski’s conviction that he was on the right track.
Sometime after Minkowski spoke to the Göttingen Mathematical Society, he repaired his definition of four-velocity, and perhaps in connection with this, he came up with the constitutive elements of his theory of spacetime. In particular, he formulated the idea of proper time as the parameter of a hyperline in spacetime, the light-hypercone structure of spacetime, and the spacetime equations of motion of a material particle. He expressed his new theory in a sixty-page memoir [26] published in the Göttinger Nachrichten on 5 April, 1908.
His memoir, entitled “The basic equations for electromagnetic processes in moving bodies” made for challenging reading. It was packed with new notation, terminology, and calculation rules, it made scant reference to the scientific literature, and offered no figures or diagrams. Minkowski defined a single differential operator, named lor in honor of Lorentz, which streamlined his expressions, while rendering them all the more unfamiliar to physicists used to the three-dimensional operators of ordinary vector analysis.
Along the same lines, Minkowski rewrote velocity, denoted , in terms of the tangent of an imaginary angle ,
| (2.9) |
where . From his earlier geometric interpretation of hyperbolic velocity space, Minkowski kept the idea that every rotation of a -diameter corresponds to a Lorentz transformation, which he now expressed in terms of :
| (2.10) | |||||
Minkowski was undoubtedly aware of the connection between the composition of Lorentz transformations and velocity composition, but he did not mention it. In fact, Minkowski neither mentioned Einstein’s law of velocity addition, nor expressed it mathematically.
While Minkowski made no appeal in “The basic equations” to the hyperbolic geometry of velocity vectors, he retained the hypersurface (2.7) on which it was based, and provided a new interpretation of its physical significance. This interpretation represents an important clue to understanding how Minkowski discovered the worldline structure of spacetime. The appendix to “The basic equations” rehearses the argument according to which one may choose any point on (2.7) such that the line from this point to the origin forms a new time axis, and corresponds to a Lorentz transformation. He further defined a “spacetime line” to be the totality of spacetime points corresponding to any particular point of matter for all time .
With respect to the new concept of a spacetime line, Minkowski noted that its direction is determined at every spacetime point. Here Minkowski introduced the notion of “proper time” (Eigenzeit), , expressing the increase of coordinate time for a point of matter with respect to :
| (2.11) |
where is the square of ordinary velocity, , and , which silently corrects the flawed definition of this fourth component of four-velocity (2.8) delivered by Minkowski in his November 5 lecture.
Although Minkowski did not connect four-velocity to Einstein’s law of velocity addition, others did this for him, beginning with Sommerfeld, who expressed parallel velocity addition as the sum of tangents of an imaginary angle [41]. Minkowski’s former student Philipp Frank reexpressed both velocity and the Lorentz transformation as hyperbolic functions of a real angle [10]. The Serbian mathematician Vladimir Varičak found relativity theory to be ripe for application of hyperbolic geometry, and recapitulated several relativistic formulæ in terms of hyperbolic functions of a real angle [44]. A small group of mathematicians and physicists pursued this “non-Euclidean style” of Minkowskian relativity, including Varičak, Alfred Robb, Émile Borel, Gilbert Newton Lewis, and Edwin Bidwell Wilson [47].
The definition of four-velocity was formally linked by Minkowski to the hyperbolic space of velocity vectors in “The basic equations”, and thereby to the lightcone structure of spacetime. Some time before Minkowski came to study the Lorentz transformation in earnest, both Einstein and Poincaré understood light waves in empty space to be the only physical objects immune to Lorentz contraction. Minkowski noticed that when light rays are considered as worldlines, they divide spacetime into three regions, corresponding to the spacetime region inside a future-directed () hypercone (“Nachkegel”), the region inside a past-directed () hypercone (“Vorkegel”), and the region outside any such hypercone pair. The propagation in space and time of a spherical light wave is described by a hypercone, or what Minkowski called a lightcone (“Lichtkegel”).
One immediate consequence for Minkowski of the lightcone structure of spacetime concerned the relativity of simultaneity. In a section of “The basic equations” entitled “The concept of time”, Minkowski [26, § 6] showed that Einstein’s relativity of simultaneity is not absolute. While the relativity of simultaneity is indeed valid for two or three simultaneous “events” (Ereignisse), the simultaneity of four events is absolute, so long as the four spacetime points do not lie on the same spatial plane. Minkowski’s demonstration relied on the Einstein simultaneity convention, and employed both light signals and spacetime geometry. His result showed the advantage of employing his spacetime geometry in physics, and later writers – including Poincaré – appear to have agreed with him, by attributing to spacetime geometry the discovery of the existence of a class of events for a given observer that can be the cause of no other events for the same observer [51, 210].
Another signature result of Minkowski’s spacetime geometry was the geometric derivation of a Lorentz-covariant law of gravitation. Like Poincaré, Minkowski proposed two four-vector laws of gravitation, exploiting analogies to Newtonian gravitation and Maxwellian electrodynamics, respectively. Minkowski presented only the Newtonian version of the law of gravitation in “The basic equations”, relating the states of two massive particles in arbritrary motion, and obtaining an expression for the spacelike component of the four-force of gravitation. Although his derivation involved a new spacetime geometry, Minkowski did not illustrate graphically his new law, a decision which led some physicists to describe his theory as unintelligible. According to Minkowski, however, his achievement was a formal one, inasmuch as Poincaré had formulated his theory of gravitation by proceeding in what he described as a “completely different way” [48, 225].
Few were impressed at first by Minkowski’s innovations in spacetime geometry and four-dimensional vector calculus. Shortly after “The basic equations” appeared in print, two of Minkowski’s former students, Einstein and Laub, discovered what they believed to be an infelicity in Minkowski’s definition of ponderomotive force density [43]. These two young physicists were more impressed by Minkowski’s electrodynamics of moving media than by the novel four-dimensional formalism in which it was couched, which seemed far too laborious. Ostensibly as a service to the community, Einstein and Laub reexpressed Minkowski’s theory in terms of ordinary vector analysis [42, Doc. 51].
Minkowski’s reaction to the latter work is unknown, but it must have come to him as a disappointment. According to Max Born, Minkowski always aspired
…to find the form for the presentation of his thoughts that corresponded best to the subject matter. [2]
The form Minkowski gave to his theory of moving media in “The basic equations” had been judged unwieldy by a founder of relativity theory, and in the circumstances, decisive action was called for if his formalism was not to be ignored. In September 1908, during the annual meeting of the German Association of Scientists and Physicians in Cologne, Minkowski took action, by affirming the reality of the four-dimensional “world”, and its necessity for physics [52]. The next section focuses on the use to which Minkowski put spacetime diagrams in his Cologne lecture, and how these diagrams relate to Poincaré’s light ellipse.
2.3 Spacetime diagrams
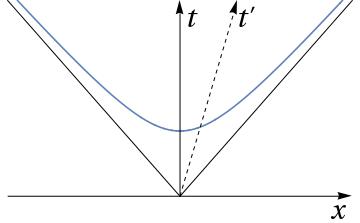
One way for Minkowski to persuade physicists of the value of his spacetime approach to understanding physical interactions was to appeal to their visual intuition [11]. From the standpoint of visual aids, the contrast between Minkowski’s two publications on spacetime is remarkable: where “The basic equations” is bereft of diagrams and illustrations, Minkowski’s Cologne lecture makes effective use of diagrams in two and three dimensions. For instance, Minkowski employed a two-dimensional spacetime diagrams to illustrate FitzGerald-Lorentz contraction of an electron, and the lightcone structure of spacetime (see Figure 2.3).

Minkowski’s lecture in Cologne, entitled “Space and time”, offered two diagrammatic readings of the Lorentz transformation, one of his own creation, the other he attributed to Lorentz and Einstein. One of these readings was supposed to represent the kinematics of the theory of relativity of Lorentz and Einstein. In fact, Minkowski’s reading captured Lorentzian kinematics, but distorted those of Einstein, and prompted corrective action from Philipp Frank, Guido Castelnuovo, and Max Born [46]. The idea stressed by Minkowski was that in the (Galilean) kinematics employed in Lorentz’s electron theory, time being absolute, the temporal axis on a space-time diagram may be rotated freely about the coordinate origin in the upper half-plane (), as shown in Figure 2.4. The location of a point may be described with respect to frames and , corresponding to axes and , respectively, according to the transformation: , .
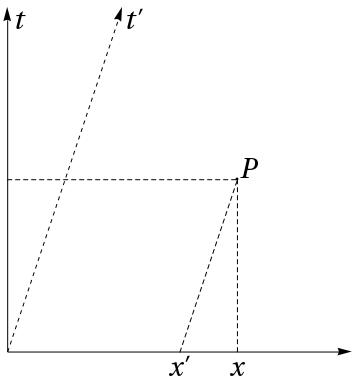
In contradistinction to the latter view, the theory proposed by Minkowski required a certain symmetry between the spatial and temporal axes. This constraint on symmetry sufficed for a geometric derivation of the Lorentz transformation. Minkowski described his spacetime diagram (Figure 2.5) as an illustration of the Lorentz transformation, and provided an idea of a demonstration in “Space and time”. A demonstration was later supplied by Sommerfeld, in an editorial note to his friend’s lecture [1], which appeared in an anthology of papers on the theory of relativity edited by Otto Blumenthal [39, 37].
Minkowski’s spacetime map was not the only illustration of relativistic kinematics available to scientists in the first decade of the twentieth century. Theorists pursuing the non-Euclidean style of Minkowskian relativity had recourse to models of hyperbolic geometry on occasion. The Poincaré half-plane and disk models of hyperbolic geometry were favored by Varičak in this context, for example. Poincaré himself did not employ such models in his investigations of the principle of relativity, preferring his light ellipse.
Of these three types of diagram, the light ellipse, spacetime map, and hyperbolic map, only the spacetime map attracted a significant scientific following. The relation between the spacetime map and the hyperbolic maps was underlined by Minkowski, as shown above in relation to surfaces (2.6) and (2.7). There is also a relation between the light ellipse and the spacetime map, although this may not have been apparent to either Poincaré or Minkowski. Their published appreciations of each other’s contributions to relativity field the barest of acknowledgments, suggesting no substantial intellectual indebtedness on either side.
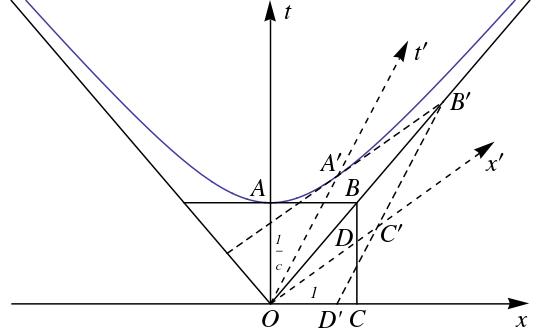
The diagrams employed in the field of relativity by Poincaré and Minkowski differ in several respects, but one difference in particular stands out. On the one hand, the light ellipse represents spatial relations in a plane defined as a meridional section of an ellipsoid of rotation. A Minkowski diagram, on the other hand, involves a temporal axis in addition to a spatial axis (or two, for a three-dimensional spacetime map). This difference does not preclude representation of a light ellipse on a Minkowski diagram, as shown in Figures 2.6 and 2.7, corresponding, respectively, to the two interpretations of the Lorentz transformation offered by Poincaré before and after 1909.

In Poincaré’s pre-1909 interpretation of the Lorentz transformation, the radius vector of the light ellipse corresponds to light points at an instant of time as read by clocks at rest in the ether frame. The representation of this situation on a Minkowski diagram is that of an ellipse contained in a spacelike plane of constant time (Figure 2.6). The ellipse center coincides with spacetime point , and the points , , , and lie on the major axis, such that is a semi-minor axis of length . The light ellipse intersects the lightcone in two points, corresponding to the endpoints of the minor axis, and . There are no moving clocks in this reading, only measuring rods in motion with respect to the ether. (The -axis is suppressed in Figure 2.6 for clarity). The abstract nature of Poincaré’s early interpretation of the light ellipse is apparent in the Minkowskian representation, in that there are points on the light ellipse that lie outside the lightcone, and are physically inaccessible to an observer at rest in the ether.
In Poincaré’s post-1909 repurposing of the light ellipse, the light pulse is measured with comoving clocks, such that the corresponding figure on a Minkowski diagram is an ellipse in a plane of constant time . The latter -plane intersects the lightcone at an oblique angle, as shown in Figure 2.7, such that their intersection is a Poincaré light ellipse. (The -axis and the -axis are suppressed for clarity).
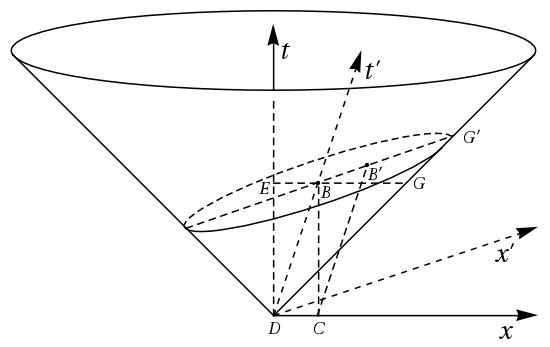
Both before and after 1909, Poincaré found that a spherical light pulse in the ether would be described as a prolate ellipsoid in inertial frames. Meanwhile, for Einstein and others who admitted the spatio-temporal relativity of inertial frames, the form of a spherical light pulse remained spherical in all inertial frames. In Poincaré’s scheme of things, only for ether-fixed observers measuring wavefronts with clocks and rods at rest is the light pulse a sphere; in all other inertial frames the light pulse is necessarily shaped like a prolate ellipsoid.
Comparison of Poincaré’s pre-1909 and post-1909 readings of the light ellipse shows the ellipse dimensions to be unchanged. What differs in the Minkowskian representations of these two readings is the angle of the spacelike plane containing the light ellipse with respect to the lightcone. The complementary representation is obtained in either case by rotating the light ellipse through an angle about the line parallel to the -axis passing through point .
We are now in a position to answer the question raised above, concerning the reasons for Poincaré’s embrace of time deformation in 1909. From the standpoint of experiment, there was no pressing need to recognize time dilation in 1909, although in 1907 Einstein figured it would be seen as a transverse Doppler effect in the spectrum of canal rays [9]. On the theoretical side, Minkowski’s spacetime theory was instrumental in convincing leading ether-theorists like Sommerfeld and Max Abraham of the advantages of Einstein’s theory. Taken in historical context, Poincaré’s poignant acknowledgment in Göttingen of time deformation (and subsequent repurposing of his light ellipse) reflects the growing appreciation among scientists, circa 1909, of the Einstein-Minkowski theory of relativity [53].
Bibliography
- [1] O. Blumenthal (Ed.) (1913) Das Relativitätsprinzip; Eine Sammlung von Abhandlungen. Teubner, Leipzig. link1 Cited by: §2.3.
- [2] (1914) Besprechung von Max Weinstein, Die Physik der bewegten Materie und die Relativitätstheorie. Physikalische Zeitschrift 15, pp. 676. Cited by: §2.2.
- [3] (1985) The institutional revolution in German physics, 1865-1914. Historical Studies in the Physical Sciences 15, pp. 1–65. Cited by: §2.2.
- [4] (2004) David Hilbert and the Axiomatization of Physics (1898–1918): From Grundlagen der Geometrie to Grundlagen der Physik. Kluwer, Dordrecht. Cited by: §2.2.
- [5] (1967) A History of Vector Analysis: The Evolution of the Idea of a Vectorial System. University of Notre Dame Press, South Bend. Cited by: §2.1.
- [6] (2012) Poincaré and light. See Poincaré, 1912–2012, Duplantier, Séminaire Poincaré, Vol. 16, pp. 1–43. Cited by: §2.1.
- [7] B. Duplantier (Ed.) (2012) Poincaré, 1912–2012. École polytechnique, Palaiseau. Cited by: 6.
- [8] (1905) Zur Elektrodynamik bewegter Körper. Annalen der Physik 322, pp. 891–921. link1 Cited by: §2.1, §2.1.
- [9] (1907) Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips. Annalen der Physik 328, pp. 197–198. Cited by: §2.3.
- [10] (1909) Die Stellung des Relativitätsprinzips im System der Mechanik und der Elektrodynamik. Sitzungsberichte der kaiserlichen Akademie der Wissenschaften, mathematisch-naturwissenschaftliche Classe IIa 118, pp. 373–446. link1 Cited by: §2.2.
- [11] (1979) Minkowski’s spacetime: from visual thinking to the absolute world. Historical Studies in the Physical Sciences 10, pp. 85–121. Cited by: §2.2, §2.3.
- [12] H. Goenner, J. Renn, T. Sauer, and J. Ritter (Eds.) (1999) The Expanding Worlds of General Relativity. Birkhäuser, Boston/Basel. Cited by: 46.
- [13] S. J. Gould (Ed.) (2001) The Value of Science: Essential Writings of Henri Poincaré. Random House, New York. Cited by: §2.1, §2.2.
- [14] J. Gray and S. A. Walter (Eds.) (1997) Henri Poincaré: Trois suppléments sur la découverte des fonctions fuchsiennes. Akademie-Verlag, Berlin. link1 Cited by: §2.1.
- [15] J. Gray (Ed.) (1999) The Symbolic Universe: Geometry and Physics, 1890–1930. Oxford University Press, Oxford. Cited by: 47.
- [16] M. Heidelberger and G. Schiemann (Eds.) (2009) The Significance of the Hypothetical in the Natural Sciences. Walter de Gruyter, Berlin. Cited by: 51.
- [17] (1884) Vorträge und Reden, Volume 1. Vieweg, Braunschweig. link1 Cited by: §2.2.
- [18] (1986) Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein, Volume 1: The Torch of Mathematics, 1800–1870. University of Chicago Press, Chicago. Cited by: §2.2.
- [19] (1986) Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein, Volume 2: The Now Mighty Theoretical Physics, 1870–1925. University of Chicago Press, Chicago. Cited by: §2.2.
- [20] M. J. Klein, A. J. Kox, and R. Schulmann (Eds.) (1993) The Collected Papers of Albert Einstein, Volume 5, The Swiss Years: Correspondence, 1902–1914. Princeton University Press, Princeton. link1 Cited by: §2.2.
- [21] (1893) Vorlesungen über continuierliche Gruppen mit geometrischen und anderen Anwendungen. Teubner, Leipzig. link1 Cited by: §2.1.
- [22] (1904) Electromagnetic phenomena in a system moving with any velocity less than that of light. Proceedings of the Section of Sciences, Koninklijke Akademie van Wetenschappen te Amsterdam 6, pp. 809–831. link1 Cited by: §2.1.
- [23] (1906) Sugli integrali delle equazioni dell’ elettrodinamica. Atti della R. Accademia dei Lincei, Rendiconti della Classe di scienze fisiche, matematiche e naturali 15, pp. 344–349. Cited by: §2.1.
- [24] (1981) Albert Einstein’s Special Theory of Relativity: Emergence (1905) and Early Interpretation. Addison-Wesley, Reading, MA. Cited by: §2.2.
- [25] (1896) Geometrie der Zahlen. Teubner, Leipzig. Cited by: §2.2.
- [26] (1908) Die Grundgleichungen für die electromagnetischen Vorgänge in bewegten Körpern. Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, pp. 53–111. link1 Cited by: §2.2, §2.2.
- [27] (1909) Raum und Zeit. Jahresbericht der deutschen Mathematiker-Vereinigung 18, pp. 75–88. link1 Cited by: Figure 2.3, Figure 2.5, Introduction.
- [28] (1915) Das Relativitätsprinzip. Jahresbericht der deutschen Mathematiker-Vereinigung 24, pp. 372–382. Cited by: §2.2, §2.2, §2.2, §2.2.
- [29] V. Petkov (Ed.) (2010) Minkowski Spacetime: A Hundred Years Later. Springer, Berlin. link1, link2 Cited by: 52.
- [30] (1907) Zur Dynamik bewegter Systeme. Sitzungsberichte der königliche preußischen Akademie der Wissenschaften, pp. 542–570. Cited by: §2.2.
- [31] (1906) Sur la dynamique de l’électron. Rendiconti del Circolo matematico di Palermo 21, pp. 129–176. link1, link2 Cited by: §2.1.
- [32] (1908) L’avenir des mathématiques. Revue générale des sciences pures et appliquées 19, pp. 930–939. link1 Cited by: §2.1.
- [33] (1909) La mécanique nouvelle. Revue scientifique 47-2 (6), pp. 170–177. link1 Cited by: §2.1.
- [34] (1910) Sechs Vorträge über ausgewählte Gegenstände aus der reinen Mathematik und mathematischen Physik. Teubner, Leipzig/Berlin. link1 Cited by: §2.1.
- [35] (1979) Physics in the shadow of mathematics: the Göttingen electron-theory seminar of 1905. Archive for History of Exact Sciences 21 (1), pp. 55–89. link1 Cited by: §2.2.
- [36] J. Renn and M. Schemmel (Eds.) (2007) The Genesis of General Relativity, Volume 3: Theories of Gravitation in the Twilight of Classical Physics, Between Mechanics, Field Theory, and Astronomy. Springer, Berlin. link1, link2 Cited by: 48.
- [37] (1993) Hyperbolic geometry on a hyperboloid. American Mathematical Monthly 100, pp. 442–455. Cited by: §2.2.
- [38] (1986) ‘Jewish mathematics’ at Göttingen in the era of Felix Klein. Isis 77, pp. 422–449. link1 Cited by: §2.2.
- [39] (2009) A look back at Hermann Minkowski’s Cologne lecture ‘Raum und Zeit’. Mathematical Intelligencer 31 (2), pp. 27–39. Cited by: §2.3.
- [40] (1991) Räumliche Anschauung und Minima positiv definiter quadratischer Formen. Jahresbericht der deutschen Mathematiker-Vereinigung 93, pp. 49–105. Cited by: §2.2.
- [41] (1909) Über die Zusammensetzung der Geschwindigkeiten in der Relativtheorie. Physikalische Zeitschrift 10, pp. 826–829. Cited by: §2.2.
- [42] J. Stachel, D. C. Cassidy, J. Renn, and R. Schulmann (Eds.) (1989) The Collected Papers of Albert Einstein, Volume 2, The Swiss Years: Writings, 1900–1909. Princeton University Press, Princeton. link1 Cited by: §2.2, 43.
- [43] (1989) Einstein and Laub on the electrodynamics of moving media. See The Collected Papers of Albert Einstein, Volume 2, The Swiss Years: Writings, 1900–1909, Stachel et al., pp. 503–507. Cited by: §2.2.
- [44] (1910) Anwendung der Lobatschefskijschen Geometrie in der Relativtheorie. Physikalische Zeitschrift 11, pp. 93–96. Cited by: §2.2.
- [45] (1997) La vérité en géométrie : sur le rejet mathématique de la doctrine conventionnaliste. Philosophia Scientiæ 2 (3), pp. 103–135. link1 Cited by: §2.2.
- [46] (1999) Minkowski, mathematicians, and the mathematical theory of relativity. See The Expanding Worlds of General Relativity, Goenner et al., Einstein Studies, Vol. 7, pp. 45–86. link1 Cited by: §2.3.
- [47] (1999) The non-Euclidean style of Minkowskian relativity. See The Symbolic Universe: Geometry and Physics, 1890–1930, Gray, pp. 91–127. link1 Cited by: §2.2.
- [48] (2007) Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910. See The Genesis of General Relativity, Volume 3: Theories of Gravitation in the Twilight of Classical Physics, Between Mechanics, Field Theory, and Astronomy, Renn and Schemmel, pp. 193–252. link1, link2 Cited by: §2.1, §2.2, §2.2.
- [49] S. A. Walter (Ed.) (2007) La correspondance d’Henri Poincaré, Volume 2: La correspondance entre Henri Poincaré et les physiciens, chimistes et ingénieurs. Birkhäuser, Basel. link1, link2 Cited by: §2.1.
- [50] (2008) Hermann Minkowski’s approach to physics. Mathematische Semesterberichte 55 (2), pp. 213–235. link1, link2 Cited by: §2.2, §2.2.
- [51] (2009) Hypothesis and convention in Poincaré’s defense of Galilei spacetime. See The Significance of the Hypothetical in the Natural Sciences, Heidelberger and Schiemann, pp. 193–219. link1 Cited by: §2.1, §2.2.
- [52] (2010) Minkowski’s modern world. See Minkowski Spacetime: A Hundred Years Later, Petkov, Fundamental Theories of Physics, Vol. 165, pp. 43–61. link1, link2 Cited by: §2.2.
- [53] (2014) Poincaré on clocks in motion. Studies in History and Philosophy of Modern Physics 47 (1), pp. 131–141. link1, link2 Cited by: §2.3.